半导体参数分析仪的FFT分析

 概述 

傅立叶分析可以将时域信号与频域信号进行转换。快速傅立叶变换（FFT）计算在获取时间相关的直流信号（如电流、电压）并将其转换为频率和基于交流的参数，如电流谱密度、1/f噪声、热噪声和交流阻抗）时非常有用。源测量单元 （SMU）和脉冲测量单元（PMU）是4200A-SCS参数分析仪的模块，用于在时域测量和加载输出电流或电压。仪器对这些基于时间的测量可以通过FFT计算转换为频域的参数。

从Clarius+ V1.9软件发布开始，4200A-SCS参数分析仪加载了FFT分析功能，能够自动对时域测量进行基于频率的计算，而无需下载数据并在单独的工具中执行分析。并且能够更快地获得重要的测试结果。本文给出了这些功能的说明以及FFT参数提取的一些典型案例，包括使用SMU和PMU进行电流谱密度测量，电阻热噪声测量以及RC电路的交流阻抗计算。

Clarius公式编辑器中的FFT相关功能

Clarius软件有一个内置的公式编辑器，能够对测试数据和其他计算结果进行数据计算。公式编辑器提供了各种计算函数、常用数学运算符和常用常量。从Clarius V1.9版本开始，FFT公式已添加到编辑器中。图1显示了带有FFT的函数编辑器的截图。

图1. 在Clarius软件的函数编辑器中的FFT功能

表1列出了内置的FFT函数及其描述。这些方程对输入数组的实部和虚部行FFT变换或FFT逆变换，然后获得对应的输出实部或虚部分量。其中两个公式从输入时间数组返回频率数组。平滑函数通过将高频分量归零，对输入数组进行数字滤波。

表1. FFT公式和描述

在使用FFT公式时，最好以均匀间隔的时间间隔获取数据。当将时间数组转换为频率数组时，FFT_Freq函数允许用户输入一个容差参数，以确定连续间隔的时间数据是否均匀间隔。如果输入时间数组中两点之间的差值（以百分比表示）大于容差值，则会将“#REF”返回到Sheet。

计算出的实部和虚部数据数组的输出数据量将是2的幂次方。因此,理想的采集数据点数应该是2的幂次方，比如64、128、256、512、1024等。如果数据点的数量不是2的幂次方，则返回的点数将被减少，使其等于2的幂次方。 

使用FFT测试示例

Clarius库中的多个测试，包含了使用FFT公式将基于时间的电流或电压测量转换为频率相关参数的示例。这些例子包括SMU电流谱密度、电阻器的热噪声、PMU电流谱密度和RC电路的交流阻抗。

SMU电流谱密度与频率测量

Clarius库中的SMU电流谱密度（smu-isd）测试，使用SMU进行的随时间变化的直流电流测量，从中得出电流谱密度与频率的相关函数。根据设备和应用的不同，该测试可能能够用于导出包括设备的电流噪声，1/f 噪声。

在本测试中，4201-SMU使用Normal速度模式，在三个不同的电流范围 (1mA，1µA和1nA) 下，测试开路的直流电流与时间关系。SMU的Force HI和Sense HI端子上需要加盖金属帽。FFT函数将会导出电流、功率、频率、带宽和电流谱密度的实分量和虚分量，如图2所示。

图2. smu-isd 测试公式

三次测试运行得到的电流谱密度与频率曲线如图3所示。因为测量的是用开路的电流，所以基本上是推导出来的是SMU的本底噪声。频率会根据定时设置而发生变化。

这些图表显示的是电流噪声谱密度，以 A/sqrt(Hz) 为单位，而不是以单次，安培为单位，直流测量的噪声。从快速傅立叶变换的数学表达式来看，电流频谱密度在这里定义为：

    ISD = sqrt(2*PWR/(PTS*BW))

其中，

    PWR是电流幅度的平方，或者PWR= Im(I)^2 + Re(I)^2

    BW是时间采样的带宽

    PTS是点数，它应该是2的幂次方

带宽 (BW) 定义为1/dt，其中dt为两次测量之间的时间间隔，假设所有测量之间的时间间隔为恒定值。

图3. SMU不同档位的电流谱密度与频率

测量速度在测试设置窗口中配置。虽然不能直接设置测量时间间隔，但测量时间、带宽和测试频率都是已知的，并会返回到列表中。在设置speed模式时，通常需要在每个单次直流测量的速度和噪声之间进行权衡。测量速度越快，噪声就越大。对于总测试时间较长的测量，带宽较小，因此噪声也较小。

本测试中的测量是在固定的电流量程上进行的。使用固定量程，而不是自动量程，这对于保持每个读数的测量时间恒定是非常重要的，这是FFT计算所需要的。

之所以使用sampling测试模式，是因为加载了一个恒定的偏置。在该模式下，必须输入读数的个数。尽管在使用FFT计算时需要大量的读数，但这并不实用。

在这个测试中，读取了1024个读数，因为1024是2的幂次方。表2列出了SMU电流谱密度测试的公式。

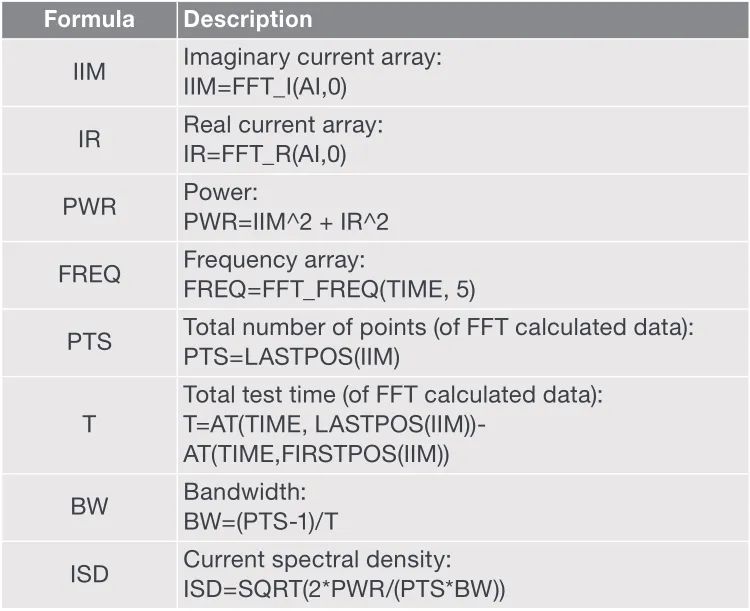
表2. SMU电流谱密度测试公式

电阻的热噪声

电阻的热噪声或约翰逊噪声可以通过电阻上的直流电压与时间的测量来计算。测试库中的resistor-noise测试项测量0A的直流电压与时间的函数，并计算在1GΩ电阻上的实部和虚部的电压数组、功率、频率、带宽和电压谱密度。电阻于SMU1和GNDU之间。一旦执行测试，热噪声（VSD）被绘制为频率的函数，如图4所示。

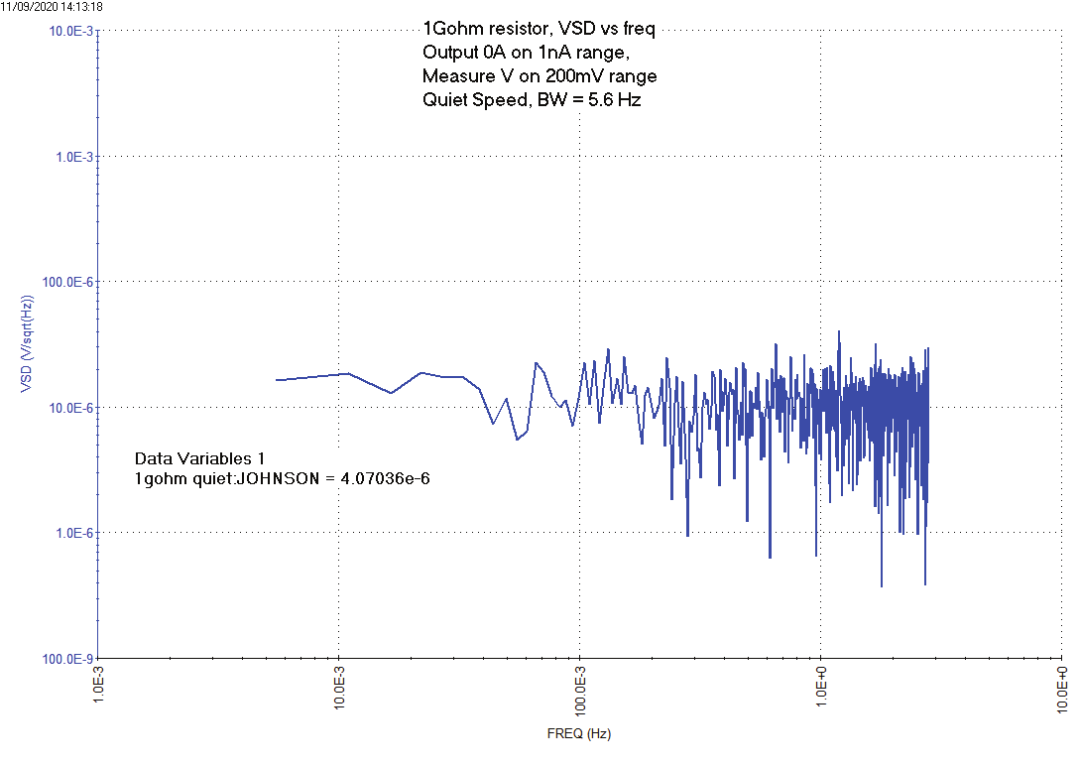
图4. 1GΩ电阻的热噪声

在这个测试中，直流电压测量是在200mV 量程上进行的，在1nA量程上施加0A。计算1GΩ电阻的噪声电流和约翰逊噪声。1GΩ电阻的热噪声理论计算值约为4E-6Vrms，使用公式：vn=sqrt(4*k*TEMP* 1e9)。

电阻器热功率噪声的实际公式为：

    P=4*k*TEMP*BW

其中，

    k为玻尔兹曼常数，1.38 E-23 J/K

    TEMP为环境温度 (K)

    BW为带宽 (Hz)

表3列出了resistor-noise测试的公式描述。时间、量程、点数和其他设置的信息与导出SMU电流谱密度的描述类似。

表3. 电阻热噪声测试相关公式

使用PMU获取电流谱密度

和SMU一样，4225-PMU的电流谱密度也可以通过电流和时间的测量以及FFT计算得出。在测试库中可以找到pmu-isd，在100μA和100nA范围内测试计算 PMU 开路的电流谱密度。这个测试是通过使用PMU_freq_time_ulib用户库中的PMU_sampleRate用户模块生成的。使用PMU测试，我们可以在CH1和CH2上加载电压偏置，选择CH2的电流范围，并指定总测试时间和采样率。pmmu-isd测试的配置如图5所示。

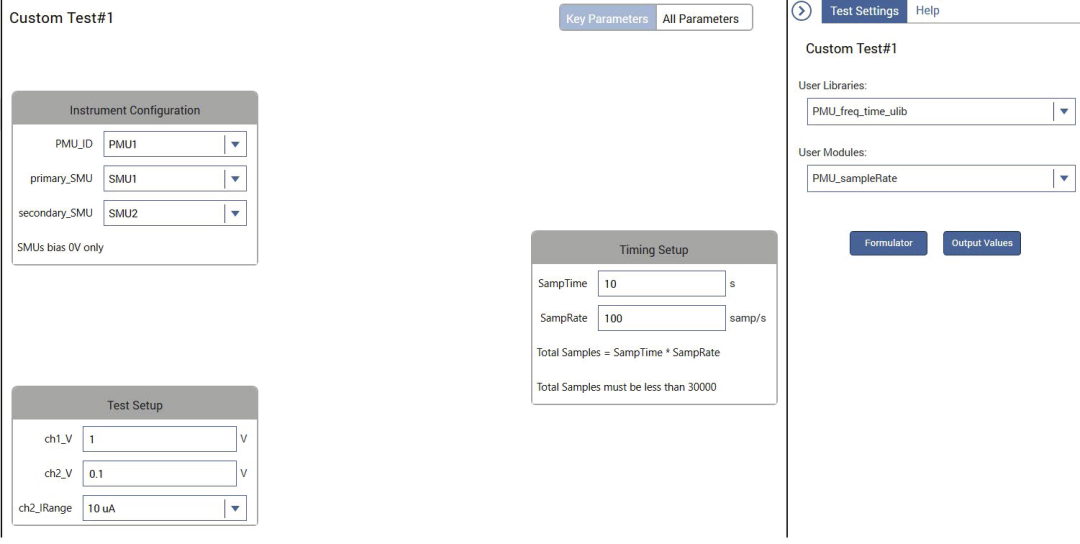
图5. pmu-isd测试配置视图

与 SMU 电流谱密度测试一样，公式编辑器有几个公式可以推导出测试电流的带宽、实部分量和虚部分量、功率、频率和电流谱密度。图6显示了100µA和100nA档位下电流谱密度与频率的函数曲线。由于数据是用开路采集的，因此这些是在固定电流量程上以可选采样率测量到的PMU本底噪声。

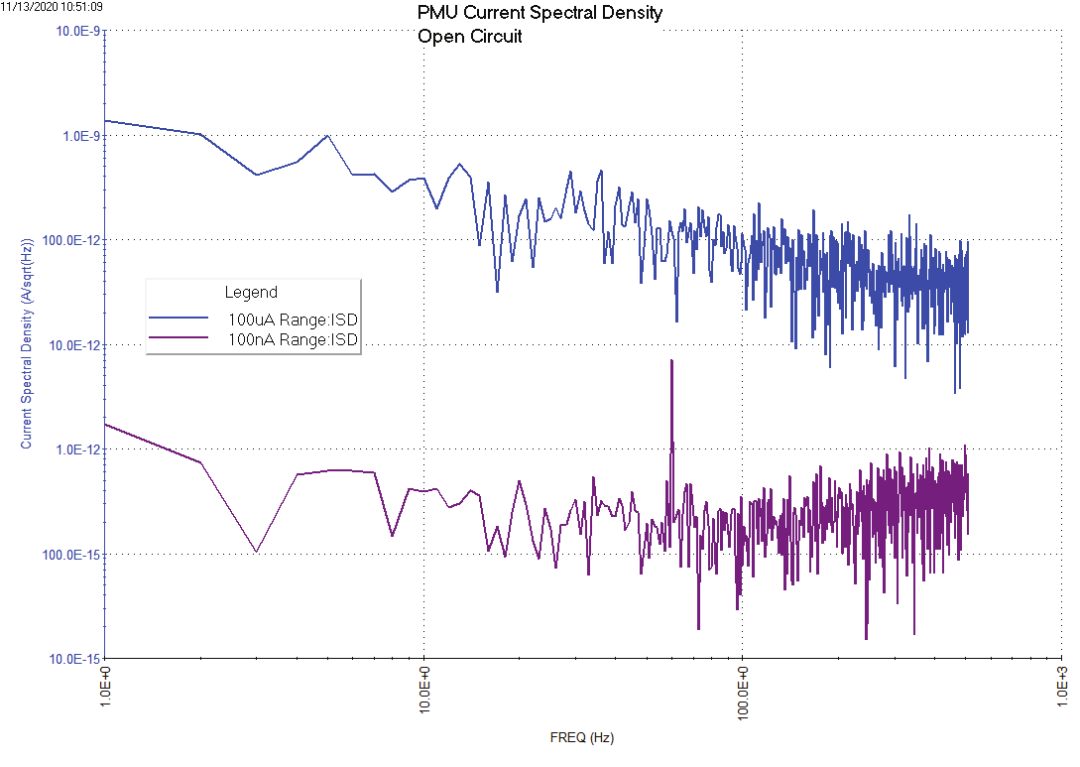
图6. PMU电流谱密度

在configure视图中，输入总测试时间和采样率。点数等于总测试时间乘以采样率。选择输入参数，由于将对数据执行FFT计算，使点数总数为2的幕次方。为了获得最佳的结果，至少应该使用20个点或更多。对于本次测试，带宽设置为1024HZ。

表4. PMU谱密度测试相关公式

 

测定RC串联电路的交流阻抗

使用双通道4225-PMU结合内置的FFT计算公式，可以提取RC电路的AC阻抗参数。PMU在时域测量电流和电压，Clarius公式编辑器中的FFT通过计算将这些测试结果转换为频域的相关参数。

例如，可以在PMU的CH1和CH2之间连接串联 RC电路，如图7所示。CH1输出周期性脉冲波形 (ACV)，CH2测量产生的电流 (imeas)。通过 FFT 计算得到测试电路的AC阻抗参数，如串联电阻(Rs)和电抗 (Xs)，以及阻抗的实部和虚部。电容(Cs)和耗散因子(D)可以用Rs和Xs推导出来。

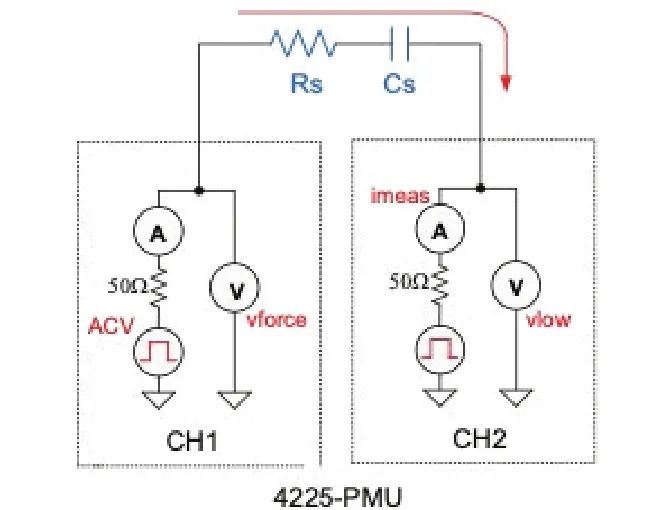
图7. 用于测量串联RC电路AC阻抗的PMU连接

R-C Circuit AC Impedance Calculations (rs-cs-ac-

impedance) 测试项，包含RC串联电路的AC参数。在这个测试示例中，PMU的CH1输出一个具有指定幅度和测试频率的脉冲波形。还指定了周期数和每个周期上的测试点数。在公式编辑器中配置计算，以提取100kΩ，10nF，R-C串联电路的AC阻抗参数。此测试的配置如图8所示。

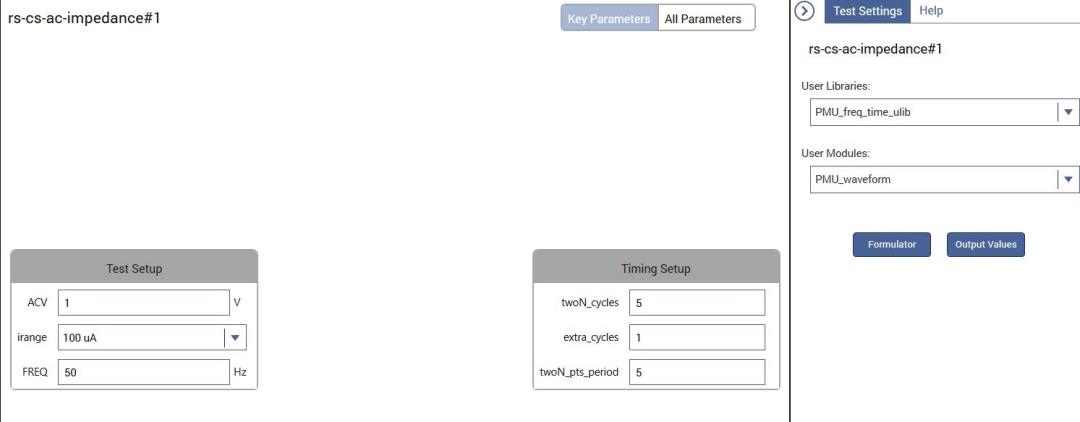
图8. rs-cs-ac-impedance测试的配置视图

在此测试中，在配置视图中输入CH1的电压脉冲幅值 (ACV)、CH2的电流测量范围 (irange)、测试频率 (FREQ)、2^n个周期和2^n个点。表5列出了本次测试的输入参数。基于这些输入参数，PMU构建具有电流测量值的电压段波形。

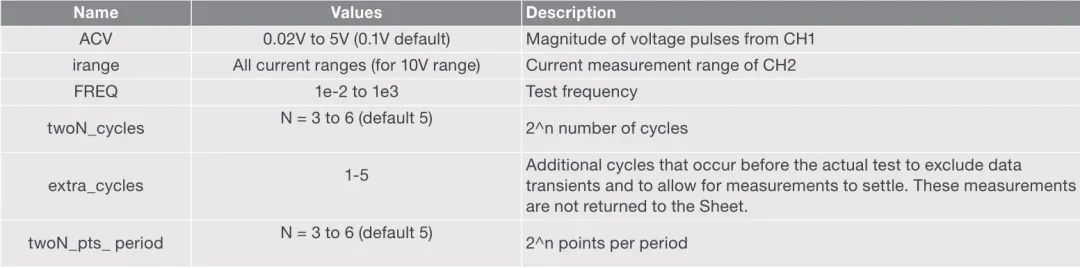
表5. rs-cs-ac-immpedance测试输入参数

在对周期信号进行FFT计算时，通常需要大量的周期然而，获取大量数据通常是不现实的。为了确保足够的精度，至少需要测试32(2^5)个周期，每个周期有32(2^5)个数据点。在rs-cs-ac-impedance测试中,周期数和每个周期的点数都是 32。

如果想同时提取串联电阻(RS)和电容(Cs)，最好选择近似为：F=1/RC的测试频率。不过，这可能需要些实验。通常在测量电容或电阻之间需要进行权衡。更精确的电容测量需要更小的系数D，D<0.1，而更精确的电阻测量需要更高的系数D，D>1。当需要足够的精度提取同时获取RS和Cs时，选择F=1/RC提供了一个权衡方案。

一旦执行测试，返回到 Sheet相等的点数可以通过以下公式计算:

每次测试的总点数=循环次数 x 每个循环的点数

对于本次测试，总点数=32x32=1024。CH1上的测量脉冲电压(vforce)，CH2的电压(vlow)，时间和 CH2上的测量电流(imeas)的数组返回到表中。输出参数的描述参考在表6。

表6. rs-cs-ac-impedance测试输出参数

从返回值中，可以提取许多AC参数。对于本次测试，RC串联电路的所有计算参数如表7所示。

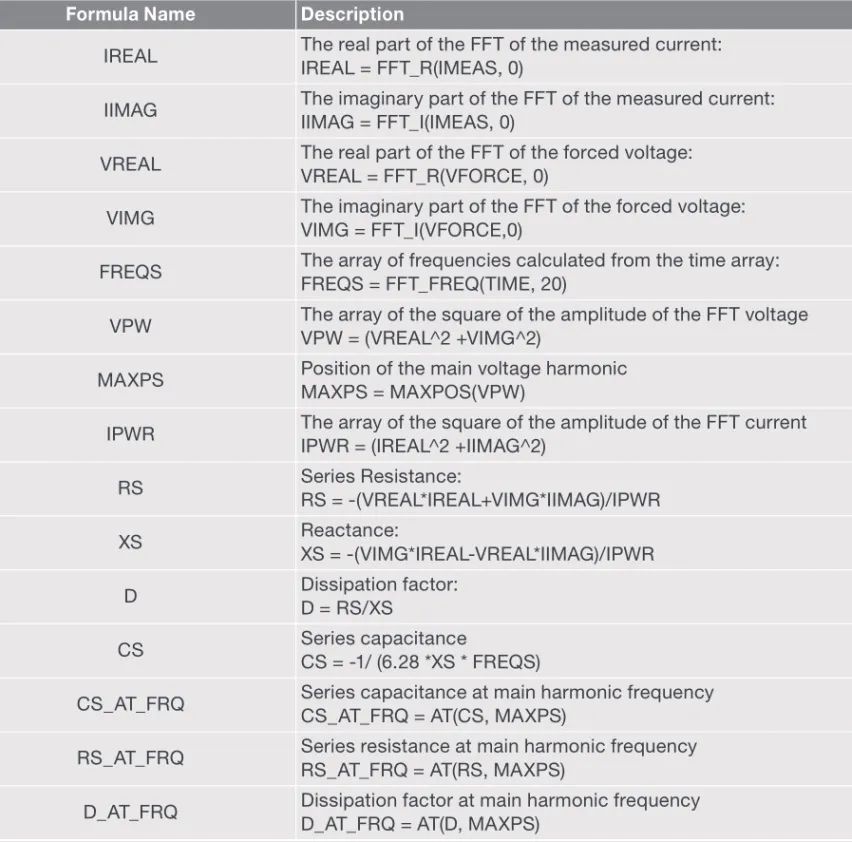
表7. 计算参数

所有输出和计算参数也返回到列表中，并在Analyze视图中绘制图形，如图9所示。数据可以在时域和频域上绘制。左图为电压和电流随时间变化的函数曲线。右图为电压 (VPWR) 和电流 (IPWR) 幅值的平方的数组与频率的函数曲线。导出主谐波频率处的Cs、Rs和D，并出现在表格的最后三列中。

图9. 将数据在时域和频域进行绘制

rs-cs-ac-impedance测试项使用PMU_freq_time_ulib用户库中的pmu_waveform用户模块。此用户模块还可用于执行其他需要的特定测试频率脉冲波形的测试。

结论

4200A-SCS参数分析仪对直流电流和电压测量执行FFT计算的能力使许多AC参数的提取成为可能，包括电流谱密度、热噪声和AC阻抗。这使得我们能够更快地获得测试结果，因为不再需要单独的工具来执行FFT分析。

将您的灵感变为现实

我们提供专业的测量洞见信息，旨在帮助您提高绩效以及将各种可能性转化为现实。
泰克设计和制造能够帮助您测试和测量各种解决方案，从而突破复杂性的层层壁垒，加快您的全局创新步伐。我们携手共进，一定能够帮助各级工程师更方便、更快速、更准确地创造和实现技术进步。