晶体单元基础知识

晶体单元

 

1.振动模式和方向角

关于AT切割的振动模式，图1显示了室温附近频率-温度特性的主要系数达到零的方向角

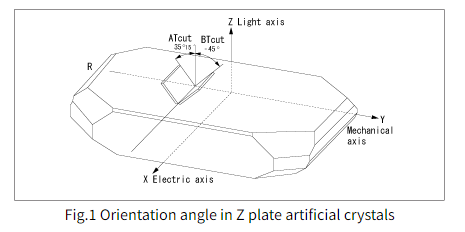
厚度剪切振动模式如图2所示

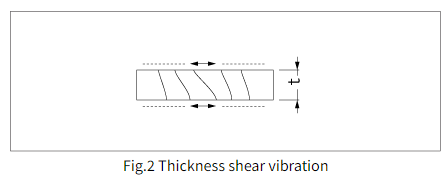
对于常用的AT切割晶体，其频率范围和频率系数（晶体板厚度与振荡频率之间的关系）如表1所示。

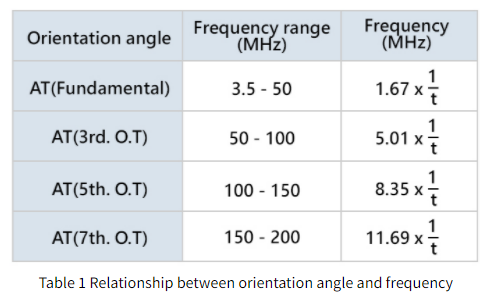
2.频率温度特性

晶体的频率-温度特性根据其曲线形状分为两类。一个是三次曲线，另一个是二次曲线。AT切割的典型频率温度特性分别如图3和图4所示。AT切割晶体单元被最广泛地使用，因为它们在室温范围内对温度变化的响应产生较小的频率变化。

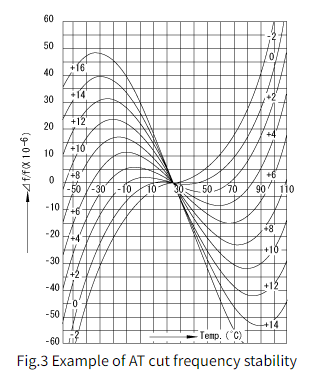
3.等效电路和各种常数

石英晶体在谐振频率附近的等效电路如图5所示。

R1：串联电阻

L1：运动电感

C1：运动电容

C0：分流电容

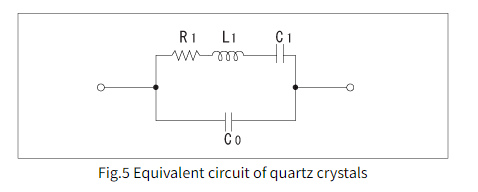
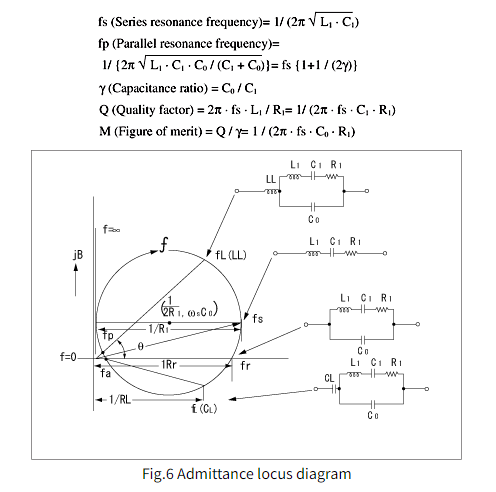
图6显示了晶体单元在其振荡频率附近的导纳轨迹图和晶体单元的等效电路。该图显示了各种电路条件下等效电路的配置以及振荡频率与电阻之间的关系等。在这里，我们可以发现各种常数之间的以下关系

石英晶体振荡电路

1.典型振荡电路（基本振荡模式）

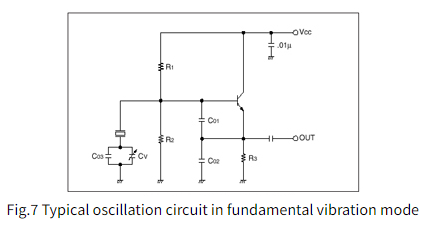
典型的振荡电路图如图7所示。

当振荡模式处于稳态时，晶体单元Xe的电抗、电路电抗-X、晶体Re的阻抗和电路阻抗-R之间的关系如下：

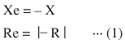
稳态下的简化振荡电路如图8所示。

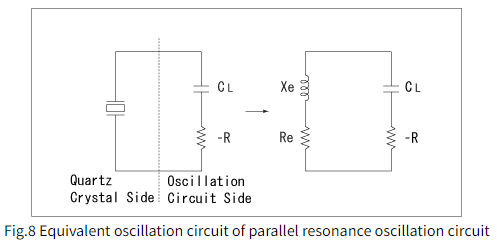
为了获得电路的安全振荡，电路的负电阻必须满足以下方程：-R|>Re。

以图7中的电路为例，电路的负电阻如下

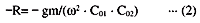
在这里，

gm=晶体管在振荡阶段的互导

ω（=2π·f）=振荡角频率

 

2.负载电容和振荡频率

鉴于此

串联谐振频率=fr

等效串联电容=C1

并联电容=C0

谐振频率（带负载电容CL）=fL

fL-fr=deltaf

那么，

 

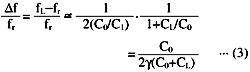
推导出了上述方程式。

负载电容可以看作C01的串联电容，

C02和C03+CV，如图7所示，包括晶体管的杂散电容和电路图案。

因此，负载电容CL由以下方程式给出。

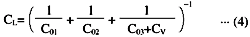
当振荡电路的负载电容可以从CL1改变到CL2时的频率变化范围“牵引范围”表示为，

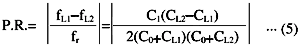
如果给定等效串联电容C1、并联电容C0以及上述CL1和CL2，则可以从上述方程中得出频率变化范围。“牵引灵敏度”，即负载电容（CL）附近元件的灵敏度，由以下方程式给出。

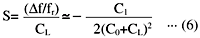
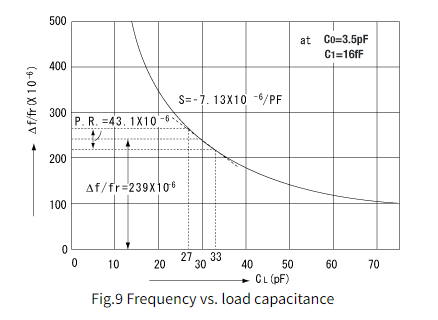
谐振频率与负载电容特性如图9所示。上述方程式（3）、（5）、（6）的计算结果

在C1=16fF、C0=3.5pF、CL=30pF、CL1=27pF和CL2=33pF的给定条件下。

通过应用这种现象，可以通过调整可变微调电容器来抵消由于晶体单元的生产偏差和振荡电路中组件的偏差而导致的偏差，从而将振荡电路的输出频率微调到标称频率。

虽然方程式（6）中负载电容（CL）的减小将提高器件灵敏度，但反过来也会降低稳定性。

请注意，负载电容的减小将增加启动振荡的难度，因为晶体单元的有效电阻将增加，如方程式（7）所示。

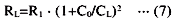
3.晶体振荡器的驱动电平

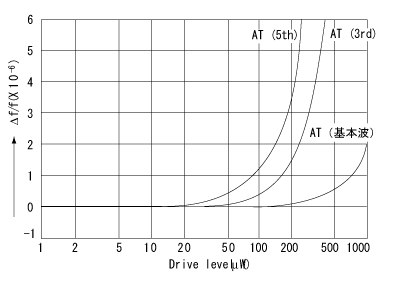
为了保证晶体振荡器的稳定振荡，必须施加一定程度的驱动功率。图13显示了频率如何随驱动水平而变化，频率偏移量随着驱动水平的增加而增加。

向晶体单元施加高驱动功率（约50mW）会对其造成损坏。在正常振荡电路中使用时，

优选的驱动功率为0.1mW或更小（最大0.5mW）。

4.设计PCB图案时必须考虑以下几点。

从振荡级到晶体单元的图案长度应最小，以将振荡回路的杂散电容保持在最小值。

当将其他组件和布线图案放在振荡回路上时，应将杂散容量的增加保持在最低限度。