

如何由阻尼比求闭环极点和增益
描述
在自动控制系统中,阻尼比、闭环极点和增益是三个至关重要的参数,它们共同决定了系统的稳定性和动态性能。
一、阻尼比的定义与意义
阻尼比(Damping Ratio),通常表示为ξ(xi),是描述系统阻尼特性的一个重要参数。它反映了系统阻尼器对系统振动的抑制能力,即系统振动的衰减速度。阻尼比越大,系统振动的衰减速度越快,系统的稳定性越好;反之,阻尼比越小,系统振动的衰减速度越慢,系统的稳定性越差。
在二阶系统中,阻尼比ξ与自然频率ω_n一起决定了系统的动态响应特性。二阶系统的传递函数可以表示为:
其中,K是系统增益,s是复频率变量,ω_n是系统的自然频率。从这个传递函数中,我们可以看出系统的动态性能与阻尼比ξ、自然频率ω_n以及增益K密切相关。
二、闭环极点的求解
闭环极点是系统闭环传递函数分母为零时的根,它们决定了系统的稳定性和动态响应。在自动控制系统中,通常需要通过调整闭环极点的位置来优化系统的性能。
对于二阶系统,其闭环传递函数可以表示为: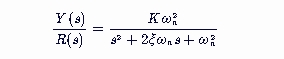
其中,Y(s)是输出信号的拉普拉斯变换,R(s)是输入信号的拉普拉斯变换。闭环极点是该传递函数分母为零时的解,即求解方程: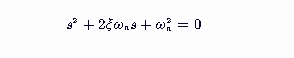
的根。
这个方程是一个二次方程,其解为: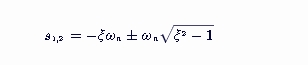
这两个解就是系统的闭环极点。根据阻尼比ξ的不同取值,闭环极点的性质也会有所不同:
- 过阻尼系统(ξ > 1) :此时,方程的两个解都是实数,且均为负值。系统响应将按照指数形式单调逐渐稳定到输入,无振荡现象。
- 临界阻尼系统(ξ = 1) :此时,方程的两个解重合,为一个实数。系统响应同样将按照指数形式单调逐渐稳定到输入,但比过阻尼系统响应更快。
- 欠阻尼系统(0 < ξ < 1) :此时,方程的两个解为一对共轭复数。系统响应为衰减振荡曲线,且逐渐稳定到输入。系统的衰减程度和振荡程度分别由闭环极点的实部和虚部决定。
三、增益的求解与调整
增益K是系统对输入信号的放大倍数,它决定了系统输出的幅值大小。在自动控制系统中,增益的选择对系统的稳定性和动态性能有着重要影响。
对于给定的阻尼比ξ和自然频率ω_n,增益K的选择需要根据系统的具体要求进行。一般来说,可以通过以下步骤来求解和调整增益:
- 确定系统要求 :首先,需要明确系统对稳定性、响应速度和稳态误差等性能指标的要求。
- 选择阻尼比ξ :根据系统要求,选择合适的阻尼比ξ。如果系统需要快速响应且无振荡,可以选择较小的阻尼比;如果系统需要较好的稳定性,可以选择较大的阻尼比。
- 计算闭环极点 :根据选定的阻尼比ξ和自然频率ω_n,计算闭环极点的位置。
- 调整增益K :在保持闭环极点位置不变的情况下,通过调整增益K来满足系统对输出幅值的要求。需要注意的是,增益K的调整可能会影响到系统的稳定性和动态性能,因此需要谨慎进行。
- 仿真验证 :在完成增益K的调整后,需要进行仿真验证以检查系统的性能是否满足要求。如果不满足要求,需要重新调整阻尼比ξ和增益K。
声明:本文内容及配图由入驻作者撰写或者入驻合作网站授权转载。文章观点仅代表作者本人,不代表电子发烧友网立场。文章及其配图仅供工程师学习之用,如有内容侵权或者其他违规问题,请联系本站处理。
举报投诉
-
如何去理解增益带宽积 、开环运放带宽、闭环系统的带宽这几个参数?2024-08-12 1019
-
闭环增益对系统动态性能的影响2024-07-30 4634
-
过阻尼系统的动态性能指标有哪些2024-07-29 3717
-
请问用在单位增益的闭环负反馈中的op-amp阻尼大不大?2021-06-25 1761
-
温度和风速对桥梁结构模态频率和阻尼比的影响研究2021-04-25 1040
-
运放开环增益、闭环增益和环路增益详解2020-12-15 5762
-
风电系统弱阻尼低频振荡模式抑制2018-03-14 1574
-
数字陷波器有源阻尼方法2018-03-13 1429
-
多变量阻尼比灵敏度的有功调制2017-12-14 1196
-
开环增益与闭环增益2017-11-24 111439
-
二阶闭环系统的频率特性曲线2009-05-15 3289
全部0条评论

快来发表一下你的评论吧 !

