

Vision Board 轻松完成【电赛E题】
描述
题目简述
一、 任务
设计并制作三子棋游戏装置,能够控制机械臂或其他机构放置棋子,实现人 机对弈。图 1 所示的三子棋棋盘和棋子位置示意图中,棋盘由黑色实线围成 9 个方格,人、机分别从棋子放置处拾取棋子并放置到方格中,先将己方的 3 个棋 子连成一线(横连、竖连、斜连皆可)即获胜。
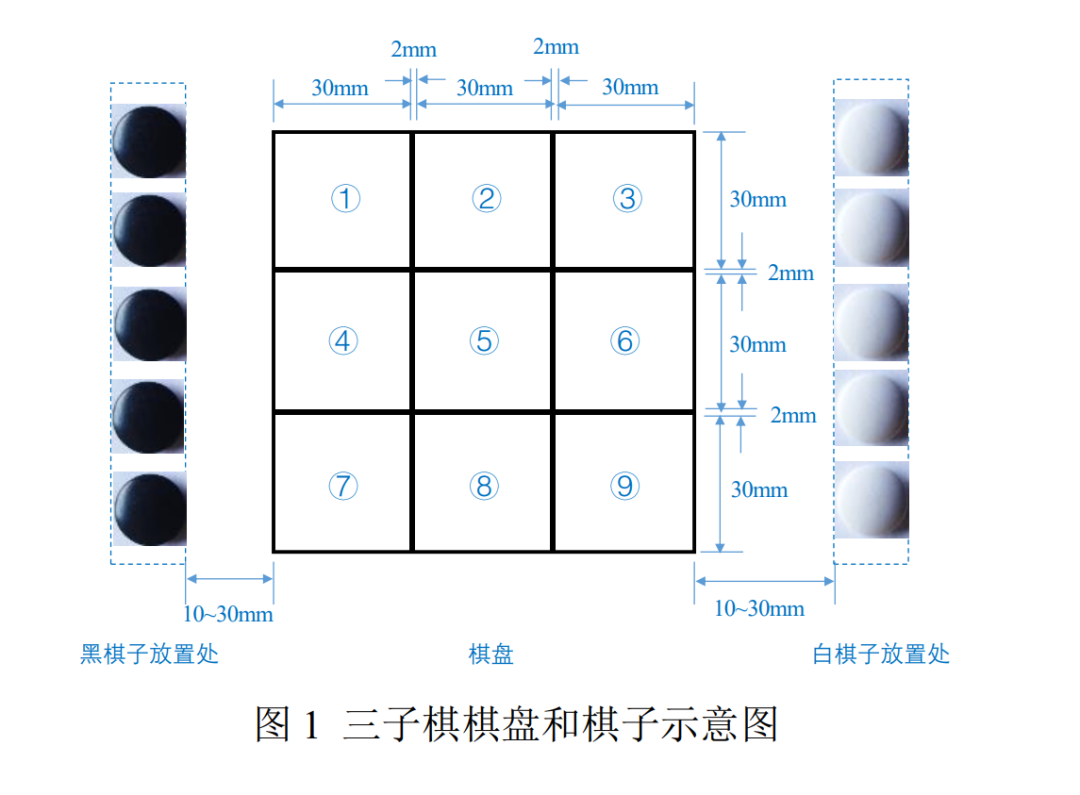
二、 要求
(1)装置能将任意 1 颗黑棋子放置到 5 号方格中。(5 分)
(2)装置能将任意 2 颗黑棋子和 2 颗白棋子依次放置到指定方格中。(20 分)
(3)将棋盘绕中心±45°范围内旋转后,装置能将任意 2 颗黑棋子和 2 颗 白棋子依次放置到指定方格中。(20 分)
(4)装置执黑棋先行与人对弈(第 1 步方格可设置),若人应对的第 1 步白 棋有错误,装置能获胜。(20 分)
(5)人执黑棋先行,装置能正确放置白棋子以保持不输棋。(20 分)
(6)对弈过程中,若人将装置下过的 1 颗棋子变动位置,装置能自动发现 并将该棋子放置回原来位置。(10 分)
Vision Broad开发板简述
开发板描述:Vision Board搭载全球首颗 480 MHz Arm Cortex-M85芯片,拥有Helium和TrustZone技术的加持。SDK包里集成了OpenMV机器视觉例程,配合MicroPython 解释器,使其可以流畅地开发机器视觉应用。Vision Board具有以下主要特点:
强大的处理性能:Vision Board搭载了全球首款基于 ARM Cortex-M85 架构的瑞萨电子RA8 MCU,6.39 CoreMark/MHz,可以快速而高效地运行机器视觉算法,实现图像处理、等功能。
完整支持OpenMV生态:Vision Board完全兼容OpenMV开发平台,用户可以直接使用OpenMV IDE进行编程和开发,利用丰富的API和库函数进行图像处理和计算机视觉任务。
友好的学习环境:提供简洁易用的开发环境和示例项目,带领初学者快速上手机器视觉、GUI等应用。同时具有丰富的文档资料供给开发者学习。
可扩展性:丰富的扩展接口,如摄像头、MIPI-DSI、RGB666、树莓派兼容IO、BTB拓展接口等,用户可以根据自己的需求连接其他外设或模块,如以太网、CAN/LIN、传感器、执行器等,实现更复杂的应用场景。
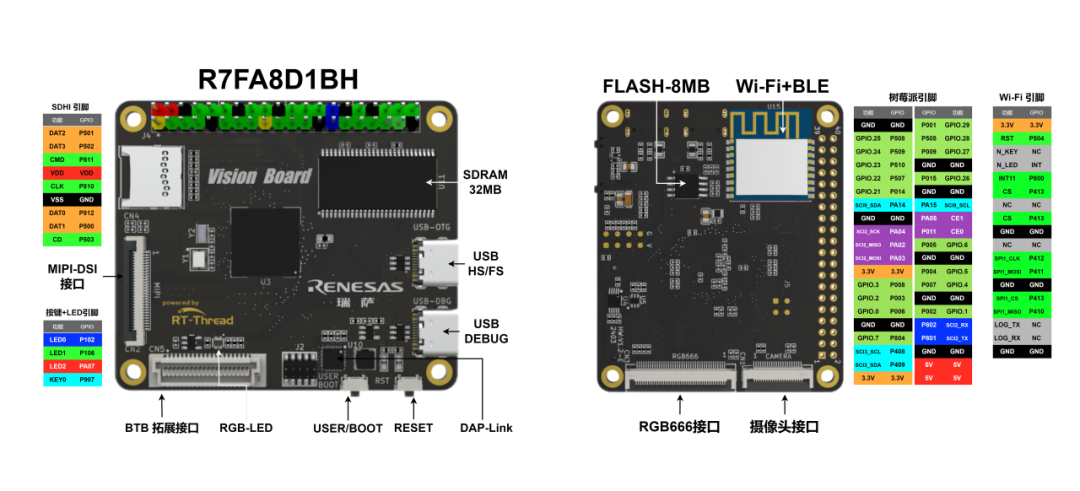
板载资源:
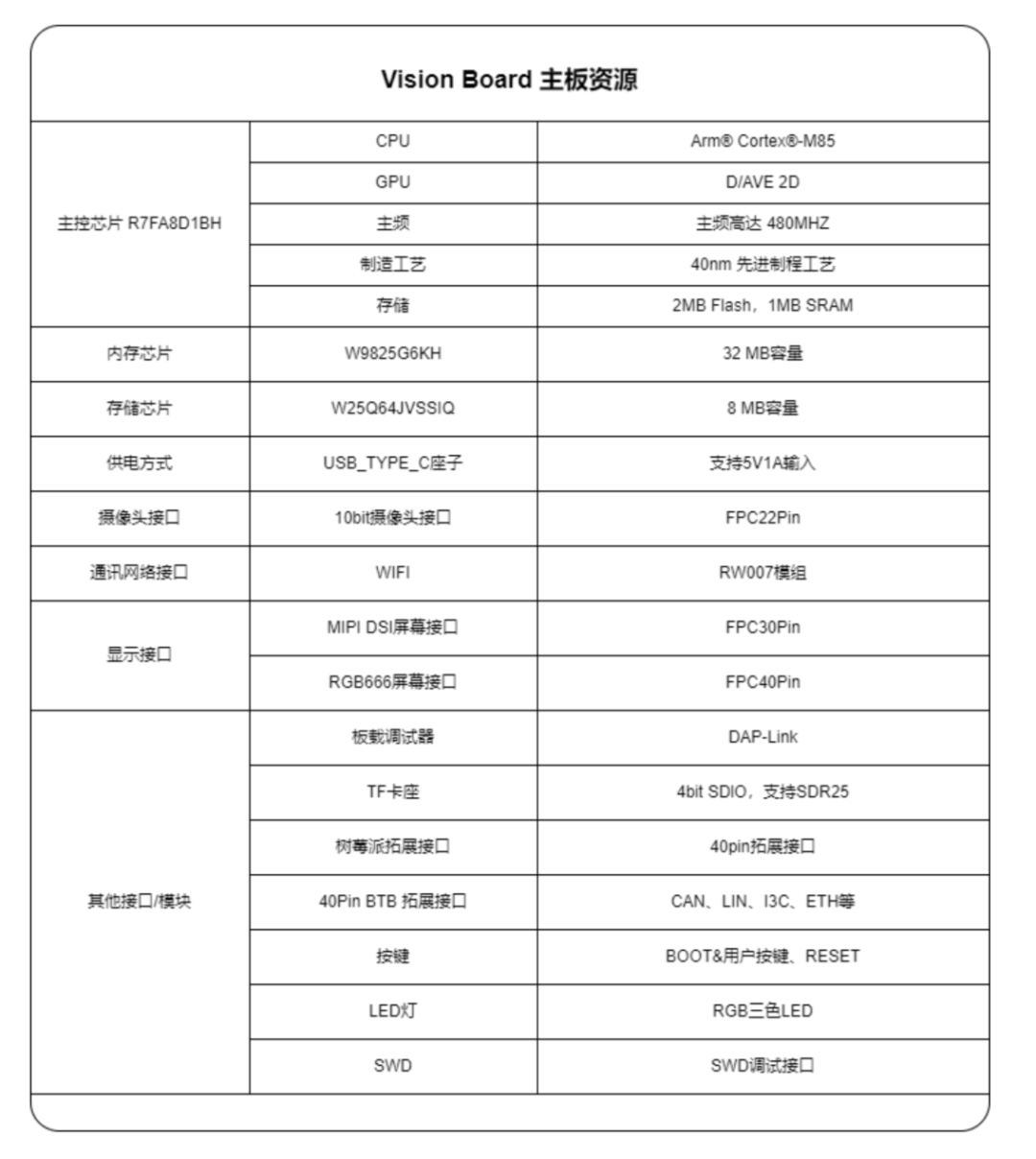
外设支持情况:

支持的 IDE:RT-Thread Studio、MDKV538。OpenMV工程目前仅支持MDK开发
三子棋思路
找棋盘
生成居中的九宫格区域
函数 generate_centered_rois 的目的是生成一个九宫格的区域,每个区域都包含棋盘上的一个方块,并且这些区域在整个图像中居中。函数的参数包括图像的宽度和高度、每个方块的边长 b 以及感兴趣区域(ROI)的边长 k。
函数定义
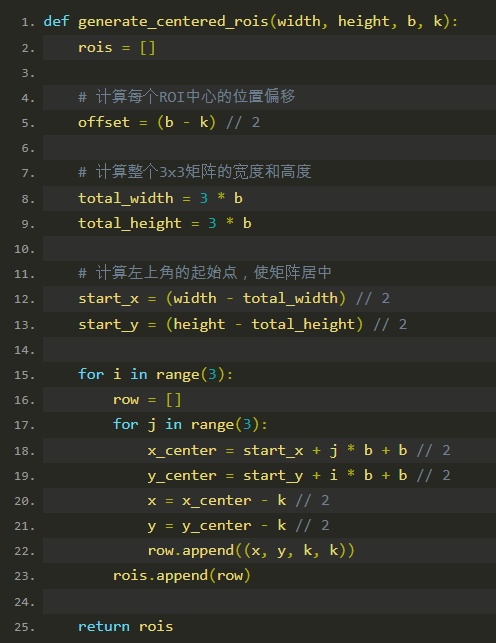
步骤解析
1.初始化区域列表:

rois 是一个列表,用于存储每个 ROI 的坐标和大小。
2.计算每个 ROI 中心的位置偏移:
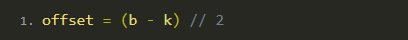
偏移量 offset 是为了确保 ROI 在每个方块的中心。b 是方块的边长,而 k 是 ROI 的边长。
3.计算整个九宫格的总宽度和高度:

因为九宫格有 3 行 3 列,每个方块的边长为 b,所以总宽度和高度分别是 3 * b。
4.计算左上角的起始点:

为了使九宫格在图像中居中,我们计算左上角的起始点 start_x 和 start_y。它们分别是图像宽度和高度减去九宫格的总宽度和高度的一半。
5.生成九宫格区域:
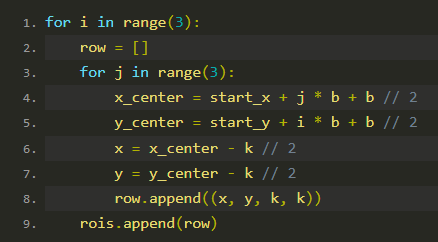
使用双重循环生成每个 ROI 的坐标。
x_center 和 y_center 计算每个方块的中心位置。
x 和 y 是 ROI 的左上角坐标,减去 k // 2 是为了将 ROI 的中心对齐到方块的中心。
最后,将每个 ROI 添加到 rois 列表中。
6.返回 ROI 列表:

视觉化解释
假设图像的宽度和高度分别为 320 和 240,每个方块的边长 b 为 43,每个 ROI 的边长 k 为 10。九宫格将会在图像中居中,每个 ROI 将位于方块的中心,形成一个规则的 3x3 矩阵。
找棋子
棋子识别的关键在于处理图像并根据灰度值来判断每个方块中是否存在棋子,以及棋子的颜色是黑色还是白色。这个过程在 while 循环中进行。
代码段
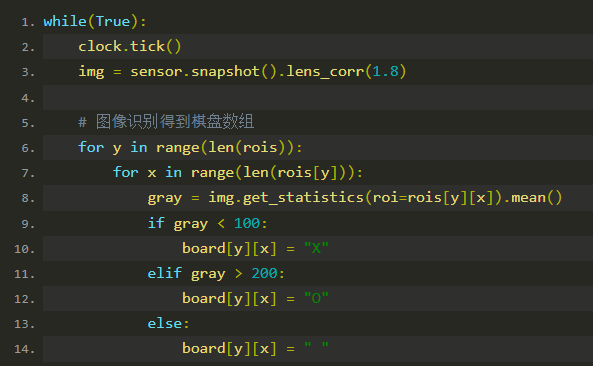
步骤解析
1.抓取图像和镜头矫正:

使用 Vision Broad的摄像头捕获当前图像,并进行镜头矫正,以减少镜头畸变。
2.遍历所有 ROI(感兴趣区域):

使用双重循环遍历之前生成的九宫格区域 rois。
3.计算灰度值的平均值:

对每个 ROI 计算灰度值的平均值。img.get_statistics(roi=rois[y][x]) 返回一个统计对象,包含了该 ROI 内的像素统计数据。通过 mean() 方法可以得到该区域的平均灰度值。
4.判断灰度值来确定棋子:
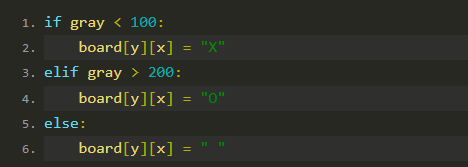
如果灰度值小于 100,则认为该区域有一个黑色棋子("X")。
如果灰度值大于 200,则认为该区域有一个白色棋子("O")。
否则,该区域为空(" ")。
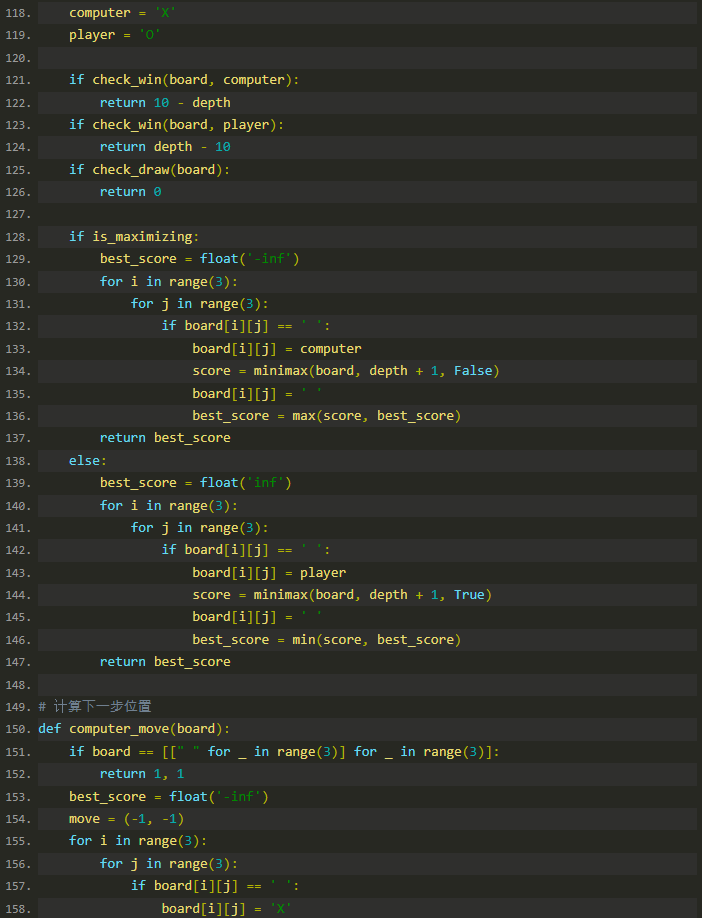
博弈策略计算
minimax 函数
minimax 函数使用递归的方法评估所有可能的棋步,并为每个棋步计算一个分数,以确定最佳移动。
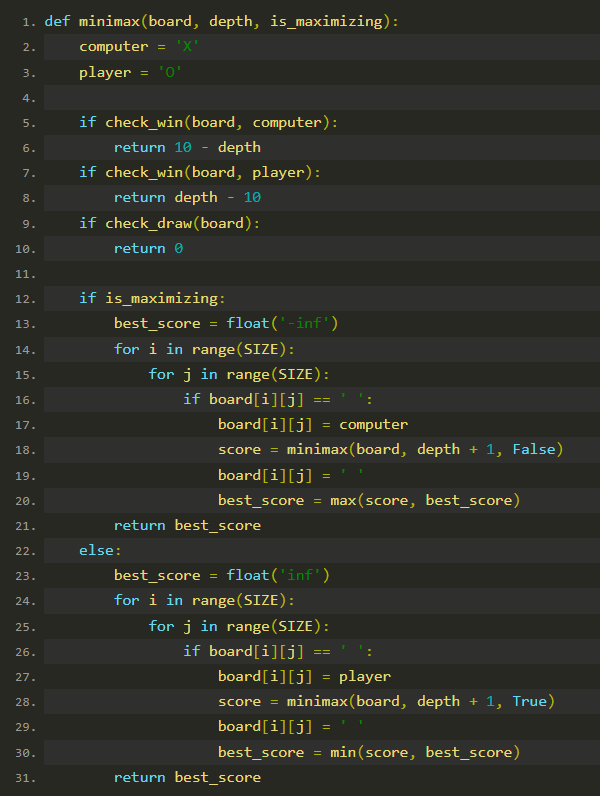
步骤解析
1.定义变量:

定义机器人棋子为 ‘X’,玩家棋子为 ‘O’。
2.检查终止条件:
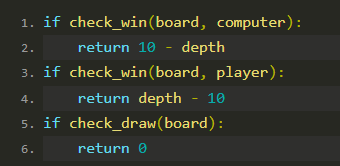
如果机器人赢了,返回一个正分(10 减去深度,越快赢分数越高)。
如果玩家赢了,返回一个负分(深度减去 10,越快输分数越低)。
如果平局,返回 0 分。
递归搜索:
机器人最大化得分:
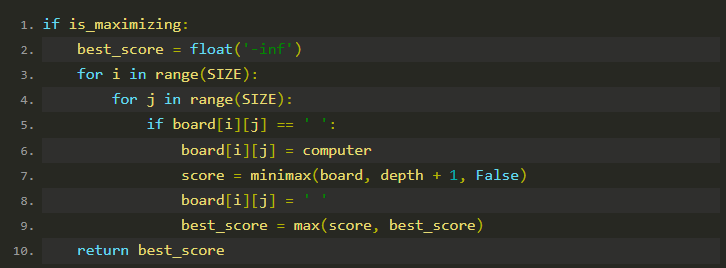
初始化 best_score 为负无穷。
遍历每个空位置,模拟机器人下棋。
递归调用 minimax 计算对方的最佳应对分数。
恢复棋盘状态,更新 best_score。
返回最佳分数。
玩家最小化得分:
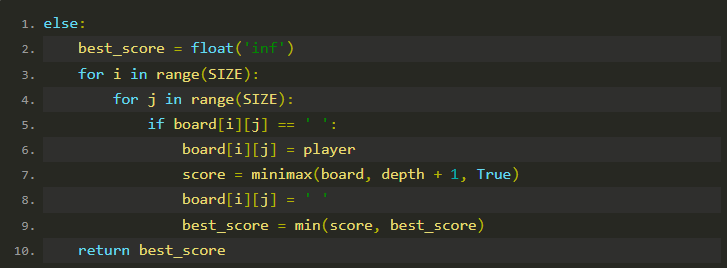
初始化 best_score 为正无穷。
遍历每个空位置,模拟玩家下棋。
递归调用 minimax 计算机器人的最佳应对分数。
恢复棋盘状态,更新 best_score。
返回最佳分数。
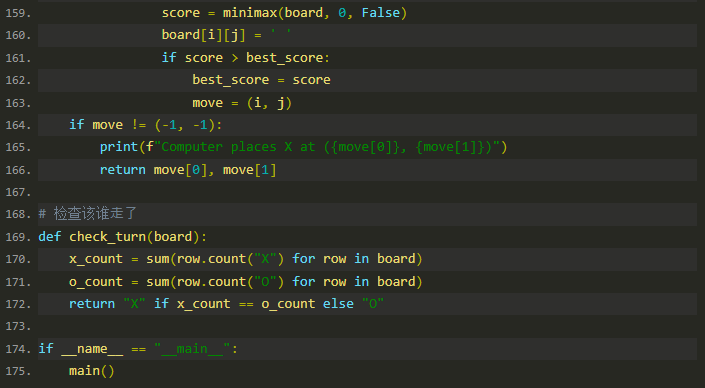
computer_move 函数
computer_move 函数用来确定机器人下一步应该下到哪里。
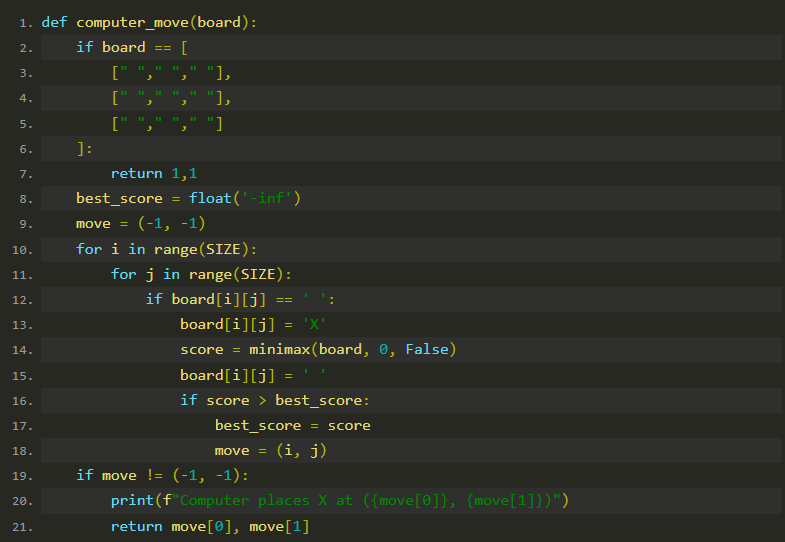
步骤解析
1.初始化变量:

初始化 best_score 为负无穷,用来追踪最佳分数。move 用来记录最佳移动位置。
2.遍历棋盘找空位:
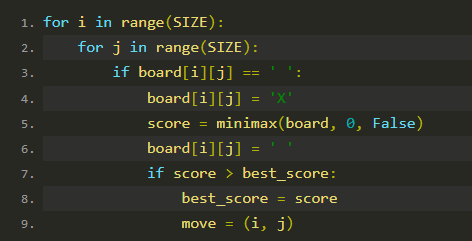
遍历每个位置,如果是空位,模拟机器人在此下棋。
调用 minimax 计算此移动的分数。
恢复棋盘状态。
如果当前移动的分数大于 best_score,更新 best_score 和 move。
3.返回最佳移动位置:

如果找到最佳移动位置,返回该位置的坐标。
总结
Minimax 算法:通过递归搜索所有可能的棋步,评估每个棋步的得分,最大化机器人的得分,最小化玩家的得分。
确定最佳移动:遍历所有可能的移动,调用 minimax 算法计算每个移动的得分,并选择得分最高的移动。
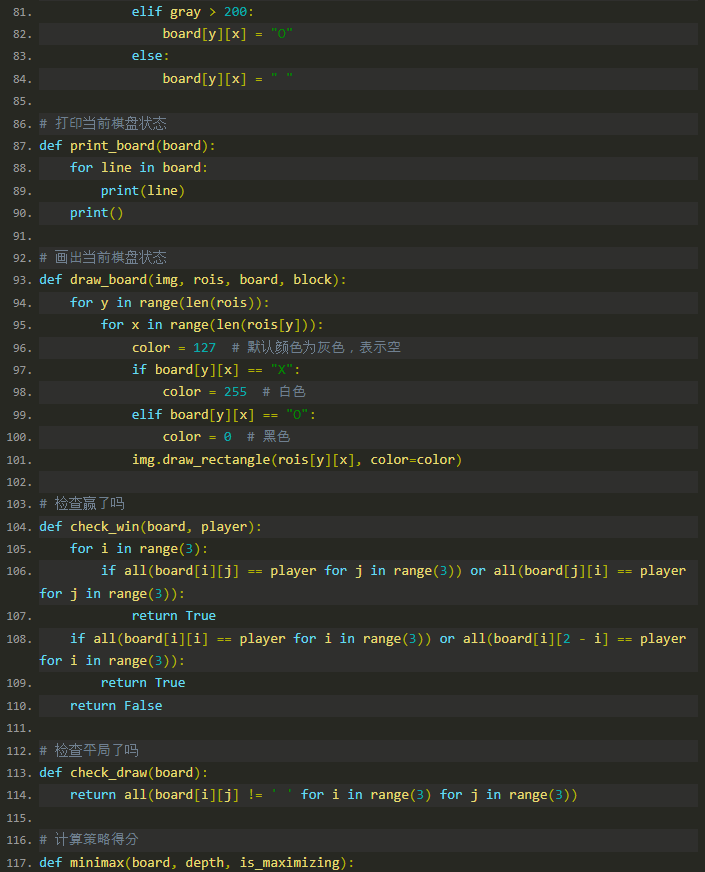
赢者检测
赢者检测是通过 check_win 函数实现的。该函数会检查棋盘的行、列和对角线,判断某个玩家是否已经获胜。
check_win 函数

步骤解析
1.检查行和列:

遍历每一行,检查该行是否全部是当前玩家的棋子。如果是,返回 True。
遍历每一列,检查该列是否全部是当前玩家的棋子。如果是,返回 True。
2.检查对角线:

检查主对角线(从左上到右下),是否全部是当前玩家的棋子。如果是,返回 True。
检查副对角线(从右上到左下),是否全部是当前玩家的棋子。如果是,返回 True。
3.未找到获胜者:

如果没有找到任何一行、一列或对角线全部是当前玩家的棋子,返回 False。

完整代码:
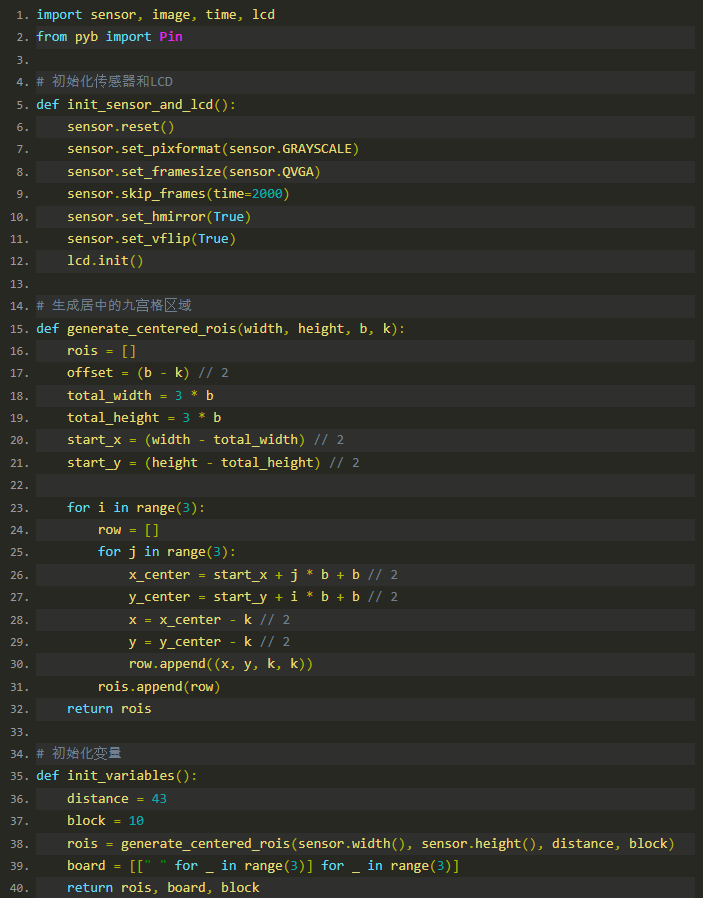
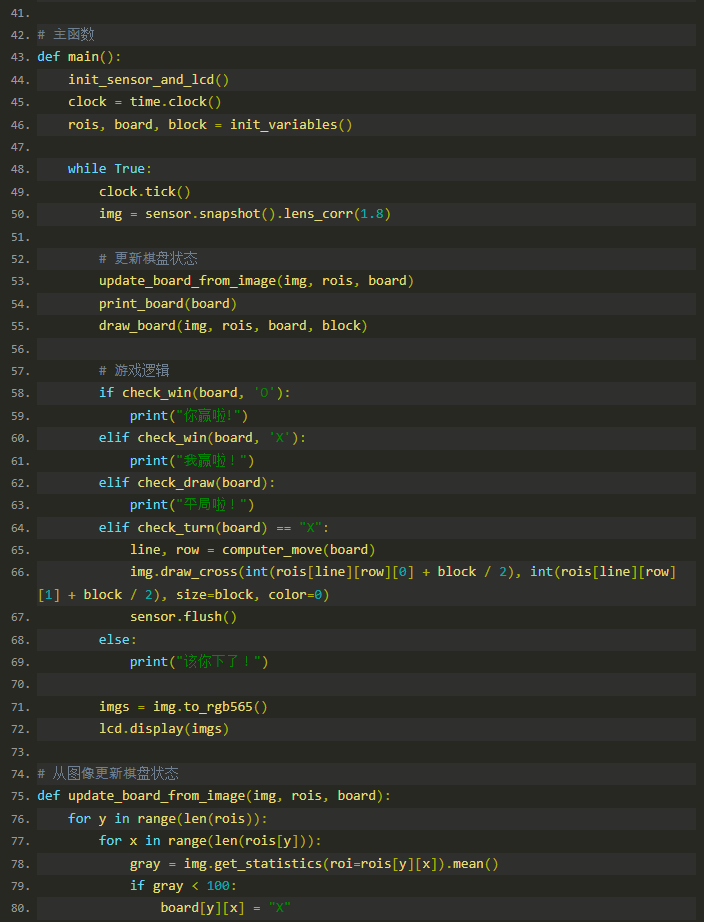
全部0条评论

快来发表一下你的评论吧 !

