LC谐振回路解析，LC谐振回路的选频特性

　　LC谐振回路是高频电路里最常用的无源网络， 包括并联回路和串联回路两种结构类型。 

　　利用LC谐振回路的幅频特性和相频特性，不仅可以进行选频，即从输入信号中选择出有用频率分量而抑制掉无用频率分量或噪声（例如在选频放大器和正弦波振荡器中），而且还可以进行信号的频幅转换和频相转换（例如在斜率鉴频和相位鉴频电路里）。另外，用L、 C元件还可以组成各种形式的阻抗变换电路和匹配电路。所以，LC谐振回路虽然结构简单，但是在高频电路里却是不可缺少的重要组成部分，在本书所介绍的各种功能的高频电路单元里几乎都离不开它。

　　LC并联谐振回路：

　　图1.21（a）是电感L、电容C和外加信号源Is组成的并联谐振回路。r是电感L的损耗电阻，电容的损耗一般可以忽略。 （b）图是其等效转换电路，ge0和Re0分别称为回路谐振电导和回路谐振电阻。 

　　根据电路分析基础知识， 可以直接给出LC并联谐振回路的某些主要参数及其表达式：

　　

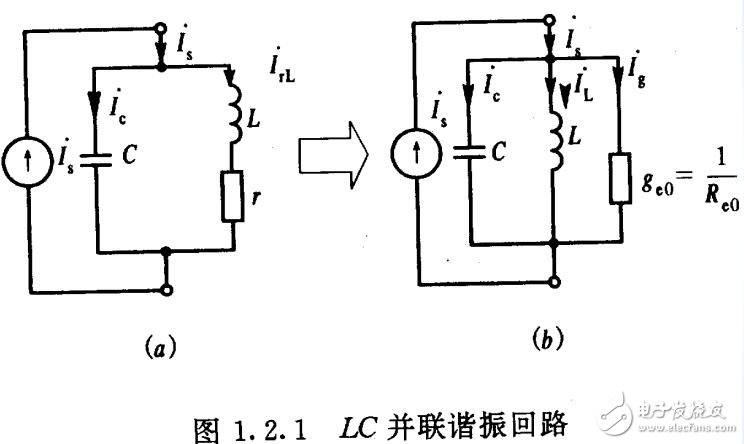
　　（1） 回路谐振电导

　　

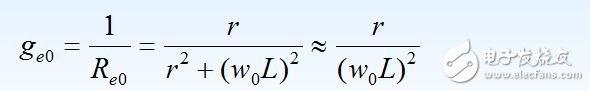
　　（2） 回路总导纳

　　

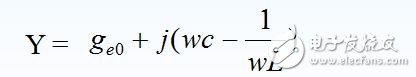
　　（3） 谐振频率

　　

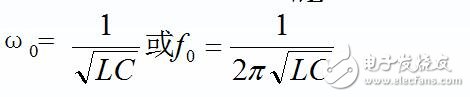
　　（4） 回路两端谐振电压

　　

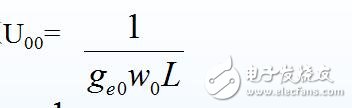
　　（5） 回路空载Q值

　　

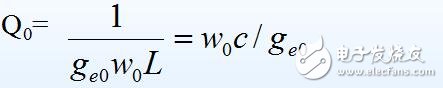
　　（6） 单位谐振曲线

　　谐振时，回路呈现纯电导，且谐振导纳最小（或谐振阻抗最大）。回路电压U与外加信号源频率之间的幅频特性曲线称为谐振曲线。谐振时，回路电压U00最大。任意频率下的回路电压U与谐振时回路电压U00之比称为单位谐振函数，用Ｎ（ｆ）表示。Ｎ（ｆ）曲线称为单位谐振曲线。

　　

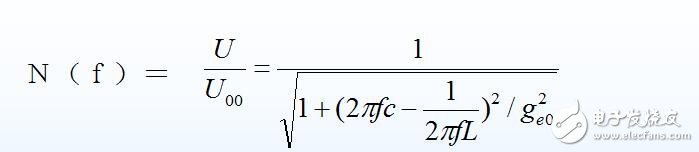
　　由Ｎ（ｆ）定义可知， 它的值总是小于或等于１。 

　　由式（１．２．３）和式（１．２．５）可得：

　　

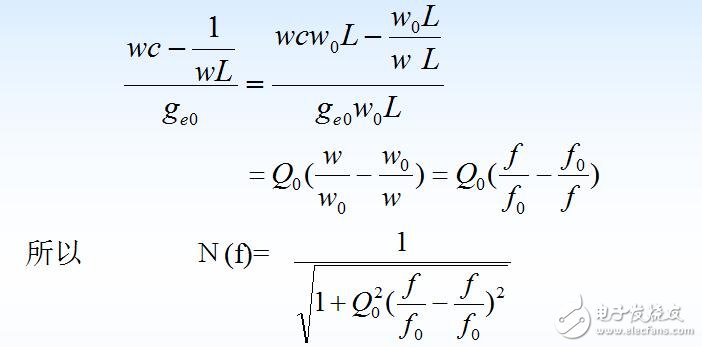
　　定义相对失谐

　　

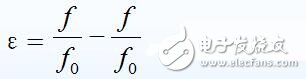
　　当失谐不大时，即ｆ与ｆ0相差很小时

　　

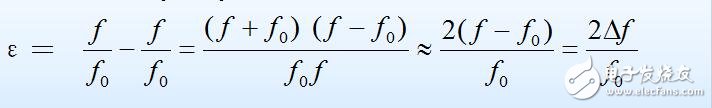
　　所以

　　

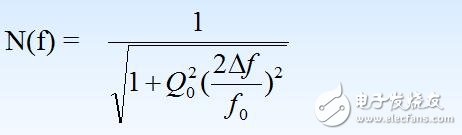
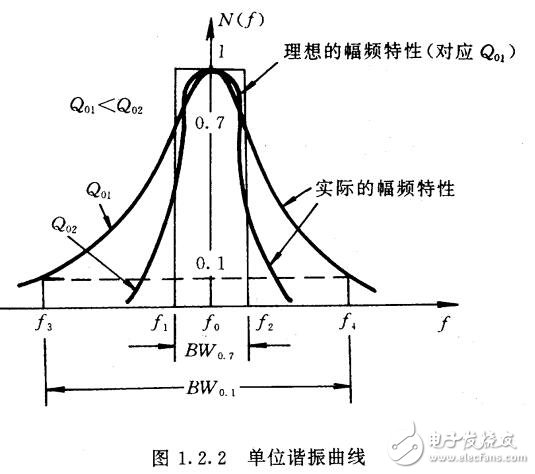
　　根据式（１．２．１０）可作出单位谐振曲线Ｎ（ｆ）。 该曲线如图１．２．２所示。

　　

　　（7） 通频带、选择性、矩形系数。

　　由图１．２．２可知，Ｑ0越大，谐振曲线越尖锐，选择性越好。 为了衡量回路对于不同频率信号的通过能力，定义单位谐振曲线上

　　

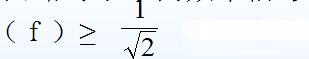
　　所包含的频率范围为回路的通频带， 用ＢＷ0.7表示。在图上ＢＷ0.7＝ｆ2－ｆ1，取?

　　

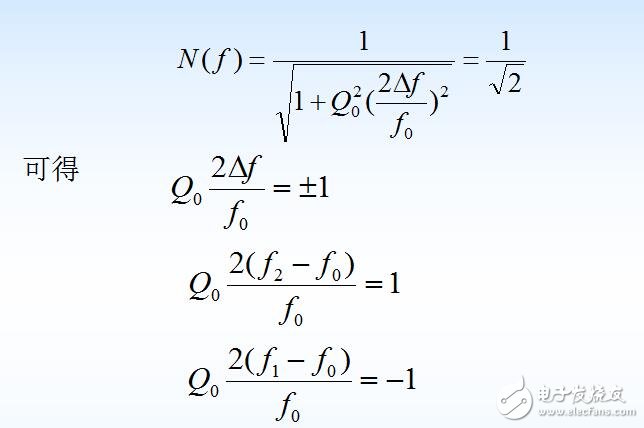
　　将式（１．２．１１）减去式（１．２．１２）， 可得到：

　　

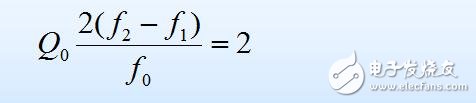
　　所以

　　

　　可见， 通频带与回路Ｑ值成反比。 也就是说， 通频带与回路Ｑ值（即选择性）是互相矛盾的两个性能指标。 选择性是指谐振回路对不需要信号的抑制能力， 即要求在通频带之外， 谐振曲线Ｎ（ｆ）应陡峭下降。所以，Ｑ值越高，谐振曲线越陡峭， 选择性越好，但通频带却越窄。一个理想的谐振回路， 其幅频特性曲线应该是通频带内完全平坦，信号可以无衰减通过，而在通频带以外则为零，信号完全通不过，如图１．２．２所示宽度为ＢＷ0.7、高度为１的矩形。

　　为了衡量实际幅频特性曲线接近理想幅频特性曲线的程度，提出了“矩形系数”这个性能指标。 ?

　　矩形系数Ｋ0.1定义为单位谐振曲线Ｎ（ｆ）值下降到０．１时的频带范围ＢＷ0.1与通频带ＢＷ0.7之比， 即：

　　

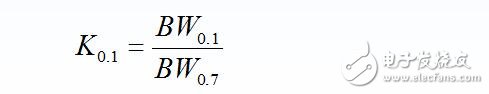
　　由定义可知，Ｋ01是一个大于或等于１的数， 其数值越小， 则对应的幅频特性越理想。

　　LC串联谐振回路：

　　图１．２．３是串联ＬＣ谐振回路的基本形式， 其中ｒ是电感Ｌ的损耗电阻，ＲL是负载电阻。

　　

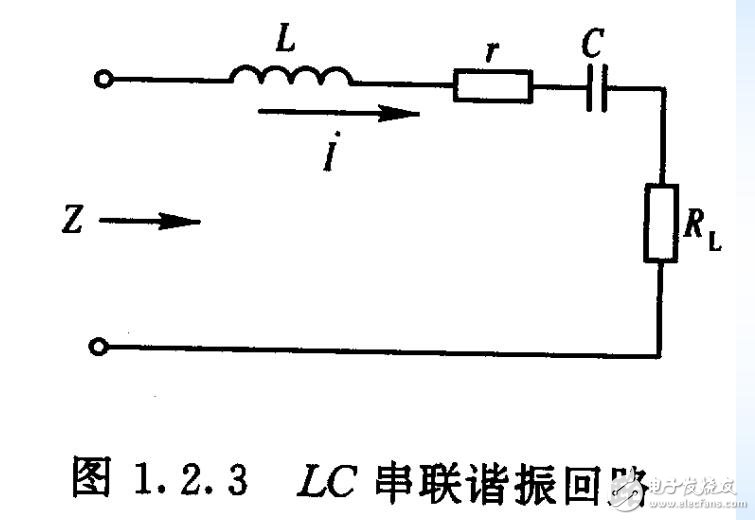
　　下面按照与并联ＬＣ回路的对偶关系， 直接给出串联ＬＣ回路的主要基本参数。

　　

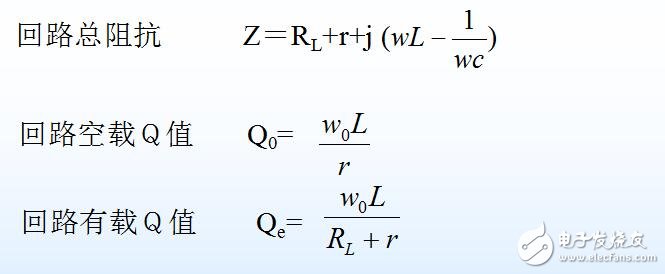
　　谐振频率

　　

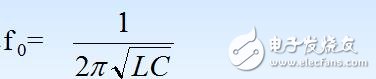
　　单位谐振函数

　　

　　

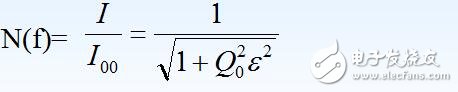
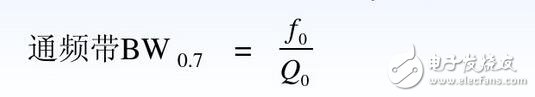
　　其中Ｉ是任意频率时的回路电流， Ｉ??00?是谐振时的回路电流。

　　串、 并联谐振回路阻抗特性比较：

　　串联谐振回路空载时阻抗的幅频特性和相频特性表达式分别为：

　　

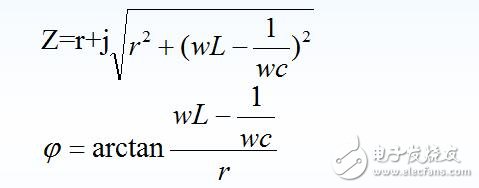
　　并联谐振回路空载时阻抗的幅频特性和相频特性表达式分别为：

　　

　　

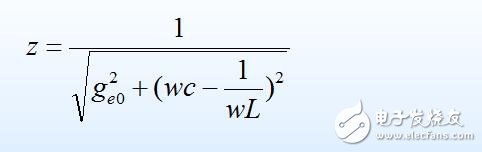
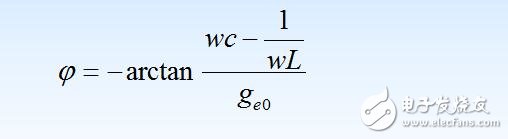
　　图１．２．４（ａ）、 （ｂ）分别是串联谐振回路与并联谐振回路空载时的阻抗特性曲线。由图可见，前者在谐振频率点的阻抗最小，相频特性曲线斜率为正； 后者在谐振频率点的阻抗最大，相频特性曲线斜率为负。所以，串联回路在谐振时，通过电流Ｉ00最大； 并联回路在谐振时，两端电压U?00最大。 在实际选频应用时，串联回路适合与信号源和负载串联连接，使有用信号通过回路有效地传送给负载；并联回路适合与信号源和负载并联连接，使有用信号在负载上的电压振幅增大。

　　

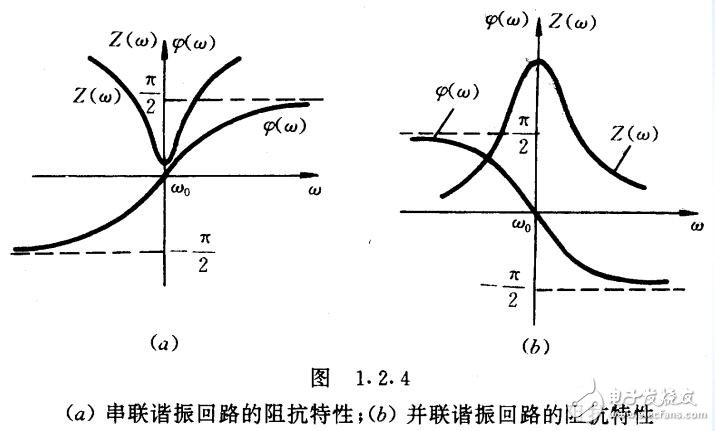
　　串、并联回路的导纳特性曲线正好相反。 前者在谐振频率处的导纳最大，且相频特性曲线斜率为负；后者在谐振频率处的导纳最小，且相频特性曲线斜率为正。读者可自己写出相应的幅频和相频特性表达式， 画出相应的曲线。