正弦交流电的周期与频率详解以及正弦交流电电阻与电容和电感的关系

　　
        我们知道，所谓交流电就是大小和方向都随着时间不断交变的电流。

　　如下右图所示为一正弦交流电的波形图，由图可以得知：交流电跟别的周期性过程一样，是用周期或频率来表示其变化的快慢。正弦交流电由零值增加到正最大值，然后又逐渐减少至零，然后改变方向又由零值逐渐增加到反方向（波形先是向上，然后是向下，所以是反方向）的最大值，最后减少到零。

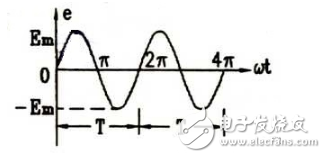
　　正弦交流电这样循环变化一周所需的时间叫做周期，用字母“T”表示。单位是秒（字母“S”表示），常用的还有毫秒（ms）、微妙（μs）、纳秒（ns）。

　　由周期定义可知，周期越大，表面变化一周所需时间越长，即变化越慢，反之周期越小，表面交变电变化一周所需时间越短，即变化越快。

　　交流电在1秒钟内完成周期性变化的次数，叫做交流电的频率，用“f”表示，单位是赫兹，简称赫，用“Hz”表示。频率的常用单位还有千赫（KHz）、兆赫（MHz）

　　周期和频率都是描述交流电变化快慢的物理量，两者的关系为：

　　

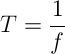
　　除了周期和频率描述交流电的变化快慢外，还可以用电角度（角频率）来描述。角频率用“ω”表示，单位为弧度/秒

　　因为电动势交变一周期，电角度就改变2π弧度，而所需时间为T，所以电角速度（角频率）与频率的关系为：

　　

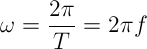
　　由上式可知，周期、频率和角频率三者之间是相互联系的，如果知道其中一个，便可求得另外两个。例如我国电流系统中，交流电的频率是50Hz，则周期T=1/f=0.02s，角频率ω=2πf=314弧度/秒。美国、日本、西欧国家频率是60Hz。

正弦交流电的电容原件

　　线性非时变电容元件C两端加上交流电压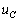时，电容中就将有电流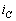流过。若取电容元件支路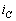的参考方向与电压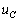的参考方向一致，如图1所示，则有：

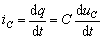　　 （1）

　　当所施加的电压为正弦交流电压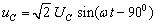时，电容电流为

　　

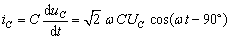
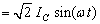　　 （2）

　　电容元件上的电压与电流的变化波形见图1。

　　

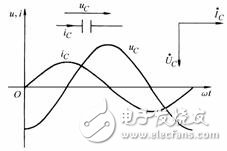
　　图 1

　　由上分析可得，电容上电压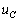与电流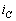为同频率的正弦量，电流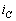在相位上超前电压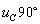。从波形图上可看出，当电容电压过零值时，电压的变化率最大，此时流过电容的电流幅值达到最大振幅值。而当电容电压达到最大幅值时，其电压变化率为零，此时通过电容的电流值也为零。类似于电感元件的情况，电容元件的电流与电压在某些时刻方向一致，而在另一些时刻方向则相反。

　　由式（2）可见，电容元件中电流有效值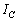与电压有效值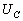之间的关系为

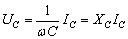　　 （3）

　　式中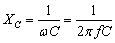，，称为电容的电抗，简称为容抗。当电容C的单位为法拉（F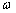），的单位为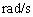时，容抗的单位为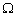，与电阻的量纲相同。

　　正弦交流电的电感

　　线性非时变电感元件是电路中一种重要和基本的元件，在实际电路中经常遇到由导线绕制而成的电感线圈。当电流通过自感为L的线性电感元件时，若取电感元件两端电压与电流的参考方向一致，如图1所示，则由楞次定律知，电流与电压之间的关系式为

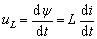　　 （1）

　　式中，L为电感值，单位为亨利（H）。

　　

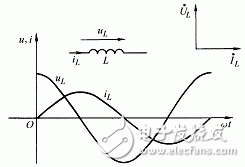
　　图 1

　　当通过电感的电流为正弦交流电流时，即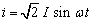，代入上式可得电感元件两端的电压为

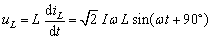
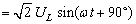　　 （2）

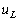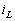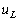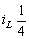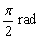　　由上式可见，电感端电压是与同频率的正弦量，电压的相位超前电流周期，即或。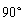

　　从式（2）可得，电感电流的有效值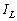与电感端电压的有效值之间有关系式

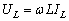　　 （3）

　　式中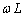，叫做电感线圈的自感电抗，简称感抗，它和电阻具有相同的量纲。当电感L的单位取H，角频率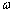的单位取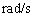时，感抗的单位为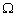。感抗一般用字母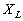表示，即

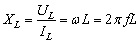　　 （4）

　　例1：一个电阻可忽略的线圈，其电感数值为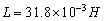，设流过电流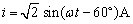，频率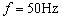，问线圈电压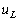为多少？若电流频率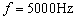，重求线圈端电压。

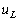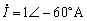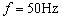　　解：设电流相量，当频率时，感抗

　　

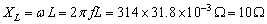
　　由式5可得电压向量：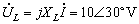

　　则有。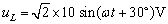

　　当频率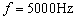时，感抗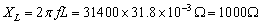，电压向量

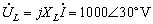　　，电压瞬时式。

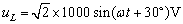　　正弦交流电的电阻元件

　　电阻元件两端的电压与通过它的电流之间关系受欧姆定律约束。当正弦电流流过电阻R时，如图1所示，选定电压与电流的参考方向一致，则根据欧姆定律有：

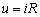　　 （1）

　　若选电流i为参考正弦量，则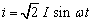，代入上式有：

　　

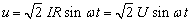
　　电流与电压的波形示于图3-4-1中。由上可见，当流过

　　

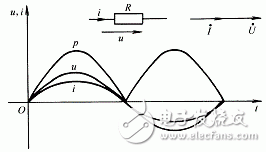
　　图1

　　电阻的电流为正弦函数时，电阻上的电压是与电流同频率的正弦量。电流与电压同相位，它们的有效值也服从欧姆定律，即：

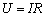　　 （2）

　　如果用相量形式来表示，则有

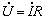　　 （3）

　　上式是复数形式的欧姆定律表达式。该式同时表述了电阻元件上正弦电压与电流之间的相位关系和有效值关系。根据式（3），可画出电压、电流的相量图，如图1所示。