

FIR,IIR滤波器分别是什么?它们又有什么区别?
滤波器电路
描述
什么是FIR滤波器?
FIR(Finite Impulse Response)滤波器:有限长单位冲激响应滤波器,又称为非递归型滤波器,是数字信号处理系统中最基本的元件,它可以在保证任意幅频特性的同时具有严格的线性相频特性,同时其单位抽样响应是有限长的,因而滤波器是稳定的系统。因此,FIR滤波器在通信、图像处理、模式识别等领域都有着广泛的应用。
FIR 滤波器的工作原理是什么?
在进入FIR滤波器前,首先要将信号通过A/D器件进行模数转换,把模拟信号转化为数字信号;为了使信号处理能够不发生失真,信号的采样速度必须满足奈奎斯特定理,一般取信号频率上限的4-5倍做为采样频率;一般可用速度较高的逐次逼进式A/D转换器,不论采用乘累加方法还是分布式算法设计FIR滤波器,滤波器输出的数据都是一串序列,要使它能直观地反应出来,还需经过数模转换,因此由FPGA构成的FIR滤波器的输出须外接D/A模块。FPGA有着规整的内部逻辑阵列和丰富的连线资源,特别适合于数字信号处理任务,相对于串行运算为主导的通用DSP芯片来说,其并行性和可扩展性更好,利用FPGA乘累加的快速算法,可以设计出高速的FIR数字滤波器。
什么是IIR滤波器?
IIR滤波器又叫IIR数字滤波器,“递归滤波器”。递归滤波器,也就是IIR数字滤波器,顾名思义,具有反馈。
IIR滤波器的工作原理及特点是什么?
1.1、封闭函数IIR数字滤波器的系统函数可以写成封闭函数的形式。
1.2、IIR数字滤波器采用递归型结构IIR数字滤波器采用递归型结构,即结构上带有反馈环路。IIR滤波器运算结构通常由延时、乘以系数和相加等基本运算组成,可以组合成直接型、正准型、级联型、并联型四种结构形式,都具有反馈回路。由于运算中的舍入处理,使误差不断累积,有时会产生微弱的寄生振荡。
1.3、借助成熟的模拟滤波器的成果IIR数字滤波器在设计上可以借助成熟的模拟滤波器的成果,如巴特沃斯、契比雪夫和椭圆滤波器等,有现成的设计数据或图表可查,其设计工作量比较小,对计算工具的要求不高。在设计一个IIR数字滤波器时,我们根据指标先写出模拟滤波器的公式,然后通过一定的变换,将模拟滤波器的公式转换成数字滤波器的公式。
1.4、需加相位校准网络IIR数字滤波器的相位特性不好控制,对相位要求较高时,需加相位校准网络。
详细剖析IFR滤波器和LLR滤波器有何本质上的区别?
数字滤波器广泛应用于硬件电路设计,在离散系统中尤为常见,一般可以分为FIR滤波器和IIR滤波器,那么他们有什么区别和联系呢。
FIR滤波器
定义:
FIR滤波器是有限长单位冲激响应滤波器,又称为非递归型滤波器,是数字信号处理系统中最基本的元件,它可以在保证任意幅频特性的同时具有严格的线性相频特性,同时其单位抽样响应是有限长的,因而滤波器是稳定的系统。
特点:
lFIR滤波器的最主要的特点是没有反馈回路,稳定性强,故不存在不稳定的问题;
lFIR具有严格的线性相位,幅度特性随意设置的同时,保证精确的线性相位;
lFIR设计方式是线性的,硬件容易实现;
lFIR相对IIR滤波器而言,相同性能指标时,阶次较高,对CPU的性能要去较高。
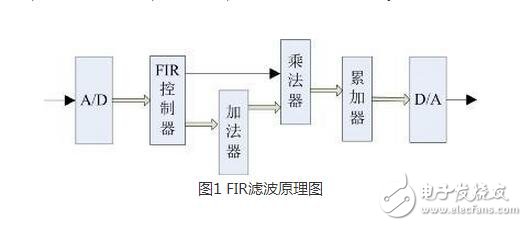
IIR滤波器
定义:
IIR滤波器是无限脉冲响应滤波器,又称递归型滤波器,即结构上带有反馈环路。
特点:
lIIR数字滤波器的系统函数可以写成封闭函数的形式,具有反馈回路;
lIIR数字滤波器的相位非线性,相位特性不好控制,随截止频率变化而变化,对相位要求较高时,需加相位校准网络;
lIIR滤波器有历史的输出参与反馈,同FIR相比在相同阶数时取得更好的滤波效果;
lIIR数字滤波器采用递归型结构,由于运算中的舍入处理,使误差不断累积,有时会产生微弱的寄生振荡。
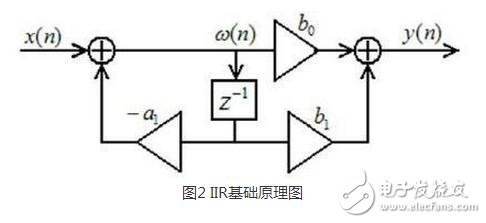
区别
l稳定性:由于FIR滤波器没有反馈回路,稳定性要强于IIR;
l相位特性:FIR 为线性相位延迟,IIR 为非线性相位延迟。
如下图所示为10Hz的方波信号,采样率为1KHz
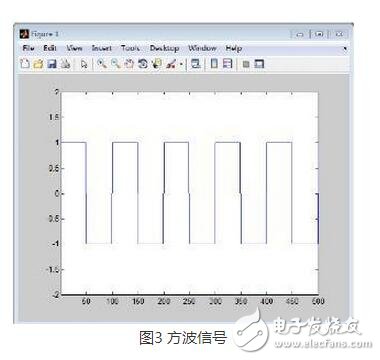
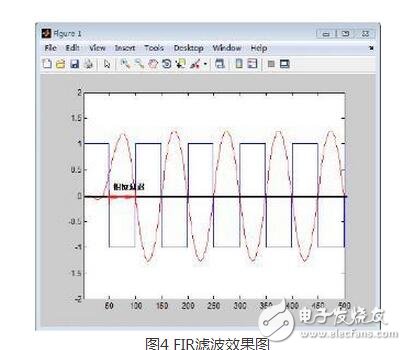
FIR滤波器后,滤波后效果图下图所示
IIR滤波器后,滤波后效果图下图所示
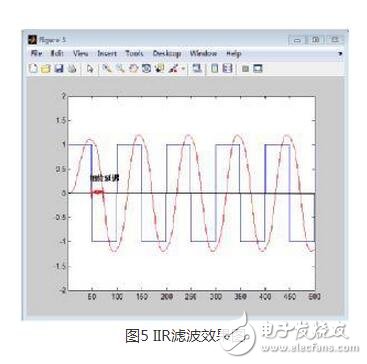
通过对比不难发现,IIR滤波器存在非线性相位延迟,校正时需要双向滤波进行校正,复杂不易控制;FIR滤波器为线性延迟,可通过左右平移的方式直接校正,误差小。
l信号处理速度:FIR的滤波输出取决于当前输入数据和历史输入数据,IIR的滤波输出取决于当前输入数据、历史输入数据和历史输出数据。以基于FPGA硬件的数字滤波器为例,FIR在处理信号时不需等待前一个信号的滤波输出,只需要考虑输入数据便可实时滤波;IIR需要等待上一个信号的滤波输出,存在一定的时间延迟,所以处理速度上没有FIR快。
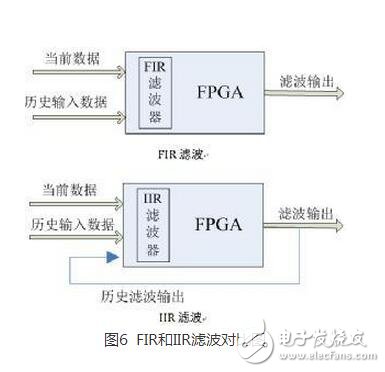
从上面的简单比较可以看到IIR与FIR滤波器各有所长,所以在实际应用时应该从多方面考虑来加以选择。从使用要求上来看,在对相位要求不敏感的场合,如语言通信等,选用IIR较为合适,这样可以充分发挥其经济高效的特点;对于图像信号处理,数据传输等以波形携带信息的系统,则对线性相位要求较高,采用FIR滤波器较好。当然,在实际应用中可能还要考虑更多方面的因素。
-
iir滤波器和fir滤波器的优势和特点2024-07-19 3944
-
FIR滤波器和IIR滤波器的区别与联系有哪些2024-01-29 4296
-
IIR滤波器和FIR滤波器的区别2023-06-03 20425
-
简谈FIR滤波器和IIR滤波器的区别2023-05-29 944
-
FIR滤波器和IIR滤波器的区别与联系2022-12-30 5059
-
FIR滤波器定义及特点2022-08-29 15576
-
IIR滤波器和FIR滤波器详细对比2020-10-30 1944
-
FIR滤波器与IIR滤波器到底有什么区别2020-08-09 33652
-
FIR滤波器和IIR滤波器有什么区别2019-06-27 2184
-
IIR与FIR滤波器的比较和区别2017-11-12 49995
-
详解FIR滤波器和IIR滤波器区别2017-05-04 6454
-
详解FIR滤波器和IIR滤波器的区别2017-05-03 2753
-
FIR滤波器与IIR滤波器的区别与特点2016-08-08 7415
全部0条评论

快来发表一下你的评论吧 !

