

解析微分电路和积分电路的区别
电子常识
描述
一、矩形脉冲信号
在数字电路中,经常会碰到如图4-16所示的波形,此波形称为矩形脉冲信号。其中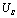 为脉冲幅度,
为脉冲幅度,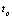 为脉冲宽度,
为脉冲宽度, 为脉冲周期。
为脉冲周期。
当矩形脉冲作为RC串联电路的激励源时,选取不同的时间常数及输出端,就可得到我们所希望的某种输出波形,以及激励与响应的特定关系。
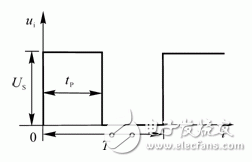
图4-16 脉冲信号
二、微分电路
在图4-17所示电路中,激励源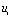 为一矩形脉冲信号,响应是从电阻两端取出的电压,即
为一矩形脉冲信号,响应是从电阻两端取出的电压,即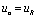 ,电路时间常数小于脉冲信号的脉宽,通常取
,电路时间常数小于脉冲信号的脉宽,通常取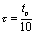 。
。
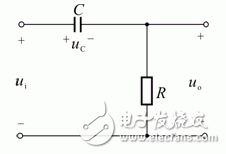
图4-17 微分电路图
因为t《0时,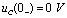 ,而在t = 0 时,
,而在t = 0 时,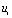 突变到
突变到 ,且在0《 t 《 t1期间有:
,且在0《 t 《 t1期间有: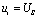 ,相当于在RC串联电路上接了一个恒压源,这实际上就是RC串联电路的零状态响应:
,相当于在RC串联电路上接了一个恒压源,这实际上就是RC串联电路的零状态响应: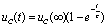 。由于
。由于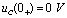 ,则由图4-17电路可知
,则由图4-17电路可知 。所以
。所以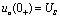 ,即:输出电压产生了突变,从0 V突跳到
,即:输出电压产生了突变,从0 V突跳到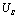 。
。
因为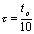 ,所以电容充电极快。当
,所以电容充电极快。当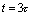 时,有
时,有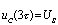 ,则
,则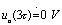 。故在
。故在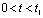 期间内,电阻两端就输出一个正的尖脉冲信号,如图4-18所示。
期间内,电阻两端就输出一个正的尖脉冲信号,如图4-18所示。
在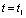 时刻,
时刻,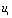 又突变到0 V,且在
又突变到0 V,且在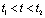 期间有:
期间有: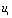 = 0 V,相当于将RC串联电路短接,这实际上就是RC串联电路的零输入响应状态:
= 0 V,相当于将RC串联电路短接,这实际上就是RC串联电路的零输入响应状态: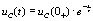 。
。
由于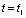 时,
时,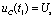 ,故
,故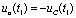 。
。
因为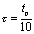 ,所以电容的放电过程极快。当
,所以电容的放电过程极快。当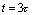 时,有
时,有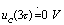 ,使
,使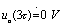 ,故在
,故在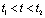 期间,电阻两端就输出一个负的尖脉冲信号,如图4-18所示。
期间,电阻两端就输出一个负的尖脉冲信号,如图4-18所示。
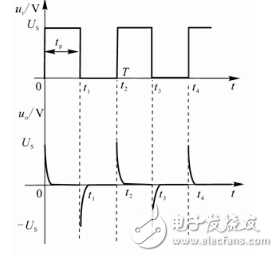
图4-18 微分电路的ui与uO波形
由于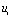 为一周期性的矩形脉冲波信号,则
为一周期性的矩形脉冲波信号,则 也就为同一周期正负尖脉冲波信号,如图4-18所示。
也就为同一周期正负尖脉冲波信号,如图4-18所示。
尖脉冲信号的用途十分广泛,在数字电路中常用作触发器的触发信号;在变流技术中常用作可控硅的触发信号。
这种输出的尖脉冲波反映了输入矩形脉冲微分的结果,故称这种电路为微分电路。
微分电路应满足三个条件:① 激励必须为一周期性的矩形脉冲;② 响应必须是从电阻两端取出的电压;③ 电路时间常数远小于脉冲宽度,即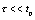 。
。
三、积分电路
在图4-19所示电路中,激励源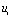 为一矩形脉冲信号,响应是从电容两端取出的电压,即
为一矩形脉冲信号,响应是从电容两端取出的电压,即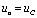 ,且电路时间常数大于脉冲信号的脉宽,通常取
,且电路时间常数大于脉冲信号的脉宽,通常取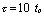 。
。
因为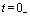 时,
时,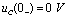 ,在t =0时刻
,在t =0时刻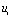 突然从0 V上升到
突然从0 V上升到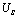 时,仍有
时,仍有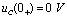 ,
,
故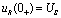 。在
。在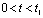 期间内,
期间内, ,此时为RC串联状态的零状态响应,即
,此时为RC串联状态的零状态响应,即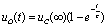 。
。
由于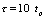 ,所以电容充电极慢。当
,所以电容充电极慢。当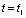 时,
时, 。电容尚未充电至稳态时,输入信号已经发生了突变,从
。电容尚未充电至稳态时,输入信号已经发生了突变,从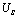 突然下降至0 V。则在
突然下降至0 V。则在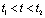 期间内,
期间内,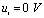 ,此时为RC串联电路的零输入响应状态,即
,此时为RC串联电路的零输入响应状态,即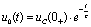 。
。
由于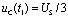 ,所以电容从
,所以电容从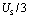 处开始放电。因为
处开始放电。因为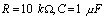 ,放电进行得极慢,当电容电压还未衰减到
,放电进行得极慢,当电容电压还未衰减到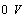 时,
时,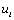 又发生了突变并周而复始地进行。这样,在输出端就得到一个锯齿波信号,如图4-20所示。
又发生了突变并周而复始地进行。这样,在输出端就得到一个锯齿波信号,如图4-20所示。
锯齿波信号在示波器、显示器等电子设备中作扫描电压。
由图4-20波形可知:若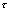 越大,充、放进行得越缓慢,锯齿波信号的线性就越好。
越大,充、放进行得越缓慢,锯齿波信号的线性就越好。
从图4-20波形还可看出,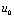 是对
是对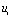 积分的结果,故称这种电路为积分电路。
积分的结果,故称这种电路为积分电路。
RC积分电路应满足三个条件:① 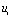 为一周期性的矩形波;② 输出电压是从电容两端取出;③电路时间常数远大于脉冲宽度,即
为一周期性的矩形波;② 输出电压是从电容两端取出;③电路时间常数远大于脉冲宽度,即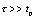 。
。
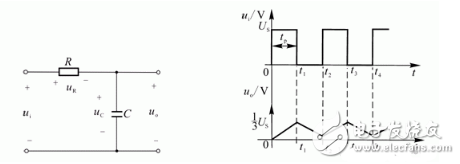
图4-19 积分电路图 图4-20 积分电路的ui与uo波形
【例4-6】 在图4-21(a)所示电路中,输入信号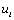 的波形如图4-21(b)所示。试画出下列两种参数时的输出电压波形。并说明电路的作用。
的波形如图4-21(b)所示。试画出下列两种参数时的输出电压波形。并说明电路的作用。
① 当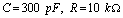 时;② 当
时;② 当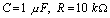 时。
时。
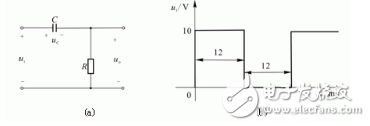
图4-21 电路图图
解:① 因为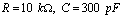 ,所以
,所以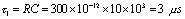 ,
,
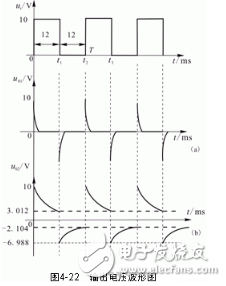
而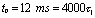 ,显然,此时电路是一个微分电路,其输出电压波形如图4-22(a)所示。
,显然,此时电路是一个微分电路,其输出电压波形如图4-22(a)所示。
② 因为为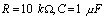 .
.
而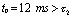 ,但
,但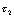 很接近于
很接近于 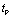 。所以电容充电较慢,即
。所以电容充电较慢,即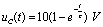 。
。
故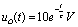 ,所以当
,所以当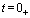 时,
时,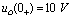 ,
,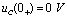 ;
;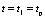 时,
时,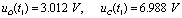 。
。
此时,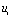 已从10 V突跳到0 V,则电容要经电阻放电,即
已从10 V突跳到0 V,则电容要经电阻放电,即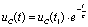 。
。
所以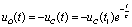 。
。
则当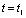 时,
时,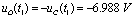 ;
;
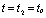 时,
时,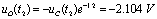 。
。
输出电压波形如图4-22(b)所示。。
由图4-22可知:当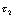 越大时,
越大时,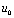 波形就越接近于
波形就越接近于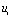 波形。所以,此时的电路就称为耦合电路。
波形。所以,此时的电路就称为耦合电路。
-
运算放大器应用电路之微分电路2022-11-04 7260
-
RC微分电路与RC积分电路有什么不同2011-11-07 13049
-
微分与积分电路2006-04-16 3443
-
积分与微分电路实验2009-05-15 23937
-
基本微分电路2010-04-23 4679
-
微分和积分电路的异同2011-08-03 27566
-
微分电路基本概念和电路图解析2017-05-12 21638
-
积分电路和微分电路的形成条件与基本特点2017-11-01 115611
-
微分电路的应用2019-06-20 9055
-
滤波器电路分析————积分电路、微分电路资料下载2021-04-02 1214
-
Multisim仿真之微分积分电路2022-04-08 2315
-
积分与微分电路原理详解2022-11-09 3184
-
【凡亿疯狂星期五】微分电路和积分电路构成及特点介绍2023-08-10 1447
-
为什么电路中有积分电路和微分电路,Python中无法对某个函数直接求导?2023-10-26 1146
-
积分电路和微分电路的区别2024-01-16 5311
全部0条评论

快来发表一下你的评论吧 !

