

加法器是什么?加法器的原理,类型,设计详解
电子常识
描述
加法器的简介
加法器是为了实现加法的。即是产生数的和的装置。加数和被加数为输入,和数与进位为输出的装置为半加器。若加数、被加数与低位的进位数为输入,而和数与进位为输出则为全加器。常用作计算机算术逻辑部件,执行逻辑操作、移位与指令调用。对于1位的二进制加法,相关的有五个的量:
1,被加数A,
2,被加数B,
3,前一位的进位CIN,
4,此位二数相加的和S,
5,此位二数相加产生的进位COUT。前三个量为输入量,后两个量为输出量,五个量均为1位。对于32位的二进制加法,相关的也有五个量:
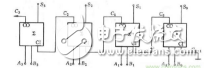
加法器的原理
1,被加数A(32位),
2,被加数B(32位),
3,前一位的进位CIN(1位),
4,此位二数相加的和S(32位),
5,此位二数相加产生的进位COUT(1位)。
要实现32位的二进制加法,一种自然的想法就是将1位的二进制加法重复32次(即逐位进位加法器)。这样做无疑是可行且易行的,但由于每一位的CIN都是由前一位的COUT提供的,所以第2位必须在第1位计算出结果后,才能开始计算;第3位必须在第2位计算出结果后,才能开始计算,等等。而最后的第32位必须在前31位全部计算出结果后,才能开始计算。这样的方法,使得实现32位的二进制加法所需的时间是实现1位的二进制加法的时间的32倍。
可以看出,上法是将32位的加法1位1位串行进行的,要缩短进行的时间,就应设法使上叙进行过程并行化。逐位进位加法器,在每一位的计算时,都在等待前一位的进位。那么不妨预先考虑进位输入的所有可能,对于二进制加法来说,就是0与1两种可能,并提前计算出若干位针对这两种可能性的结果。等到前一位的进位来到时,可以通过一个双路开关选出输出结果。这就是进位选择加法器的思想。提前计算多少位的数据为宜?同为32位的情况:线形进位选择加法器,方法是分N级,每级计算32/N位;平方根进位选择加法器,考虑到使两个路径
1,提前计算出若干位针对这两种可能性的结果的路径,
2,上一位的进位通过前面的结构的路径的延时达到相等或是近似。
方法,或是2345666即第一级相加2位,第二级3位,第三级4位,第四级5位,第五级6位,第六级6位,第七级6位;或是345677即第一级相加3位,第二级4位,第三级5位,第四级6位,第五级7位,第六级7位。进一步分析加法进行的机制,可以使加法器的结构进一步并行化。令G=AB,P=A⊕B,则COUT(G,P)=G+PCIN,S(G,P)=P⊕CIN。由此,A,B,CIN,S,COUT五者的关系,变为了G,P,CIN,S,COUT五者的关系。再定义点运算(*),(G,P)*(G’,P’)=(G+PG’,PP’),可以分解(G3:2,P3:2)=(G3,P3)(G2,P2)。
点运算服从结合律,但不符合交换律。点运算只与G,P有关而与CIN无关,也就是可以通过只对前面若干位G,P进行点运算计算,就能得到第N位的GN:M,PN:M值,当取M为0时,获得的GN:0,PN:0即可与初使的CIN一起代入COUT(G,P)=G+PCIN,S(G,P)=P⊕CIN,得到此位的COUT,S;而每一位的G,P值又只与该位的A,B值即输入值有关,所以在开始进行运算后,就能并行的得到每一位的G,P值。以上分析产生了超前进位加法器的思想:三步运算,1,由输入的A,B算出每一位的G,P;2,由各位的G,P算出每一位的GN:0,PN:0;3,由每一位的GN:0,PN:0与CIN算出每一位的COUT,S。其中第1,3步显然是可以并行处理的,计算的主要复杂度集中在了第2步。第2步的并行化,也就是实现GN:0,PN:0的点运算分解的并行化。
加法器的优化设计
逻辑改造后,电路也应该相应地进行优化设计,因为如果用普通的门电路来实现式(12)~(15)的逻辑,晶体管数目(面积)会增加。另外,在电路级也可以采用减少节点翻转和寄生电容的方法来降低功耗。式(12)~(15)中多处要用到同或门,设计中,我们用基于旁路的静态逻辑实现产生gs的同或门,如图2。旁路逻辑通过由附加管形成的旁路,可以把“串并交错”的电路结构简化为单一的串或者并的形式。它的电路和版图都有很好的规整性,并且可以减小寄生电容。是两种同或门N块版图不同部分的比较,(b)是基于旁路逻辑实现的,与(a)相比,少了一条金属连线和两个金属接触,使版图变得十分规整,扩散区不会被隔断。
在拓扑上,两条分支用公共的漏区,达到最少的接触孔和金属互连,比“串并”和“并串”的晶体管配置方式规整,且寄生电容小。加法器电路上的延迟值旁路逻辑不能实现传输门,因而不能用传输门实现同或和异或,但是容易证明,三态门在速度和功耗方面都比传输门优越。
参照传输门的结合方式,我们用两个三态反相器和一个反相器实现了同或门。实现了式(13)括号内的两个同或逻辑,平均只需要1级门延时,而用普通门实现的“与非或与非”形式的同或门需要2级或3级门延时。由上面的同或门设计得到启发,根据形如式(13)的逻辑,设计了一个10管单元utiandor2。
该单元电路实现s=c0CK+0CKN,只要把式(12)~(15)中的括号部分从CK和CKN输入,输出就相应得到了s0~s3。仅当CKN=时,电路(a)两边均是三态反相器,构成图5(b)的同或门,两个反相器交替导通,s=c0⊙CK;当CKN=CK(发生几率比较大),左边P管和右边N管,或者左边N管和右边P管交替导通,输出s=CK,从而屏蔽了c0的变化。考察第一组4位CLA中的进位产生逻辑最复杂的s3,参考式(15),当g2,g1,g0均为0,p2,p1,p0均为1时,s3=gs3⊙c0,显然这是一种特殊情况,即低位各位都不产生进位,但可以传递进位时,直接把c0传至高位与gs同或即可产生和。c0在各位和生成逻辑的最后一级才加入,可以消除过早加入带来的不必要的翻转。左右两块交替导通,只存在下拉或上拉延时,有类似动态电路延迟小的优点。仅用了10个晶体管,比常规门实现的积之和节省8个。
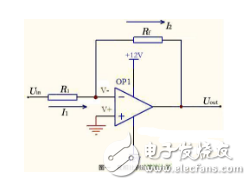
加法器的类型
全加器引入了进制值的输入,以计算较大的数。为区分全加器的两个进制线,在输入端的记作Ci或Cin,在输出端的则记作Co或Cout。半加器简写为H.A.,全加器简写为F.A.。半加器:半加器的电路图半加器有两个二进制的输入,其将输入的值相加,并输出结果到和(Sum)和进制(Carry)。半加器虽能产生进制值,但半加器本身并不能处理进制值。全加器:全加器三个二进制的输入,其中一个是进制值的输入,所以全加器可以处理进制值。全加器可以用两个半加器组合而成。
- 相关推荐
- 加法器
-
FPU加法器的设计与实现2012-07-06 1026
-
加法器2016-10-20 0
-
什么类型的加法器将被合成到?2020-03-19 0
-
什么是加法器?加法器的原理是什么 ?2021-03-11 0
-
加法器,加法器是什么意思2010-03-08 5580
-
十进制加法器,十进制加法器工作原理是什么?2010-04-13 13715
-
8位加法器和减法器设计实习报告2013-09-04 2540
-
同相加法器电路原理与同相加法器计算2016-09-13 57697
-
加法器设计代码参考2021-05-31 956
-
运算放大器的同相加法器和反相加法器2022-08-05 31699
-
加法器的原理及采用加法器的原因2023-06-09 5227
-
镜像加法器的电路结构及仿真设计2023-07-07 2970
-
同相加法器和反相加法器的区别是什么2024-05-23 2765
-
加法器的原理是什么 加法器有什么作用2024-05-23 3350
-
串行加法器和并行加法器的区别?2024-05-23 2808
全部0条评论

快来发表一下你的评论吧 !

