

基于CW32的仪表精度测量实现(一):相关滤波原理
描述
一、滤波的概念
滤波是指通过某种方法将信号中的某些频率成分增强或抑制,达到去除噪声、改善信号质量、分离信号等目的的过程。滤波器是实现滤波功能的关键组件,它可以改变信号的频谱特性,对不同频率区域的信号进行处理。
二、常见的滤波算法
1.小波变换滤波
原理:小波变换通过将信号分解成不同尺度的子信号,可以提取出信号中的局部特征。在滤波中,小波变换可以用来去除信号中的噪声或者对信号进行平滑处理。
下面是该算法的波形图:
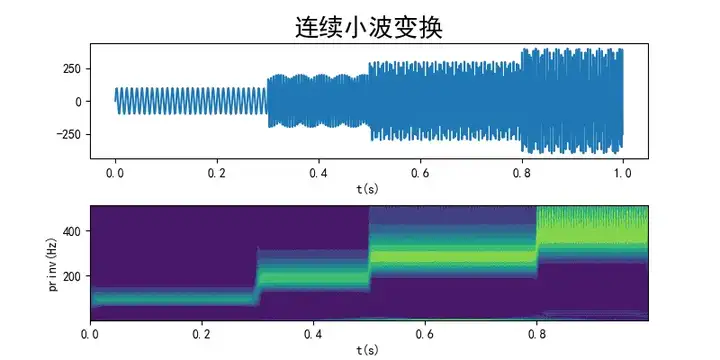
使用场景:
(1)图像去噪:小波变换可以有效地去除图像中的噪声,尤其是在多尺度分解中,可以针对不同频率的噪声进行过滤。
(2)特征提取:小波变换能够揭示图像或信号中的局部特征,因此在特征提取方面非常有用,比如在图像识别和分类中。
(3)边缘检测:小波变换在边缘检测方面表现出色,因为它能够捕捉到图像中的尖锐变化。
(4)信号去噪:在信号处理中,小波变换可以用于去除信号中的噪声,尤其是在非平稳信号中。
2.移动平均滤波
原理:首先确定一个包含一定数量样本点的窗口,这个窗口在信号上滑动。在每一个位置,计算窗口内所有样本点的平均值。将计算得到的平均值作为滤波后的输出。将窗口沿信号滑动一定步长,重复上述步骤。
我们有一个离散时间信号 x[n],并且我们使用长度为 M 的窗口进行移动平均滤波,那么滤波后的信号 y[n] 可以通过以下公式计算:则计算公式为:
y[n]=1/M∑k=n−M+1nx[k]
例如:一个包含噪声的信号序列x=[1,4,3,6,6,5,10,9,7,12].
我们可以使用移动平均滤波来平滑信号并减小噪声的影响。假设我们选择一个窗口大小为3,即每次计算三个样本的平均值。
第一个输出样本为:y[0]=(1/3)∗(1+4+3)=2.666
第二个输出样本为:y[1]=(1/3)∗(4+3+6)=4.33
以此类推,我们可以继续计算后续输出样本。
下面是使用这个算法生成的一个波形图
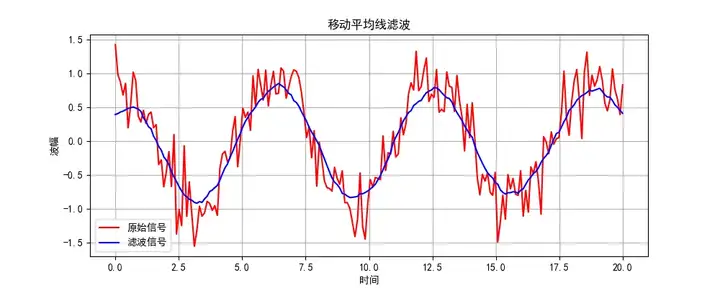
使用场景:
(1)在金融领域等需要对数据进行趋势分析的场景中,移动平均滤波可以平滑价格波动,帮助分析数据的长期趋势,预测未来走势。
(2)在实时数据处理或传感器数据处理中,移动平均滤波可以利用先前时刻的数据进行滤波处理,对新的数据进行平均,有助于消除数据中的噪声或异常值。
(3)移动平均滤波对周期性噪声和高频噪声的滤波效果比较好,可以很好地降低信号或数据中的高频成分,同时保留信号的基本特征。
3.中值滤波
原理:中值滤波会选取数字图像或数字序列中像素点及其周围临近像素点(一共有奇数个像素点)的像素值,将这些像素值排序,然后将位于中间位置的像素值作为当前像素点的像素值,让周围的像素值接近真实值,从而消除孤立的噪声点。例如,针对下图中第4行第3列的像素点,计算它的中值滤波值。
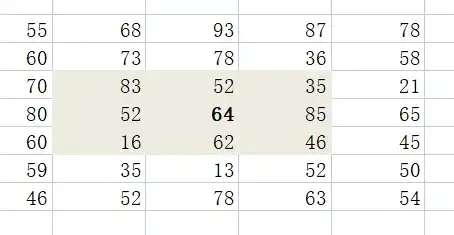
将其邻域设置为3×3大小,对其3×3邻域内像素点的像素值进行排序(升序降序均可),按升序排序后得到序列值为:[16,35,46,52,52,62,64,83,85],在该序列中,处于中心位置(也叫中心点或中值点)的值是“52”,因此用该值替换原来的像素值 64,作为当前点的新像素值,新的像素图如下所示。
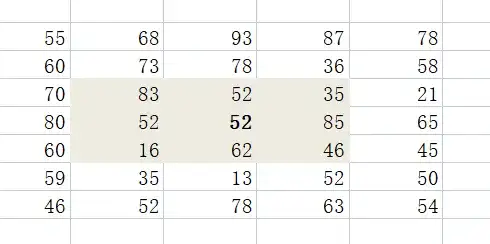
下面是使用这个算法对随机噪声滤波后生成的一个波形图:
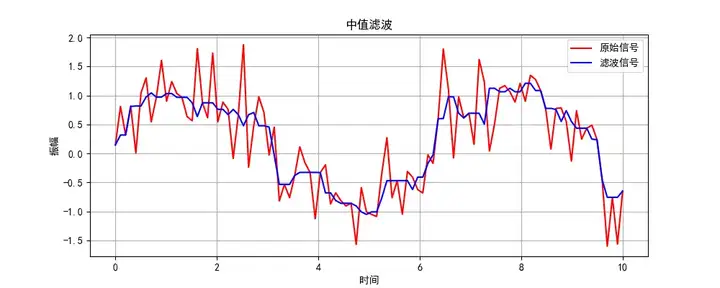
使用场景:
(1)孤立噪声点平滑:中值滤波能有效去除图像或信号中的孤立噪声点,而不会对整体图像或信号的平滑区域造成影响。
(2)椒盐噪声去除:中值滤波对椒盐噪声(salt-and-pepper noise)具有很好的滤除效果,这种噪声表现为图像中随机分布的白色和黑色像素点。
(3)实时视频处理:由于中值滤波算法的计算复杂度相对较低,它可以用于实时视频流的噪声去除。
4.算术平均滤波
原理:算术平均滤波是图像处理中的一个常用技术,主要用于降低图像中的随机噪声。算术平均滤波器的基本思想是用像素点邻域内的平均灰度值来代替该像素点的灰度值。
算术平均滤波的计算公式如下:
f'(x, y) = 1/(mn) * ΣΣf(x+k, y+l)
其中,f'(x, y)是滤波后像素点(x, y)的灰度值,f(x+k, y+l)是原像素点(x, y)领域内的灰度值,ΣΣ表示对领域内所有像素点求和,m和n是滤波窗口的大小。
下面是使用这个算法对随机噪声滤波后生成的一个波形图:
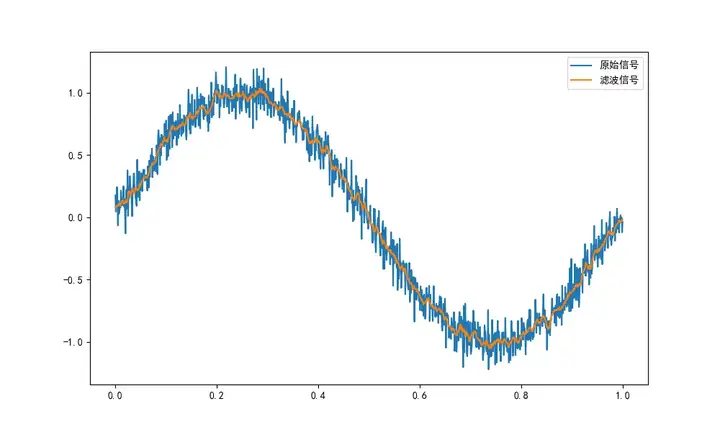
算术平均滤波适用于一些简单的图像或信号处理场景,例如去除较为均匀且较弱的噪声。
5.卡尔曼滤波
原理:
(1)预测步骤(预测状态):通过系统的动态模型,根据已知的系统状态和控制量,预测系统的下一个状态以及状态的协方差。这一步骤得到的是对系统未来状态的预测。
(2)测量更新步骤(更新状态):利用传感器测量数据,根据预测的状态和测量数据的协方差,通过卡尔曼增益计算得到关于系统状态的修正估计。卡尔曼增益会根据预测和测量的不确定性来调整估计值,以平衡两者之间的权重。
下面是使用这个算法对随机噪声滤波后生成的一个波形图:
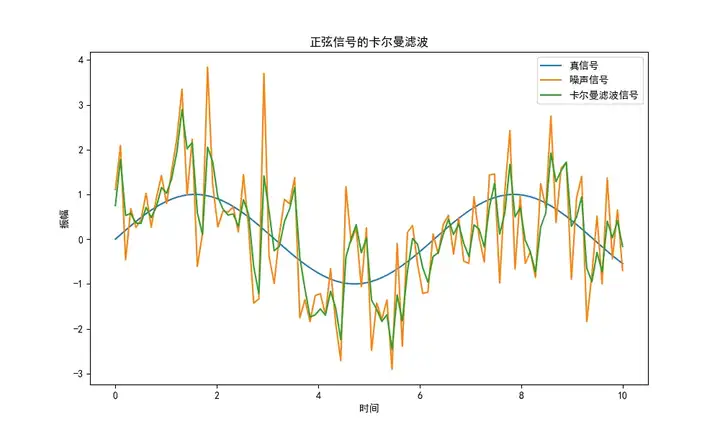
使用场景:卡尔曼滤波广泛应用于估计动态系统的状态,例如航天器导航、飞行器控制、传感器数据融合等领域。它具有高效、准确、稳定等优点,能够处理系统模型不确定性、传感器误差等问题,提高状态估计的精度和鲁棒性。
6.均值滤波
原理:连续采样N个数据,去掉一个最大值和一个最小值然后计算N-2个数据的算术平均值N值的选取
下面是使用这个算法对随机噪声滤波后生成的一个波形图:
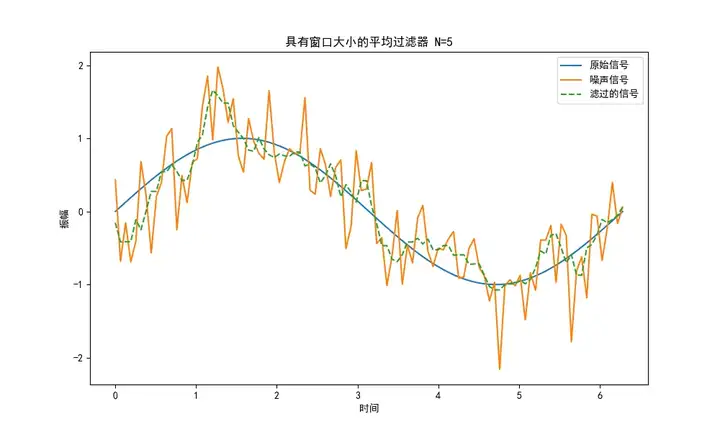
使用场景:
(1)工业自动化:在工业自动化和控制系统中,均值滤波用于从传感器数据中去除噪声,提高系统的稳定性和可靠性。
(2)信号平滑:当信号受到高频干扰或随机噪声时,中值平均滤波法可以将突然的干扰降低,使信号变得更加平滑。
(3)环境监测:在环境监测中,均值滤波可以用于处理大气、水质等监测数据,去除测量误差和随机波动。
(4)数字图像处理:在数字图像处理中,中值平均滤波法常用于去除图像中的噪声,例如在数字摄影中去除低光照条件下的图像噪声。
7.快速傅里叶变换(FFT)滤波
原理:FFT滤波将时域信号通过FFT算法转换到频域,得到信号在频域上的频谱信息。在频域上对信号进行滤波处理,可以采用各种滤波器,如低通滤波器、高通滤波器、带通滤波器等,以抑制或增强特定频率成分。对经过滤波处理的频域信号进行逆FFT,将信号恢复回时域。
我使用python生成了一个频率为50 Hz的正弦波信号,并添加了高斯噪声。然后,使用numpy.fft.fft函数计算信号的FFT,并使用numpy.fft.fftfreq生成对应的频率向量。接下来,设计了一个简单的低通滤波器,只允许截止频率以下的频率成分通过。应用滤波器后,使用numpy.fft.ifft计算逆FFT,得到滤波后的信号。
下面是滤波的效果图:
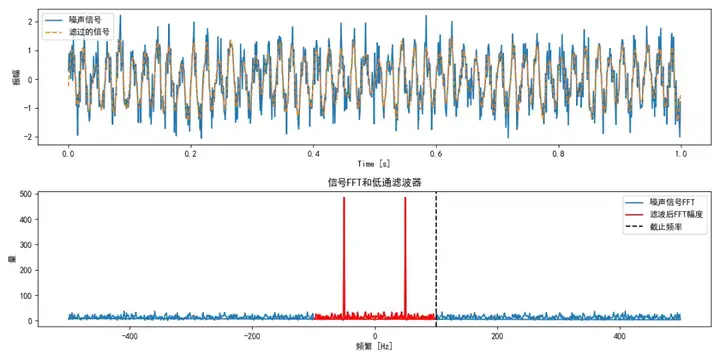
使用场景:
(1)频域滤波:FFT允许将时域信号转换到频域,然后可以轻松地应用各种滤波器,如低通、高通、带通和带阻滤波器。
(2)信号分析:FFT常用于分析信号的频率成分,识别信号中的周期性成分或检测特定频率的信号。
(3)图像处理:在图像处理中,FFT可以用于频域滤波,如锐化、模糊、边缘检测等。
审核编辑 黄宇
-
基于芯源CW32 MCU的LED闪烁示例及代码分析2025-12-04 69
-
CW32量产烧录工具2024-04-25 2609
-
CW32快速开发入门2024-04-24 3335
-
基于CW32的无刷水泵方案2023-11-03 1849
-
基于CW32的RC522刷卡模块的应用2023-11-02 2406
-
基于CW32热敏电阻采集温度应用2023-10-25 1188
-
CW32实时时钟(RTC)介绍2023-10-24 2030
-
CW32 PWM输出功能介绍2023-09-27 1972
-
cw32和stm32的区别2023-08-16 6141
-
【应用笔记】CW32 电容式触摸按键设计指南2023-07-04 1855
-
CW32开发者扶持计划#CW32 #芯片CW32生态社区 2023-05-24
-
【CW32移植Free-RTOS】CW32开发者扶持计划2023-04-18 7194
-
应用笔记-CW32 自举程序中使用的 ISP 协议2022-06-06 834
全部0条评论

快来发表一下你的评论吧 !

