网孔电流法例题_回路电流法例题

　　回路电流法是以一组独立回路电流作为变量列写电路方程求解电路变量的方法。倘若选择基本回路作为独立回路，则回路电流即是各连支电流。以回路电流为变量列写方程求解电路的方法称为回路电流法，简称回路法。回路法对平面和非平面网络均适用。

　　电路网孔电流法和回路电流法例题

　　一、网孔电流法

　　1.网孔电流法的引出

　　问题：支路电流法的规律性不强，当电路的结构相对复杂且支路数较多时，手工求解会很困难。

　　目标：寻找一组相互独立的电路变量，它们具有较少的数目，且能够用它们表征电路中任意的物理量，从而有效减少电路方程数量，有助于求解电路。

　　基本思想：在平面电路中为减少未知量（方程）的个数，可以假想每个网孔中有一个网孔电流。若网孔电流已求得，则各支路电流可用网孔电流的线性组合表示。这样即可求得电路的解。

　　2.网孔电流法：以网孔电流作为电路的独立变量，对每个网孔列KVL方程。（仅适用于平面电路）

　　

　　网孔电流：沿着网孔流动的假想电流。

　　网孔电流法的独立方程数为b-（n- 1）。

　　与支路电流法相比，方程数减少了（n-1）个。

　　

　　假想有两个电流Im1和Im2分别沿此平面电路的两个网孔连续流动：

　　支路1只有电流Im1流过，且Im1绕行方向与I1 相同，即：I1 = Im1；

　　支路2只有电流im2流过，且Im2 绕行方向与I2 相同，即：I2 = Im2；

　　支路3有2个网孔电流同时流过，且Im1 、Im2绕行方向都与I3相同。

　　则： I3 = Im1 +Im2 （自动满足结点a 的KCL方程）

　　则：三个支路电流I1 、 I2、 I3 可分别用两个网孔电流Im1 、 Im2的线性组合表示。

　　

　　自阻Rkk ：网孔k中所有电阻之和。

　　互阻Rkj ：两个网孔k、j的共有电阻。当网孔k、j在其互阻上绕行方向相同时，互阻Rkj取正；反之则取负。

　　上例中，网孔1的自阻： R11 = R1 +R3 ， 网孔2的自阻： R22 = R2+R3 ， 网孔1和网孔2的互阻：R12 = R21 = R3 。

　　对具有L个网孔的平面电路，网孔电流方程的一般形式为：

　　

　　几点说明：

　　（1）两个网孔之间若没有共有支路，或者有共有支路但其电阻为零（例如共有支路间仅有电压源），则互阻为零。

　　（2）如果将所有网孔电流都取为顺（或逆）时针方向，则所有互阻总是负的。

　　（3）在不含受控源的电阻电路中： Rkj = Rjk 。

　　（4）方程右边USkk为网孔k中所有电压源电压的代数和，各电压源的极性与网孔电流绕行方向非关联时取正， 反之则取负。

　　网孔电流方程的KVL形式表示了在一个网孔中各个网孔电流在各个电阻上所产生的电压降等于此网孔中所有电压源的电压代数和（电势升）。

　　网孔电流法的一般步骤：

　　（1）选定电路中各个网孔的绕行方向；

　　（2）对m个网孔，以网孔电流为未知量，列写其KVL方程；

　　（3）求解上述方程，得到m个网孔电流；

　　（4）求各支路电流（用网孔电流表示）；

　　（5）其它分析。

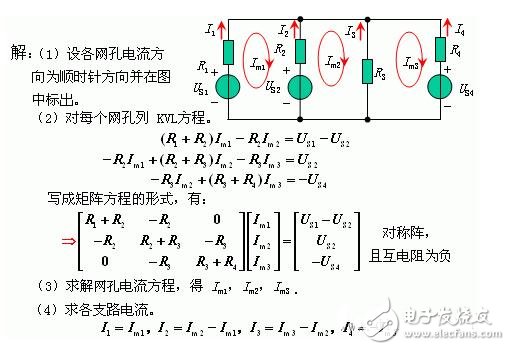
　　例6. 求各支路电流。

　　

　　3.含电流源支路的处理

　　（1）含电流源与电阻并联支路的处理

　　例7.列写如图电路的网孔电流方程。

　　设各网孔电流方向为顺时针方向并在图中标出。

　　KVL：

　　

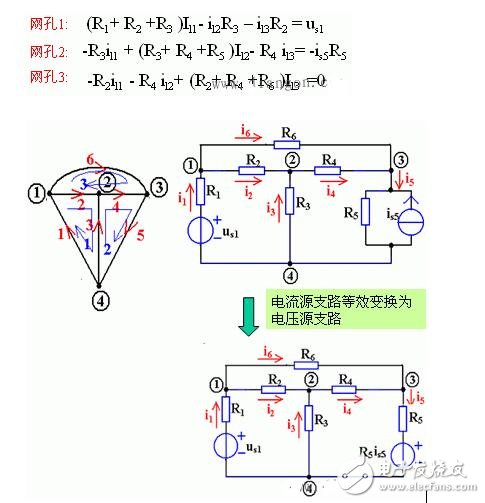
　　（2）含无伴电流源支路的处理

　　例８。列写如图电路的网孔电流方程（含无伴电流源支路）。

　　

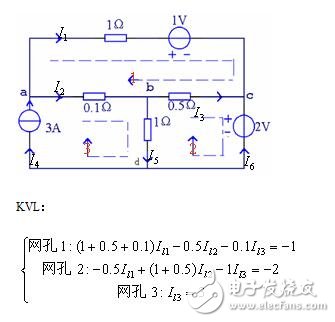
　　例9.列写含有无伴电流源支路的电路的网孔电流方程。

　　

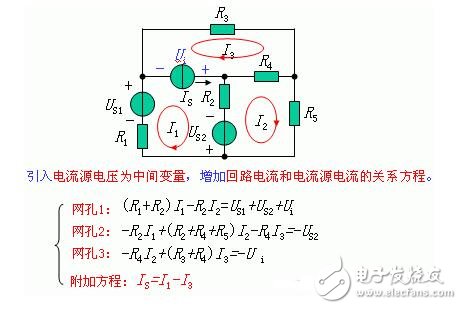
　　引入电流源电压为中间变量，增加回路电流和电流源电流的关系方程。

　　4.含受控源支路的处理

　　例10. 用网孔电流法求下图所示电路的各支路电流。

　　

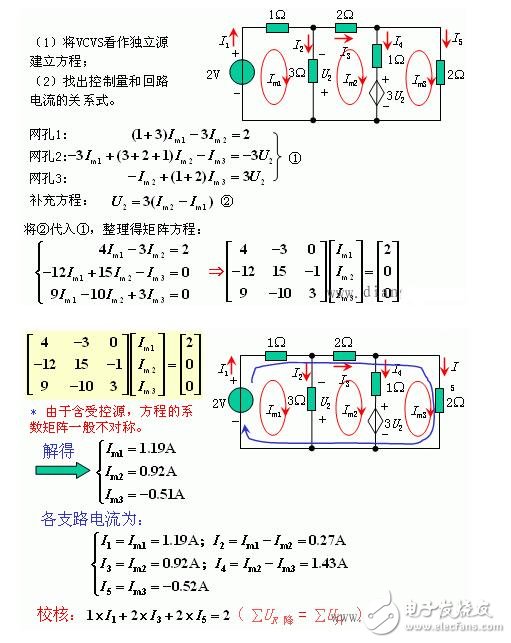
　　二、回路电流法

　　1.回路电流法：以一组独立回路电流作为电路的独立变量，对每个回路列KVL方程分析电路的方法。

　　回路电流：在一个回路中连续流动的假想电流。

　　网孔电流法仅适用于平面电路，回路电流法则无此限制，它适用于平面或非平面电路。因此回路电流法是一种适用性较强并获得广泛应用的分析方法。

　　常选基本回路（单连支回路）作为独立回路，则回路电流即相应的连支电流，树支电流可以用连支电流或回路电流表示。

　　例：在右图电路中，

　　

　　

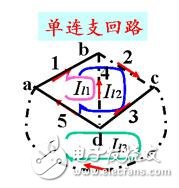
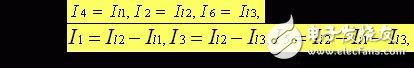
　　（自动满足结点b，c，a 的KCL方程）

　　全部支路电流可以通过回路电流表示。

　　在回路电流法中，只需按KVL列方程，不必再列KCL方程。

　　回路电流方程的一般形式：（独立回路数l = b - n + 1）

　　

　　uSkk — 回路k中所有电压源电压的代数和。

　　uSkk－当回路中各个电压源电压的方向与该回路绕向关联时，取负号；非关联时，取正号。

　　回路电流法的一般步骤：

　　（1）选定l=b-（n-1）个独立回路，标明回路电流及方向；

　　（2）对l个独立回路，以回路电流为未知量，列写其KVL方程；

　　（3）求解上述方程，得到l个回路电流；

　　（4）求各支路电流（用回路电流表示）；

　　（5）其它分析。

　　例11.

　　

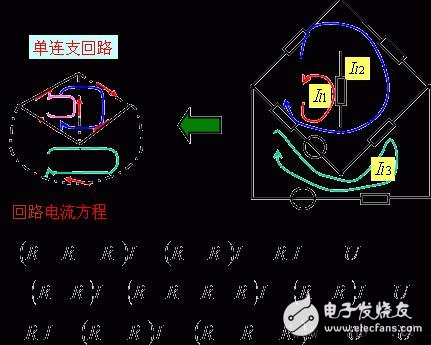
　　2.电路中具有电流源情况的分析

　　例12.列写含有无伴电流源支路的电路的回路电流方程。

　　选取独立回路时，使无伴电流源支路仅仅属于一个回路，该回路电流已知，即 IS ，所以不用再对其列KVL方程。

　　

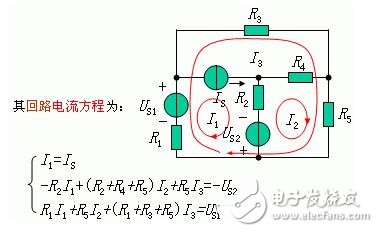
　　3.电路中具有受控源情况的分析

　　例13.列写下图所示含受控源电路的回路电流方程。

　　

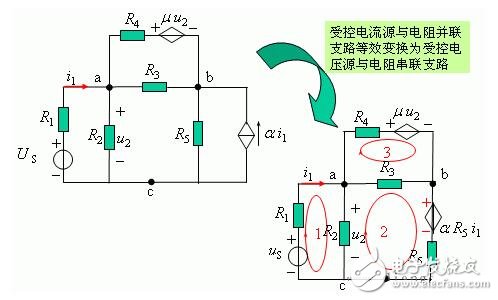
　　方程列写分两步：

　　（1）先将受控源看作独立源列方程；

　　（2）将控制量用未知量表示，并代入（1）中所列的方程，消去中间变量。

　　各回路的KVL方程：

　　

　　例14. 已知无伴电流控制电流源 id =β i2，电压控制电压源 ud = αu2，试列出该电路的回路电流方程。

　　

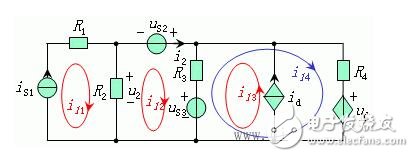
　　解：让 iS1和 id 都只有一个回路电流流过，前者为il1、后者为il3，这就可不列回路1和回路3的KVL方程。

　　

　　例15.列写下图所示电路的回路电流方程。

　　

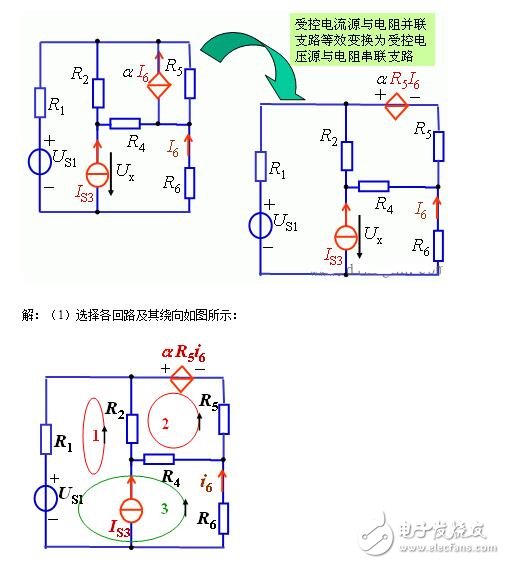
　　（2）各回路的KVL方程：

　　

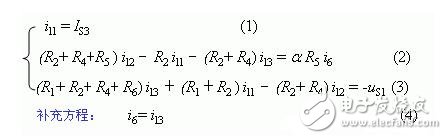
　　例16

　　

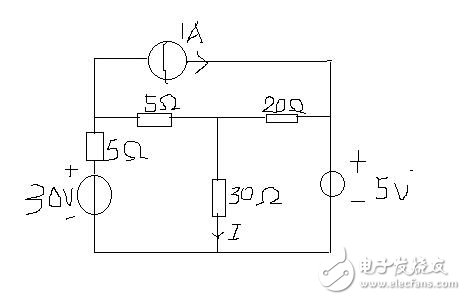
　　解：最上边和下边两个网孔分别设三个回路电流I1 I2 I3 均为顺时针设电流源两侧电压为U左正右负

　　列方程为

　　（5+20）*I1-5*I2-20*I3+U=0

　　（5+5+30）*I2-5*I1-30*I3=30

　　50*I3-20*I1-30*I2=-5

　　补充方程

　　I1=1A

　　解就行了

　　I=I2-I3

　　解得I2=2A I3=1.5A

　　I=0.5A

　　例17：网孔电流法例题

　　

　　

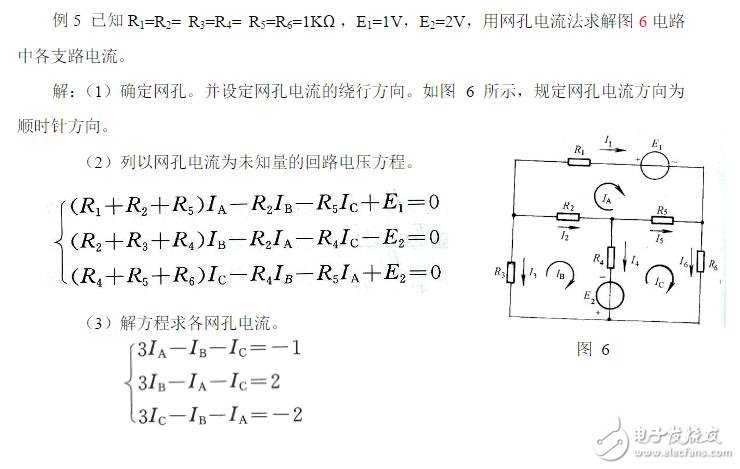
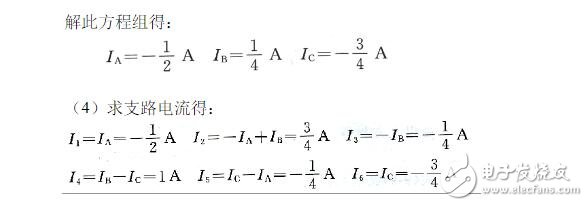
　　（5）验算。列外围电路电压方程验证。

　　由上面的例子可以看出，网孔电流法的解题思想，就是用较少的方程求解多支路电路的支路电流。先以回路电流为未知量，列出以电流为未知量的网孔电压方程，再求解支路电流。要注意的是，列回路电压方程时，回路电流的方向，要以自身回路电流方向为参考。电动势的方向也要依据回路电流方向。然后求解支路电流时，要以支路电流方向为参考。

　　但是可以发现如果网孔较多的话，同样存在方程数量过多，解题繁琐的问题。