开发中虚函数应用，大大减少开发时间

近日周立功教授公开了数年的心血之作《程序设计与数据结构》，电子版已无偿性分享到电子工程师与高校群体下载，经周立功教授授权，特对本书内容进行连载。

>>>> 1.1 虚函数

>>> 1.1.1 二叉树

树的应用非常广泛，比如，数据库就是由树构造而成的，C编译器的词法分析器也是经过语法分析生成的树。

树是一种管理象树干、树枝、树叶一样关系的数据的数据结构，通常一棵树由根部长出一个树干，接着从树干长出一些树枝，然后树枝上又长出更小的树枝，而叶子则长在最细的树枝上，树这种数据结构正是象一棵树倒过来的树木。

树是由结点（顶点）和枝构成的，由一个结点作为起点，这个起点称为树的根结点。从根结点上可以连出几条枝，每条枝都和一个结点相连，延伸出来的这些结点又可以继续通过枝延伸出新的结点。这个过程中的旧结点称作父结点，而延伸出来的新结点称作子结点，一个子结点都没有的结点就叫做叶子结点。另外，从根结点出发到达某个结点所要经过的枝的个数叫做这个结点的深度。

从家谱树血缘关系来看，家谱树使得介绍计算机科学中用于描述树结构的术语变得更简单了。树中的每一个结点都可以有几个孩子，但是只有一个双亲。在树中祖先和孙子的意义与日常语言中的意义完全相同。

与根形成对比的是没有孩子的结点，这些结点称为叶，而既不是根又不是叶的结点称为内部结点，树的长度定义为从根到叶的最长路径的长度（或深度）。在一颗树里，如果从根到叶的每条路径的长度都大致相等，那么这颗树被称为平衡树。实际上，要实现某种永远能够保证平衡的树是很复杂的，这也是为什么存在多种不同种类的树的原因。

实际上，在树的每一层次都是分叉形式，如果任意选取树中的一个结点和它的子树，所得到的部分都符合树的定义。树中的每个结点都可以看成是以它自己为根的子树的根，这就是树结构的递归特性。如果以递归的观点考察树，那么树只是一个结点和一个附着其上的子树的集合——在叶结点的情景下该集合为空，因此树的递归特性是其底层表示和大部分针对树操作的算法的基础。

树的一个重要的子类是二叉树，二叉树是一种常用的树形数据结构。二叉树的每个结点最多只有两个子结点（left和right），且除了根以外的其它结点，要么是双亲结点的左孩子，要么是右孩子。

>>> 1.1.2 表达式算术树

1. 问题

求解算术表达式就是一种二叉树，它的结点包含两种类型的对象：操作符和终值。操作符是拥有操作数的对象，终值是没有操作数的对象。表达式树背后的思想——存储在父结点中的是操作符，其操作数是由子结点延伸的子树组成的。操作数有可能是终值，或它们本身也可能是其它的表达式。表达式在子树中展开，终值驻留在叶子结点中，这种组织形式的好处是可以通过表达式将一个表达式转换为3种常见的表示形式：前缀、中缀和后缀，但中缀表达式是在数学中学到的最为熟悉的表达方式。在这里，将以2*（3+4）+5中缀表达式算术树结构为例。

首先将“2*（3+4）+5”拆分为左子树和右子树，其中，“+” 为根节点，左子树的值为2*（3+4），右子树的值为5；接着将2*(3+4)拆分为左子树和右子树，其中，“*”为根节点，左子树的值为2，右子树的值为3+4；然后将3+4拆分为左子树和右子树，其中，“+”为根节点，左子树的值为3，右子树的值为4，详见图 4.6。注意，树的表示法中不需要任何小括号或运算符优先级的知识，因为它描述的计算过程是唯一的。

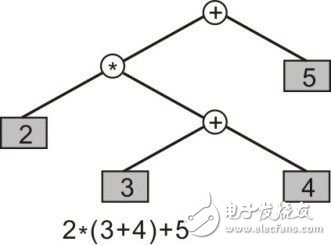
图 4.6 表达式算术树

由此可见，从根结点（Node）到叶进行分析，该表达式算术树的结点是算术运算符“+（Additive）”和“*（Multiplicative）”，它的树叶是操作数（Number）。由于这里所有的操作都是二元（Binary）的，即每个结点最多只有两个孩子，这颗特定的树正好是二叉树。因此可以用以下方式计算（calculate，简写为calc）每个结点：

● 如果是一个数字，则返回它的值；

● 如果是一个运算符，则计算左子树和右子树的值。

其计算过程是先分别输入3和4，接着计算3+4；然后输入2，再接着计算2*(3+4)；接着输入5，最后计算2*(3+4)+5。

传统的做法是定义一个struct _Node，包含二元运算符和数字结点，详见程序清单 4.12。

程序清单 4.12 表达式算术树接口（calctree.h）

1    #pragma once 

2

3    #define NUM_NODE    1 

4    #define ADD_NODE     2 

5    #define MULT_NODE  3

6

7    typedef struct _Node{

8         int type;

9         double val;

10        struct _Node *pLeft; 

11        struct _Node *pRight; 

12  }Node; 

13

14  double Calc(Node * pNode); 

15

16  #define newNumNode(val) {NUM_NODE, (val), NULL, NULL}; 

17  #define newAddNode(pLeft, pRight) {ADD_NODE, 0, (pLeft), (pRight)}; 

18  #define newMultNode(pLeft, pRight) {MULT_NODE, 0 , (pLeft), (pRight)}; 

其中，使用了名为newNumNode、newAddNode和newMultNode的宏将结构体初始化，表达式算术树接口的实现详见程序清单 4.13。

程序清单 4.13 表达式算术树接口的实现（cacltree.c）

1    #include"Node.h" 

2

3    double Calc(Node * pNode)

4    { 

5         double x = 0; 

6         switch (pNode -> type){ 

7         case NUM_NODE:

8               x = pNode -> val;

9               break; 

10        case ADD_NODE:

11             x = Calc(pNode -> pLeft) + Calc(pNode -> pRight); 

12             break; 

13        case MULT_NODE: 

14             x = Calc(pNode -> pLeft) * Calc(pNode -> pRight);

15             break; 

16        default:

17             break;

18        } 

19        return x;

20  }

表达式算术树的使用范例详见程序清单 4.14。

程序清单 4.14 表达式算术树使用范例

1    #include

2    #include "Node.h"

3

4    void main() 

5    {

6         Node node1 = newNumNode(20.0);

7         Node node2 = newNumNode(-10.0);

8         Node node3 = newAddNode(&node1, &node2);

9         Node node4 = newNumNode(0.1);

10        Node node5 = newMultNode(&node3, &node4);

11        printf("Calculating the tree\n"); 

12        double x = Calc(&node5); 

13        printf("Result:%lf\n", x); 

14  } 

2. 抽象类

根据问题的描述，需求词汇表中有一组这样的概念，比如，根结点和左右叶子结点的操作数，且加法和乘法都是二元操作。虽然词汇表对应的词汇为Node、_pLeft、_pRight、Number、Binary、Additive和Multiplicative，但用Node、_pLeft、_pRight、NumNode、BinNode、AddNode和MultNode描述表达式算术树的各个结点更准确。

由于AddNode和MultNode都是二元操作，其共性是两个数（_pLeft和_pRight）的计算，其可变性分别为加法和乘法，因此可以将它们的共性包含在BinNode中，可变性分别包含在AddNode和MultNode中。

其实输入操作数同样可以视为计算，因此NumNode和BinNode的共性也是计算，不妨将它们的共性上移到Node抽象类中。

显然，基于面向对象的C编程，则表达式算术树的所有结点都是从类Node继承的子类，Node的直系后代为NumNode和BinNode，NumNode表示一个数，BinNode表示一个二元运算，然后再从BinNode派生两个类：AddNode和MultNode。

如图 4.7所示展示了类的层次性，它们是一种“is-a”的抽象层次结构，子类AddNode和MultNode重新定义了BinNode和Node基类的结构和行为。基类代表了一般化的抽象，子类代表了特殊的抽象。虽然抽象类Node或BinNode不能实例化，只能作为其它类的父类，但NumNode、AddNode和MultNode子类是可以实例化的。

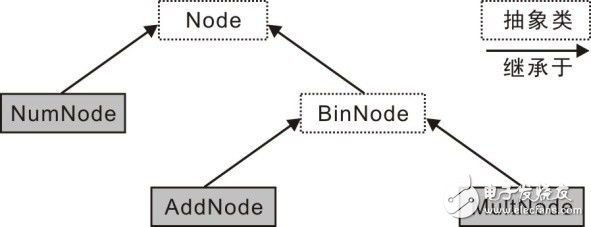
图 4.7 结点的类层次

Node抽象类的定义如下：

1    typedef struct _Node{ 

2         double (*nodeCalc)(struct _Node *pThis); 

3    }Node; 

除了Node之外，每个子类都要实现自己的nodeCalc计算方法，并返回一个作为计算结点值的双精度数。即：

1    typedef struct _NumNode{ 

2          Node       isa; 

3          double     _num;

4    }NumNode;

5

6    typedef struct _BinNode{

7          Node     isa; 

8          Node  *_pLeft; 

9          Node  *_pRight;

10  }BinNode;

11

12  typedef struct _AddNode{ 

13        BinNode   isa; 

14  }AddNode; 

15

16  typedef struct _MultNode{

17        BinNode   isa;

18  }MultNode;

其中的NumNode结点是从Node分出来的，_num表示数值。BinNode也是从Node分出来的，_pLeft和_pRight分别为指向左子树和右子树的指针，而AddNode和MultNode又是从BinNode分出来的。

此前，针对继承和多态框架，使用了一种称为静态的初始化范型。在这里，将使用动态内存分配初始化范型处理继承和多态框架。

3.建立接口

由于对象不同，因此动态分配内存的方式不一样，但其共性是——不再使用某个对象时，释放动态内存的方法是一样，因此还需要添加一个node_cleanup()函数，这是通过free()实现的，详见程序清单 4.15。

程序清单 4.15 表达式算术树的接口（CalcTree1.h）

1    #pragma once

2    typedef struct _Node Node;

3    typedef double (*node_calc_t)(Node *pThis);

4    typedef void (*node_cleanup_t)(Node *pThis); 

5    struct _Node{

6          node_calc_t    node_calc;

7          node_cleanup_t    node_cleanup; 

8    };

9

10  typedef struct _NumNode{

11        Node       isa; 

12        double     _num; 

13  }NumNode;

14

15  typedef struct _BinNode{

16        Node        isa; 

17        Node       *_pLeft;

18        Node       *_pRight; 

19  }BinNode;

20

21  typedef struct _AddNode{

22        BinNode   isa; 

23  }AddNode;

24

25  typedef struct _MultNode{ 

26        BinNode   isa; 

27  }MultNode; 

28

29  NumNode * newNumNode(double num); 

30  double node_calc(Node *pThis);

31  AddNode * newAddNode(Node *pLeft, Node *pRight); 

32  MultNode * newMultNode(Node *pLeft, Node *pRight); 

33  void node_cleanup(Node *pThis);

实现表达式算术树的第一步是输入数据和初始化NumNode结构体的变量isa和_num，newNumNode()函数原型如下：

NumNode * newNumNode(double num); 

其调用形式如下：

Node * pNode1 = (Node *)newNumNode(20.0); 

Node * pNode2 = (Node *)newNumNode(-10.0);

接下来开始为计算做准备，node_calc()函数原型如下：

double node_calc(Node *pThis);

其调用形式如下：

node_calc(pNode1);

然后开始进行加法运算，newAddNode()函数原型如下：

AddNode * newAddNode(Node *pLeft, Node *pRight); 

其调用形式如下：

Node * pNode3 = (Node *)newAddNode(pNode1, pNode2);

当然，也可以开始进行乘法运算了，newMultNode()函数原型如下：

MultNode * newMultNode(Node *pLeft, Node *pRight); 

其调用形式如下：

Node * pNode4 = (Node *)newNumNode(0.1);

Node * pNode5 = (Node *)newMultNode(pNode3, pNode4); 

一切准备就绪，则计算最终结果并释放不再使用的资源，node_cleanup()函数原型如下：

void node_cleanup(Node *pThis);

其调用形式如下：

printf("Calculating the tree\n");  

double x = node_calc(pNode5);

printf("Result:%lf\n", x); 

node_cleanup(pNode5);

4. 实现接口

显然，为每个结点创建了相应的类后，就可以为每个结点创建一个动态变量，即可在运行时根据需要使用malloc()分配内存并使用指针存储该地址，并使用指针初始化结构体的各个成员，CalcTree1.c接口的实现详见程序清单 4.16。

程序清单 4.16表达式算术树接口的实现（CalcTree1.c）

1    #include

2    #include  

3    #include " CalcTree1.h " 

4

5    NumNode * newNumNode(double num) 

6    { 

7          NumNode *pNumNode = malloc(sizeof(NumNode));

8         if(pNumNode != NULL){

9               pNumNode -> isa.node_calc = _numnode_calc;

10              pNumNode -> isa.node_cleanup = _numnode_cleanup; 

11              pNumNode -> _num = num;

12        } 

13        return pNumNode;

14  } 

15

16  static double _numnode_calc(Node *pThis) 

17  { 

18        printf("numeric node %lf\n", ((NumNode *) pThis) -> _num); 

19        return ((NumNode *)pThis) -> _num; 

20  } 

21

22  static void _numnode_cleanup(Node *pThis)

23  {

24        printf("NumNode cleanup\n");

25        free(pThis); 

26  }

27

28  double node_calc(Node *pThis) 

29  {

30        return pThis -> node_calc(pThis);

31  }

32

33  AddNode * newAddNode(Node *pLeft, Node *pRight)

34  {

35        AddNode *pAddNode = malloc(sizeof(AddNode)); 

36        if(pAddNode != NULL){ 

37              pAddNode -> isa.isa.node_calc =_addnode_calc;

38              pAddNode -> isa.isa.node_cleanup = _binnode_cleanup; 

39              pAddNode -> isa._pLeft = pLeft; 

40              pAddNode -> isa._pRight = pRight; 

41        }

42        return pAddNode;

43  } 

44

45  static double _addnode_calc(Node *pThis) 

46  { 

47        printf("Adding...\n"); 

48        AddNode * pAddNode = (AddNode*)pThis;

49        return node_calc(pAddNode -> isa._pLeft) + node_calc(pAddNode -> isa._pRight); 

50  }

51

52  static double _multnode_calc(Node *pThis)

53  {

54        printf("Multiplying...\n"); 

55        MultNode * pMultNode = (MultNode*)pThis; 

56        return node_calc(pMultNode -> isa._pLeft)*node_calc(pMultNode -> isa._pRight); 

57  }

58

59  static void _binnode_cleanup(Node *pThis) 

60  { 

61        printf("BinNode cleanup\n");

62        BinNode * pBinNode = (BinNode*)pThis; 

63        node_cleanup(pBinNode ->_pLeft);

64        node_cleanup(pBinNode ->_pRight);

65        free(pThis);

66  } 

67

68  MultNode * newMultNode(Node *pLeft, Node *pRight)

69  { 

70        MultNode *pMultNode = malloc(sizeof(MultNode));

71        if(pMultNode != NULL){ 

72              pMultNode -> isa.isa.node_calc = _multnode_calc; 

73              pMultNode -> isa.isa.node_cleanup = _binnode_cleanup;

74              pMultNode -> isa._pLeft = pLeft; 

75              pMultNode -> isa._pRight = pRight; 

76        }

77        return pMultNode;

78  } 

79

80  void node_cleanup(Node *pThis)

81  {

82        pThis -> node_cleanup(pThis); 

83  }

>>> 1.1.3 虚函数

虽然可以使用继承实现表达式算术树，但实现代码中的每个对象都有函数指针。如果结构体内有很多函数指针，或必须生成更多的对象时，将会出现多个对象具有相同的行为、需要较多的函数指针和需要生成较多数量的对象，将会浪费很多的内存。

不妨将Node中的成员转移到另一个结构体中实现一个虚函数表，然后在接口中创建一个抽象数据类型NodeVTable，在此基础上定义一个指向该表的指针vtable。比如：

1    // 接口（CalcTree2.h）

2    typedef  struct _NodeVTable  NodeVTable;

3    typedef struct _Node{

4         const NodeVTable * vtable; 

5    }Node;

6    // 实现（CalcTree2.c）

7    typedef double (*node_calc_t)(Node *pThis);

8    typedef void (*node_cleanup_t)(Node *pThis); 

9    struct _NodeVTable{ 

10        const node_calc_t node_calc;

11        const node_cleanup_t node_cleanup; 

12  }; 

13  const NodeVTable _addnode_vtable = { _addnode_calc, _binnode_cleanup}; 

表达式算术树的接口详见程序清单 4.17，其中的NumNode派生于Node，_num表示数值；BinNode也是派生于Node，pLeft和pRight分别表示指向左子树和右子树的指针；而AddNode和MultNode又派生于BinNode。虽然抽象类包含一个或多个纯虚函数类，但不能实例化（此类没有对象可创建），只有从一个抽象类派生的类和为所有纯虚函数提供了实现代码的类才能实例化，它们都必须提供自己的计算方法node_calc和node_cleanup。

程序清单 4.17 表达式算术树接口（CalcTree2.h）

1    #pragma once 

2

3    typedef  struct _NodeVTable  NodeVTable;

4    typedef struct _Node{ 

5         const NodeVTable * vtable;

6    }Node;

7

8    typedef struct _NumNode{ 

9         Node   isa; 

10        double  _num; 

11  }NumNode; 

12

13  typedef struct _AddNode{ 

14        Node  isa;

15        Node  *_pLeft;

16        Node  *_pRight; 

17  }AddNode;

18

19  typedef struct _MultNode{ 

20        Node  isa; 

21        Node  *_pLeft;

22        Node  *_pRight;

23  }MultNode;

24

25  double node_calc(Node *pThis); 

26  void node_cleanup(Node *pThis); 

27

28  NumNode * newNumNode(double num);

29  AddNode * newAddNode(Node *pLeft, Node *pRight); 

30  MultNode * newMultNode(Node *pLeft, Node *pRight); 

显然，为每个结点创建了相应的类后，就可以为每个结点创建一个动态变量，即可在运行时根据需要使用malloc()分配内存并使用指针存储该地址，并使用指针初始化结构体的各个成员，表达式算术树接口的实现详见程序清单 4.18。

程序清单 4.18 表达式算术树接口的实现（CalcTree2.c）

1    #include

2    #include

3    #include " CalcTree2.h "

4 

5    typedef double (*node_calc_t)(Node *pThis);

6    typedef void (*node_cleanup_t)(Node *pThis);

7    struct _NodeVTable{

8          const node_calc_t node_calc;

9          const node_cleanup_t node_cleanup;

10  };

11

12  static double _numnode_calc(Node *pThis)

13  {

14        printf("numeric node %lf\n", ((NumNode *)pThis)->_num);

15        return ((NumNode *)pThis) ->_num;

16  }

17

18  static void _numnode_cleanup(Node *pThis)

19  {

20        printf("NumNode cleanup\n");

21        free(pThis);

22  }

23

24  const NodeVTable _numnode_vtable = {_numnode_calc, _numnode_cleanup};

25

26  static void _binnode_cleanup(Node *pThis)

27  {

28        printf("BinNode cleanup\n");

29        BinNode * pBinNode = (BinNode*)pThis;

30        node_cleanup(pBinNode ->_pLeft);

31        node_cleanup(pBinNode ->_pRight);

32        free(pThis);

33  } 

34

35  static double _addnode_calc(Node *pThis)

36  {

37        printf("Adding...\n");

38        AddNode * pAddNode = (AddNode*)pThis;

39        return node_calc(pAddNode -> isa._pLeft) + node_calc(pAddNode -> isa._pRight);

40  }

41

42  const NodeVTable _addnode_vtable = { _addnode_calc, _binnode_cleanup };

43

44  static double _multnode_calc(Node *pThis)

45  {

46        printf("Multiplying...\n");

47        MultNode * pMultNode = (MultNode*)pThis;

48        return node_calc(pMultNode -> isa._pLeft)*node_calc(pMultNode -> isa._pRight);

49  }

50 

51  const NodeVTable _multnode_vtable = { _multnode_calc, _binnode_cleanup };

52

53  NumNode * newNumNode(double num) 

54  {

55        NumNode *pNumNode  = malloc(sizeof(NumNode));

56        if(pNumNode != NULL){

57              pNumNode -> isa.vtable  = &_numnode_vtable;

58              pNumNode -> _num         = num; 

59        } 

60        return pNumNode; 60        return pNumNode; 

61  } 

62

63  AddNode * newAddNode(Node *pLeft, Node *pRight) 

64  {

65        AddNode *pAddNode  = malloc(sizeof(AddNode)); 

66        if(pAddNode != NULL){ 

67              pAddNode -> isa.isa.vtable   = &_addnode_vtable;

68              pAddNode -> isa._pLeft  = pLeft;

69              pAddNode -> isa._pRight      = pRight;

70        } 

71        return pAddNode;

72  }

73

74  MultNode * newMultNode(Node *pLeft, Node *pRight)

75  { 

76        MultNode *pMultNode = malloc(sizeof(MultNode));

77        if(pMultNode != NULL){

78              pMultNode -> isa.isa.vtable   = &_multnode_vtable;

79              pMultNode -> isa._pLeft  = pLeft;

80              pMultNode -> isa._pRight  = pRight;

81        } 

82        return pMultNode;

83  } 

84

85  double node_calc(Node *pThis)

86  {

87        return pThis -> vtable -> node_calc(pThis);

88  } 

89

90  void node_cleanup(Node *pThis) 

92        pThis -> vtable -> node_cleanup(pThis); 

93  }