

艾体宝洞察 一文读懂最新密码存储方法,揭秘密码存储常见误区!
电子说
描述
在信息安全的诸多领域之中,密码的安全存储无疑已然成为最为核心的问题之一。随着攻击技术的不断演进,传统的密码存储方法已无法抵御现代复杂的威胁。更为安全、健壮的密码存储机制也成为当代信息安全从业者的关注点。本篇文章将引入并介绍密码存储中的基石,关于密码哈希、盐加密(Salting)、密钥派生函数(KDF)的原理及其应用,揭示密码存储中的常见误区,并分享一系列安全实践。
一、为什么不能使用明文存储密码
直接将密码以明文存储在数据库中无异于为攻击者打开了方便之门。一旦数据库遭遇泄露,攻击者将轻而易举地获得所有用户的明文密码。更严重的是,这些密码可能被用于其他攻击场景,尤其是“凭证填充攻击”(Credential Stuffing)。此类攻击是指攻击者利用已知的用户名和密码组合尝试登录其他系统,时至今日,许多用户仍在多个系统中重复使用同一个密码。得益于此,这类攻击在实际中往往具有极高的成功率。凭证填充攻击还可能导致极为严重的后果,从电子邮件账户的入侵到银行账户的盗窃,还有可能进一步引发连锁效应。
因此,明文存储密码在现代信息安全领域是绝对不可取的。信息安全从业者必须采用适当的哈希或加密技术讲原始密码进行处理后再存储至数据库中,即便攻击者获取了数据库中的数据,也无法轻易还原出用户的密码。
二、哈希与加密的区别:为什么密码存储需要哈希?
在密码存储的讨论中,我们首先需要明确哈希与加密的本质区别。
加密与哈希
加密是一个可逆的过程,通过特定的算法将明文转换为密文,并且在拥有正确密钥的前提下,密文可以被还原为明文。加密算法在数据传输和敏感数据保护中发挥着不可替代的作用。但与一般的认知可能恰恰相反,加密技术并不适合用于密码存储。原因在于,一旦存储密文的密钥遭到泄露,攻击者便可以通过解密操作直接恢复用户密码。鉴于此,加密在密码存储领域的应用相对有限。
哈希则是不可逆的。这意味着一旦数据经过哈希处理,理论上无法通过哈希值逆推出原始数据。哈希算法通过固定的规则对输入进行处理,并输出一个固定长度的哈希值。同样的输入必然会生成相同的输出,这使得哈希算法在验证数据一致性方面具有独特的优势。对于密码存储来说,哈希算法的不可逆性使得攻击者即便获取了哈希值,他们也无法轻易还原出原始密码。
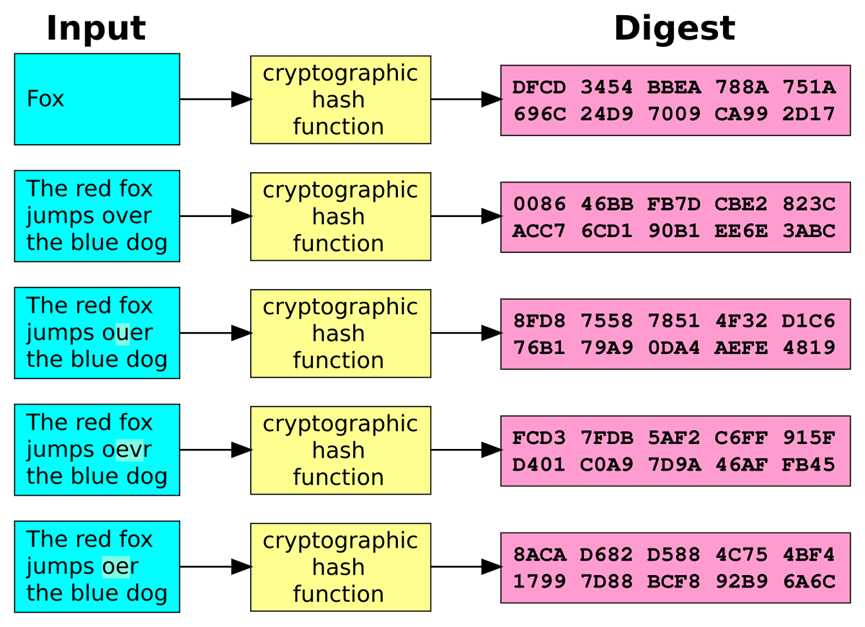
并非所有哈希算法的设计初衷并都用于安全保护。实际上大部分的哈希算法设计初衷都用于数据完整性校验。因此,在密码存储中,我们应优先选择那些针对密码存储需求特别优化的哈希函数,如密码哈希函数和密钥派生函数。
哈希算法的选择
常见的哈希算法包括 MD5、SHA1、SHA2、SHA3 等。然而,MD5 和 SHA1 已被证明具有较弱的抗碰撞性,因此不再被推荐用于密码存储。当前,推荐使用更为安全的算法,例如 SHA256 或更高级的专为密码存储设计的 KDF 算法(如 bcrypt、Argon2 等)。
常见的哈希算法包括 MD5、SHA1、SHA256 等。随着密码学领域的发展,MD5 和 SHA1 的抗碰撞性已被证明不足以抵御现代攻击,尤其是针对彩虹表(Rainbow table)攻击和碰撞攻击,这部分内容我们将在稍后讲到。因此,这些算法已不再被推荐用于密码存储。
目前,安全专家建议使用更为安全的哈希算法,SHA256 或 SHA3 都是比较好的选择。在密码存储场景中,使用专门设计的密码哈希函数则更为合适。例如,bcrypt、Argon2 和 PBKDF2 都是目前被广泛使用的密码哈希函数。其不仅能够提供比通用哈希函数更强的安全性,还具备可调的计算复杂度,能够有效抵御暴力破解攻击和硬件加速攻击(包括 GPU、ASIC 攻击等)。
三、加盐(Salt):防御彩虹表攻击的必然选择
尽管哈希算法具备不可逆性,但它们本质上是确定性的:相同的输入总会生成相同的哈希值。彩虹表是一种预计算的哈希值与对应明文的查找表,攻击者可以利用彩虹表等预计算攻击手段,轻松破解常见的密码。
为了解决这一问题,密码存储中普遍引入了“加盐”技术。盐(Salt)是一个随机生成的值,它会在密码进行哈希处理之前与密码组合。通过这种方式,即使两个用户使用了相同的密码,由于使用了不同的盐值,最终存储在数据库中的哈希值也将不同。这种策略有效抵御了彩虹表攻击,攻击者无法为每个可能的盐值与密码组合生成预计算的哈希表。
如何正确使用盐值?
盐值的使用虽然简单,但其安全性依赖于几点重要原则:
唯一性:每个用户的密码哈希都应使用不同的盐值。这样,即使两个用户选择了相同的密码,其对应的哈希值也会不同。
足够长度:盐值的长度应足够长,通常建议至少为 16 字节或更长,为盐值提供随机性和不可预测性。
安全生成:盐值必须通过安全的随机数生成器生成,避免使用伪随机数生成器(PRNG),伪随机数可能会导致盐值的可预测性,进而削弱安全性。
知其原理,而在我们实际的开发过程中,目前主流的编程语言与安全框架均已集成成熟的盐值算法库,按需调用即可。
四、密钥派生函数(KDF):密码存储的坚实防线
虽然加盐哈希在抵御彩虹表攻击上有显著效果,但它并不能完全防止暴力破解等其他形式的攻击。攻击者可以通过持续尝试可能的密码组合,最终得出正确的密码。因此,进一步增强密码存储的安全性成为当务之急,这就引入了密钥派生函数(Key Derivation Function,KDF)。
什么是 KDF?
KDF 是一种增强版的哈希函数,其核心目的是通过增加计算成本来阻止攻击者的暴力破解。与标准哈希函数相比,KDF 的工作原理是通过反复多次迭代原始输入(通常会包括密码和盐值),从而使得每次哈希计算都更加耗时和资源密集。通过这种方式,KDF 有效地增加了密码哈希计算的难度和时间,使得即便拥有强大计算能力的攻击者也无法快速破解密码。
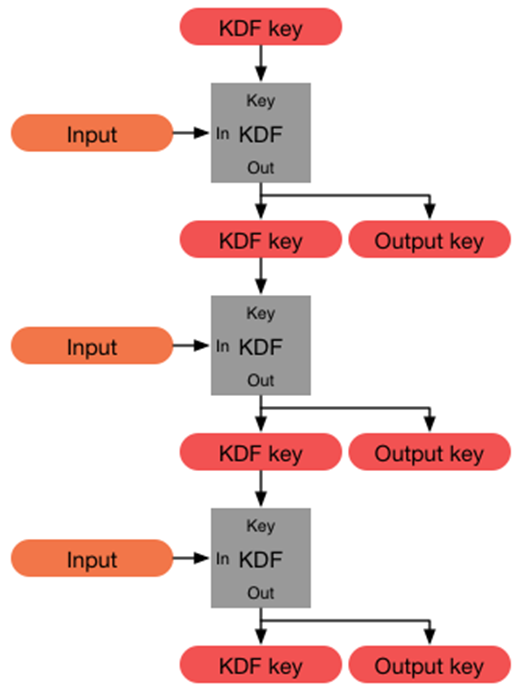
常见的 KDF 算法包括上述提及的 bcrypt、PBKDF2 和 Argon2。这类算法就是专门设计用于提高密码存储的安全性,不仅增加了计算复杂度,还可以通过调整参数来平衡安全性与性能之间的关系。
Argon2 的优势
Argon2 值得独自拿来说一下。作为近年来最为推荐的 KDF 算法之一,Argon2 在 2015 年密码学竞赛中获得了最高奖项。Argon2 被设计为可以抵抗现代硬件加速的暴力破解攻击,特别是在 GPU、FPGA 和 ASIC 等硬件上,其通过增加内存消耗使得这些攻击的实施变得更加困难。
Argon2 有三个版本:Argon2d 侧重于抗 GPU 并行攻击,Argon2i 侧重于抗时间侧信道攻击,而 Argon2id 则结合了两者的优点,通常被认为是密码存储的最佳选择。通过合理调整 Argon2 的内存和计算参数,可以根据实际需求实现较好的安全性与性能平衡,在对抗现代攻击手段方面表现尤为出色。
五、彩虹表攻击
彩虹表攻击是一种通过查找预计算哈希值来破解密码的技术。攻击者会生成一个包含大量常见密码及其哈希值的查找表,随后将这些哈希值与数据库中的密码哈希进行匹配,从而快速找出对应的明文密码。该攻击方法特别适用于使用弱密码且未进行加盐处理的系统。
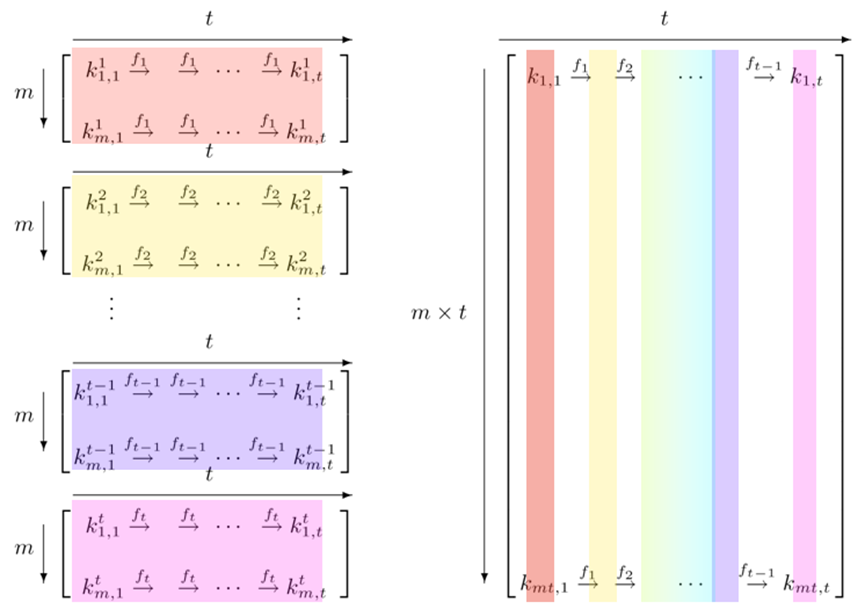
相对地,彩虹表的有效性极大地依赖于预计算的范围和密码的复杂性。通过引入“加盐(Salt)”技术,每个密码在哈希处理前加入一个独特的随机盐值,这意味着即便两个用户使用相同的密码,最终生成的哈希值也会完全不同。由于盐值的随机性,攻击者很难为每种盐值与密码组合生成彩虹表,从而有效地抵御此类攻击。
六、MD5 和 SHA1:为何不再安全?
曾几何时,MD5 和 SHA1 是广泛应用于密码存储和数据完整性校验的常用算法。然而,随着计算能力的提升和密码学研究的深入,这两种算法的弱点逐渐暴露,尤其是在抗碰撞性方面的不足,使得它们在当今的安全场景中不再适用。
MD5:早在 2004 年,研究人员就已发现了 MD5 的严重碰撞漏洞。碰撞攻击的出现使得攻击者可以生成两个不同的输入,它们具有相同的哈希值,从而削弱了 MD5 的安全性。
SHA1:2017 年,Google 公开了一种有效的碰撞攻击方法,证明 SHA1 的安全性已经不再足够强大。由于碰撞攻击的成本显著降低,SHA1 逐渐退出了密码存储和数据完整性验证的主流应用。
目前,在密码存储和数据完整性验证中,建议使用更为安全的哈希算法,如 SHA256 和 SHA3,它们在抗碰撞性和抗暴力破解方面提供了更强的保障。此外,上文中提到的 KDF 也不失为一种较好的选择。
七、密码存储的最佳实践
为了确保密码存储的安全性,安全行业有着以下公开的最佳实践,这些实践已经得到广泛采用,并应用于各类安全敏感的系统中:
永远不要以明文形式存储密码。这是密码存储中的基本原则,一旦数据库泄漏,将给系统中的用户信息带来灾难性后果。
使用强哈希算法或 KDF。推荐使用如 Argon2、bcrypt 或 PBKDF2 这样的专用密码哈希函数,以提高暴力破解的难度。
为每个密码使用唯一的盐值。即使多个用户使用相同的密码,生成的哈希值也是唯一的,防止彩虹表攻击。
避免使用已被证明不安全的算法。如 MD5和SHA1等算法已不再适用于密码存储,应选择更为安全的替代方案。
定期审查和更新密码存储策略。密码存储的安全性并非一劳永逸,随着攻击技术的进步,持续跟踪密码学领域的最新发展,并对系统进行相应的调整,才是确保安全的长久之策。
结语
密码存储的安全性直接关系到整个系统的安全。随着现代攻击手段的不断升级,采用合理的加盐哈希技术、密钥派生函数,并定期更新安全策略,才能有效降低数据泄露的风险,保障用户的隐私与安全。在这个动态变化的领域中,持续的学习与实践是每一个安全从业者的必修课。
了解网络安全更多信息,欢迎前往【艾体宝】官方网站
审核编辑 黄宇
-
电子密码锁2012-07-26 4152
-
求4*4数字密码锁的C程序2012-12-24 2243
-
单片机密码锁设计资料2013-04-01 8670
-
数码管电子密码锁2014-10-24 11854
-
急急急!!!求C语言编写的单片机电子密码锁程序2015-04-18 3341
-
超全面!破解window开机密码的方法!2016-06-03 4980
-
基于51单片机的密码锁2016-10-18 13270
-
教你如何修改NAS网络存储中的用户密码2021-02-01 6495
-
有没有方法在不使用STM32H7的情况下更新下一个电源周期可用的密码运行时间呢?2022-12-22 460
-
i.MX6ULL ---- ElfBoard 的ELF1 板卡重新烧写完成后带默认密码的方法2023-10-20 1244
-
基于明文长度的构建椭圆曲线密码密文的方法2018-01-02 1229
-
账号密码存储生成2022-11-23 662
-
NAS重置密码攻略来袭,让你告别‘密码焦虑’!2024-12-11 2069
-
走进华工科技中试基地探索科技成果转化创新密码2025-02-10 760
-
探秘智慧路灯网络安全监测,解锁城市安全新密码2025-06-27 702
全部0条评论

快来发表一下你的评论吧 !

