

matlab小波分析工具箱使用教程
matlab实验
描述
小波工具箱简介
小波工具箱包含了图像化的工具和命令行函数,它可以实现如下功能: l 测试、探索小波和小波包的特性 l 测试信号的统计特性和信号的组分 l 对一维信号执行连续小波变换
l 对一维、二维信号执行离散小波分析和综合
l 对一维、二维信号执行小波包分解(参见帮助Using Wavelet Packets) l 对信号或图像进行压缩、去噪
另外,工具箱使用户更方便的展示数据。用户可以做如下选择: l 显示哪个信号 l 放大感兴趣的区域
l 配色设计来显示小波系数细节
工具箱可以方便的导入、导出信息到磁盘或matlab工作空间。
一维连续小波分析
这一部分来测试连续小波分析的特性。连续小波分析只需要一个小波函数cwt。在这一部分将学到如下内容: l 加载信号
l 对信号执行连续小波变换
l 绘制小波系数
l 绘制指定尺度的小波系数 l 绘制整个尺度小波系数中的最大值 l 选择显示方式
l 在尺度和伪频率之间切换 l 细节放大
l 在普通或绝对模式下显示系数 l 选择执行小波分析的尺度
使用命令行执行连续小波分析
这个例子是一个包含噪声的正弦波
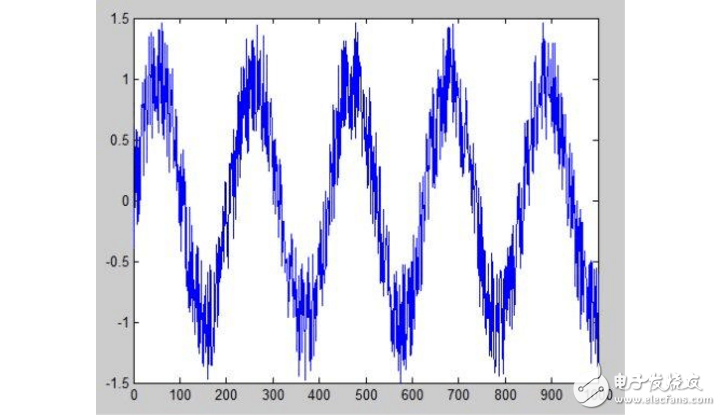
1. 加载信号
load noissin
可以使用whos显示信号信息
whos

2. 执行连续小波变换 c = cwt(noissin,1:48,‘db4’);
函数cwt的参数分别为分析的信号、分析的尺度和使用的小波。返回值c包含了在各尺度下的小波系数。对于这里,c是一个48x1000的矩阵,每一行与一个尺度相关。
3. 绘制小波系数
cwt函数可以接受第四个参数,来指定函数在执行结束后是否绘制连续小波变换系数的绝对值。另外还可以接受更多的参数来定义显示的不同特性,详见cwt函数。如下面的语句绘制系数结果
c = cwt(noissin,1:48,‘db4’,‘plot’);
4. 选择分析的尺度
cwt函数的第二个参数可以设定任意小波分析的尺度,只要这些尺度满足如下要求 l 所有尺幅必须为正实数 l 尺度的增量必须为正
l 最高的尺度不能超过由信号决定的一个最大值 如下面的代码可以执行从2开始的偶数尺度计算 c = cwt(noissin,2:2:128,‘db4’,‘plot’); 显示结果如下
这幅图像很明确的表示出了信号的周期性。
使用图形接口做连续小波分析
1. 开启一维连续小波工具,只需输入如下命令 wavemenu
出现如下小波工具箱主菜单
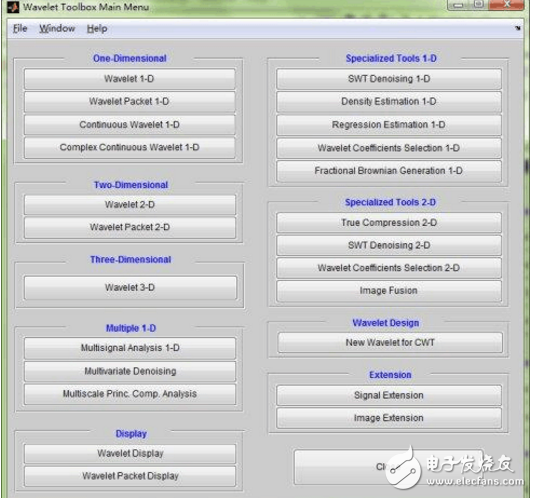
选择Continuous Wavelet 1-D菜单项,出现如下一维信号分析连续小波分析工具
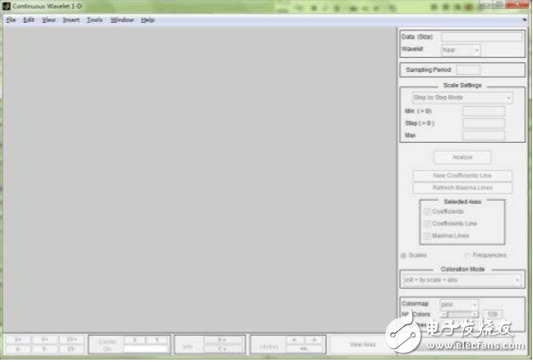
2. 加载信号
选择菜单File-》Load Signal,在Load Signal对话框里选择noissin.mat文件,它在matlab安装目录的toolbox/wavelet/wavedemo文件夹下,点击OK加载信号。
一维连续小波工具开始加载信号,加载后默认采样频率为1s。
3. 执行连续小波变换
下面来测试使用db4小波对尺度1到48做小波分析,设置如下
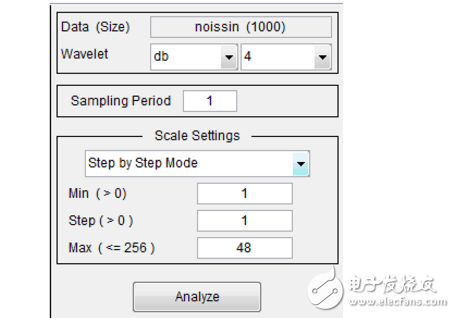
4. 点击Analyze按钮
在短暂的计算后,工具将绘制小波系数,并在Coefficients line坐标系中绘制尺度为24的小波系数,在local maxima坐标系中绘制各尺度的小波系数最大值。
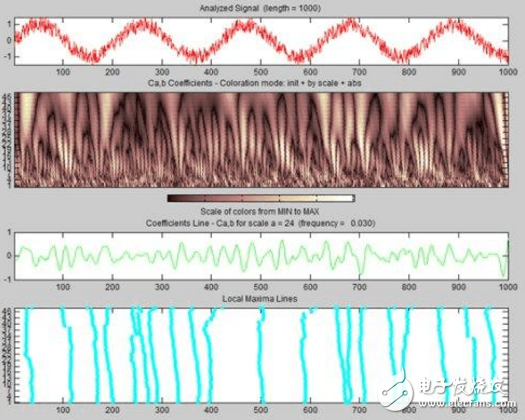
5. 查看小波Coefficients Line
在小波系数图中右键点击可以选择展示其他尺度的小波系数,选择后点击New Coefficients Line按钮,Coefficients Line会相应更新。
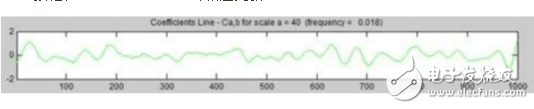
6. 查看Maxima Line
点击Refresh Maxima Line按钮,可以显示从尺度1到所选尺度的小波系数的最大值。
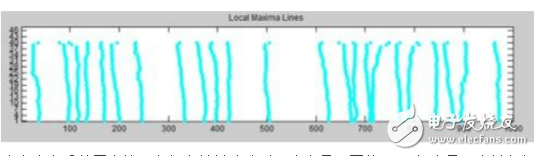
注意当在系数图中按下鼠标右键并移动时,会在最下面的Info框中显示当前鼠标位于的X位置和尺度。

7. 在尺度和伪频率之间切换
在右边选择Frequencies,当再在系数图中选择时,在Info中显示的将是Hz。

而关于尺度和频率的转换关系,可以看How to Connect Scale to Frequency?
8. 选择要显示的坐标系
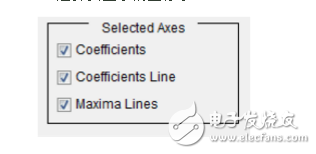
9. 放大细节
在系数框中按鼠标左键可以选择放大的范围。
10. 选择好放大范围后点击最下面的按钮可以实现指定的放大

11. 显示普通系数或系数绝对值
两种显示方式的区别在于,普通模式下,颜色映射是在系数的最大最小之间;而绝对模式,颜色映射是在0和最大的系数绝对值之间。
图形接口的导入导出信息
导入信号到一维连续小波工具
首先将要处理的信号保存到mat文件中,要求信号是一维的向量。然后使用工具的File -》Load Signal菜单功能,选择此信号文件即可导入信号。
文件中第一个一维变量被认为是信号,变量在文件中顺序是按字母排序的。
保存小波系数
小波分析完成后,点击File-》Save-》Coefficients,可以将分析结果保存到mat文件。保存后,可以使用load函数加载数据,会看到保存的变量有小波系数coeff、尺度scales、小波的名字wname。
-
matlab神经网络工具箱结果分析2024-07-03 1584
-
MATLAB自动驾驶工具箱使用2023-06-07 656
-
MATLAB小波分析高级技术2017-11-08 4412
-
matlab模糊控制工具箱的使用2016-05-04 790
-
matlab时频分析工具箱 经典模态分析EMD工具箱2015-12-03 12367
-
MATLAB_HMM工具箱2014-12-15 695
-
matlab遗传工具箱2012-05-05 4989
-
如何在labview中调用matlab的小波分析工具箱2011-03-30 7201
-
基于Matlab遗传工具箱的高强混凝土配合比优化2010-05-04 614
-
matlab常用的工具箱2010-02-08 621
-
MATLAB语言工具箱-ToolBox实用指南2009-11-25 56037
-
matlab的其他工具箱及SIMULINK2009-09-03 686
-
matlab遗传工具箱下载2008-06-18 591
全部0条评论

快来发表一下你的评论吧 !

