小波变换和小波分析的区别

　　傅立叶变换：将时域上的波形分解成正弦波的过程就是傅立叶变换，傅立叶正变换可以将波形分解，投影到频域上，傅立叶逆变换可以将频域上波形叠加，映射到时域上。变换过程如下图所示：

　　

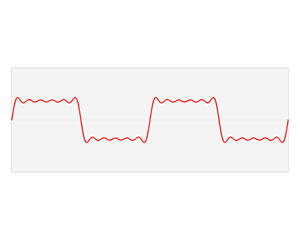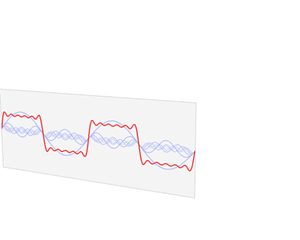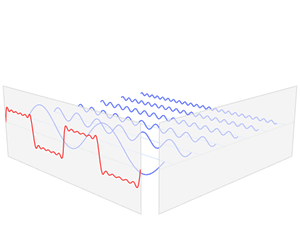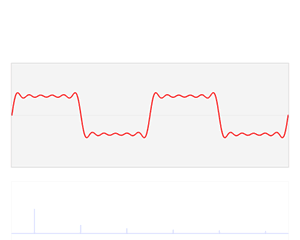
　　为何要进行傅立叶变换？

　　很多在时域看似不可能做到的数学操作，在频域相反很容易。这就是需要傅里叶变换的地方。尤其是从某条曲线中去除一些特定的频率成分，这在工程上称为滤波，是信号处理最重要的概念之一，只有在频域才能轻松的做到。离散傅里叶变换（DFT）是傅里叶变换在离散系统中的表示形式。但是DFT的计算量非常大， FFT就是DFT的一种快速算法。

　　时域分析与频域分析是对模拟信号的两个观察面，根据傅立叶分析，所有的波形都可以分解为正弦波，可以由不同频率的正弦波叠加而成，一种频率的正弦波在频域上对应一个点，就行时域上的时间点一样。例如下图波形，从时域上看是类似方波，二如果从频域上看就是一个个线段。

　　

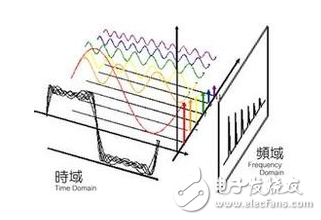
　　傅里叶变换的特点：

　　对于数据信号的去噪，傅立叶变换是将信号完全的放在频率域中分析，但无法给出信号在每一个时间点的变化情况，无论信号在时间轴上任何一点产生突变，都将会影响到整个频域的信号。因此，傅立叶变换不能有效的区分出信号中出现的尖峰是由突变部分还是不平稳白噪声引起的。

　　小波变换

　　那么你可能会想到，让窗口大小变起来，多做几次STFT不就可以了吗？！没错，小波变换就有着这样的思路。

　　但事实上小波并不是这么做的（关于这一点，方沁园同学的表述“小波变换就是根据算法，加不等长的窗，对每一小部分进行傅里叶变换”就不准确了。小波变换并没有采用窗的思想，更没有做傅里叶变换。）

　　至于为什么不采用可变窗的STFT呢，我认为是因为这样做冗余会太严重，STFT做不到正交化，这也是它的一大缺陷。

　　于是小波变换的出发点和STFT还是不同的。STFT是给信号加窗，分段做FFT；而小波直接把傅里叶变换的基给换了——将无限长的三角函数基换成了有限长的会衰减的小波基。这样不仅能够获取频率，还可以定位到时间了

　　小波做的改变就在于，将无限长的三角函数基换成了有限长的会衰减的小波基。这就是为什么它叫“小波”，因为是很小的一个波嘛

　　

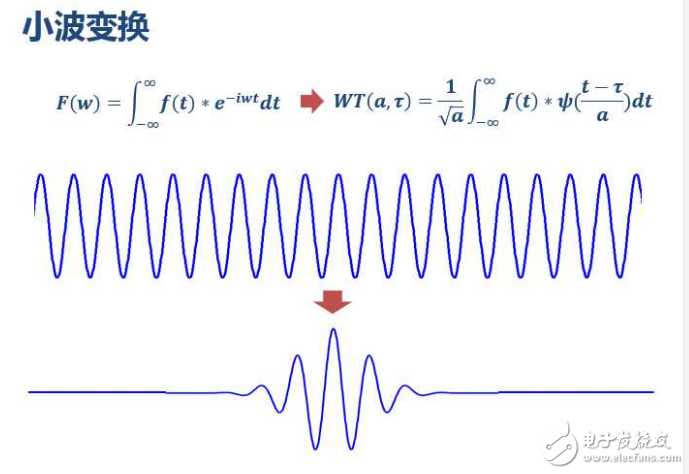
　　从公式可以看出，不同于傅里叶变换，变量只有频率ω，小波变换有两个变量：尺度a（scale）和平移量 τ（translation）。尺度a控制小波函数的伸缩，平移量 τ控制小波函数的平移。尺度就对应于频率（反比），平移量 τ就对应于时间。

　　

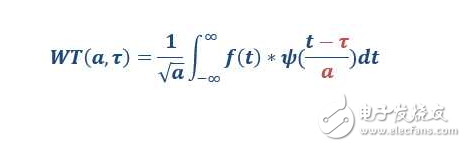
　　当伸缩、平移到这么一种重合情况时，也会相乘得到一个大的值。这时候和傅里叶变换不同的是，这不仅可以知道信号有这样频率的成分，而且知道它在时域上存在的具体位置。

　　而当我们在每个尺度下都平移着和信号乘过一遍后，我们就知道信号在每个位置都包含哪些频率成分。

　　看到了吗？有了小波，我们从此再也不害怕非稳定信号啦！从此可以做时频分析啦！

　

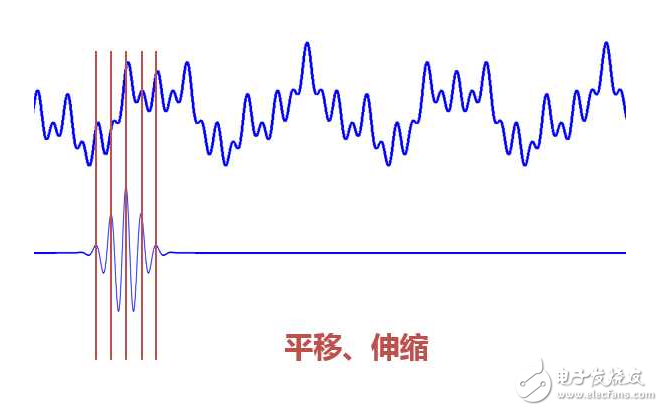
　　小波变换的特点

　　小波变换是以某些特定的函数为基，将数据信号展开成级数系列，它是空间（时间）和频率的局部变换，因此，小波变换可同时在时域和频域中对数据信号进行多尺度联合分析，从而能有效地从信号中提取信息。对于数据信号的去噪，由于小波分析可以同时在时域和频域中对信号进行联合分析，并且它具有多尺度细化分析的功能。因此，我们可以在不同的分解层上和不同的小波基函数下对信号的突变部分和噪声进行有效的区分，从而实现信号的消噪。