fft算法是什么_如何提高fft算法分辨率

　　fft算法是什么

　　FFT算法（fast Fourier transform），即快速傅里叶变换，是指利用计算机计算离散傅里叶变换（DFT）的高效、快速计算方法的统称，简称FFT。快速傅里叶变换是1965年由J.W.库利和T.W.图基提出的。采用这种算法能使计算机计算离散傅里叶变换所需要的乘法次数大为减少，特别是被变换的抽样点数N越多，FFT算法计算量的节省就越显著。

　　

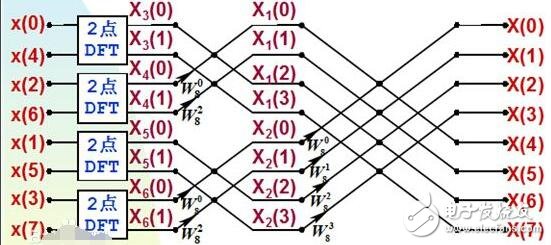
　　概念

　　有限长序列可以通过离散傅里叶变换（DFT）将其频域也离散化成有限长序列。但其计算量太大，很难实时地处理问题，因此引出了快速傅里叶变换（FFT）。 1965年，Cooley和Tukey提出了计算离散傅里叶变换（DFT）的快速算法，将DFT的运算量减少了几个数量级。从此，对快速傅里叶变换（FFT）算法的研究便不断深入，数字信号处理这门新兴学科也随FFT的出现和发展而迅速发展。根据对序列分解与选取方法的不同而产生了FFT的多种算法，基本算法是基2DIT和基2DIF。FFT在离散傅里叶反变换、线性卷积和线性相关等方面也有重要应用。

　　快速傅氏变换（FFT），是离散傅氏变换的快速算法，它是根据离散傅氏变换的奇、偶、虚、实等特性，对离散傅立叶变换的算法进行改进获得的。它对傅氏变换的理论并没有新的发现，但是对于在计算机系统或者说数字系统中应用离散傅立叶变换，可以说是进了一大步。

　　设x（n）为N项的复数序列，由DFT变换，任一X（m）的计算都需要N次复数乘法和N-1次复数加法，而一次复数乘法等于四次实数乘法和两次实数加法，一次复数加法等于两次实数加法，即使把一次复数乘法和一次复数加法定义成一次“运算”（四次实数乘法和四次实数加法），那么求出N项复数序列的X（m），即N点DFT变换大约就需要N^2次运算。当N=1024点甚至更多的时候，需要N2=1048576次运算，在FFT中，利用WN的周期性和对称性，把一个N项序列（设N=2k，k为正整数），分为两个N/2项的子序列，每个N/2点DFT变换需要（N/2）^2次运算，再用N次运算把两个N/2点的DFT变换组合成一个N点的DFT变换。这样变换以后，总的运算次数就变成N+2*（N/2）^2=N+N^2/2。继续上面的例子，N=1024时，总的运算次数就变成了525312次，节省了大约50%的运算量。而如果我们将这种“一分为二”的思想不断进行下去，直到分成两两一组的DFT运算单元，那么N点的DFT变换就只需要Nlog2N次的运算，N在1024点时，运算量仅有10240次，是先前的直接算法的1%，点数越多，运算量的节约就越大，这就是FFT的优越性。

　　如何提高fft算法分辨率

　　FFT程序，输入是一组复数，输出也是一组复数，想问一下输入到底应该输入什么，输出的复数的含义是什么。

　　给定一组序列的抽样值，如何用FFT确定它的频率。

　　首先，fft函数出来的应该是个复数，每一个点分实部虚部两部分。

　　假设采用1024点fft，采样频率是fs，那么第一个点对应0频率点，第512点对应的就是fs/2的频率点。　　然后从头开始找模值最大的那个点，其所对应的频率值应该就是要的基波频率了。

　　FFT是离散傅立叶变换的快速算法，可以将一个信号变换到频域。

　　有些信号在时域上是很难看出什么特征的，但是如果变换到频域之后，就很容易看出特征了。

　　这就是很多信号分析采用FFT变换的原因。

　　另外，FFT可以将一个信号的频谱提取出来，这在频谱分析方面也是经常用的。

　　虽然很多人都知道FFT是什么，可以用来做什么，怎么去做，但是却不知道FFT之后的结果是什么意思、如何决定要使用多少点来做FFT。

　　一个模拟信号，经过ADC采样之后，就变成了数字信号。

　　采样定理告诉，采样频率要大于信号频率的两倍，这些就不在此罗嗦了。

　　采样得到的数字信号，就可以做FFT变换了。

　　N个采样点，经过FFT之后，就可以得到N个点的FFT结果。

　　为了方便进行FFT运算，通常N取2的整数次方。