

fft算法以及c语言实现详情解答
编程语言及工具
描述
为什么需要FFT
第一个问题是为什么要创造FFT,简单的说,为了速度。我们承认DFT很有用,但是我们发现他的速度不是很快,1D的DFT原始算法的时间复杂度是O(n^2),这个可以通过公式观察出来,对于2D的DFT其时间复杂度是O(n^4),这个速度真的很难接受,也就是说,你计算一幅1024x768的图像时,所以找到一种快速方法的方法计算FFT势在必行。
以下为DFT公式

如何得到FFT
通过观察DFT公式,我们发现DFT计算每一项X[u]的时候都遍历了完整的x[n]所以,我们的想法就是能不能通过其他的X[u+m](m为一个整数,可正可负)得到X[u],也就是充分利用之间的计算结构来构建现在的结果,这种方法就很容易表现成迭代的形式。本文介绍基2的FFT,及离散信号x[n]的个数为2的k次方,即如果完整的离散信号中有N个信分量{x1,x2,x3.。。.xN}其中N=1《《k。
FFT的数学基础其实就是
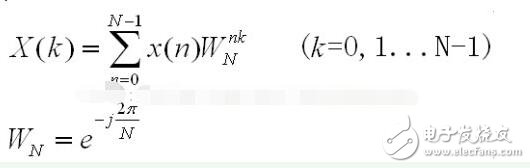
用C语言编写FFT算法
用simulink建模的方法实现FFT的问题特别多,还不如手工编写,也不是很复杂。
以下是512点的单边谱FFT算法,在TMS320C6713的DSP开发板上调试通过。下面是C语言编写FFT算法。
#include “math.h”
#define PI 3.1415926
#define SAMPLENUMBER 512
void InitForFFT();
void MakeWave();
void FFT();
int INPUT[SAMPLENUMBER],DATA[SAMPLENUMBER];
float fWaveR[SAMPLENUMBER],fWaveI[SAMPLENUMBER],w[SAMPLENUMBER];
float sin_tab[SAMPLENUMBER],cos_tab[SAMPLENUMBER];
main()
{
int i;
InitForFFT();
MakeWave();
for ( i=0;i
{
fWaveR[i]=INPUT[i];
fWaveI[i]=0.0f;
w[i]=0.0f;
}
FFT(fWaveR,fWaveI);
for ( i=0;i
{
DATA[i]=w[i];
}
while ( 1 ); // break point
}
void FFT(float dataR[SAMPLENUMBER],float dataI[SAMPLENUMBER])
{
int x0,x1,x2,x3,x4,x5,x6,x7,x8,xx;
int i,j,k,b,p,L;
float TR,TI,temp;
for ( i=0;i
{
x0=x1=x2=x3=x4=x5=x6=x7=x8=0;
x0=i&0x01; x1=(i/2)&0x01; x2=(i/4)&0x01; x3=(i/8)&0x01;x4=(i/16)&0x01; x5=(i/32)&0x01; x6=(i/64)&0x01;x7=(i/128)&0x01;x8=(i/256)&0x01;
xx=x0*256+x1*128+x2*64+x3*32+x4*16+x5*8+x6*4+x7*2+x8;
dataI[xx]=dataR[i];
}
for ( i=0;i
{
dataR[i]=dataI[i]; dataI[i]=0;
}
for ( L=1;L《=9;L++ )
{
b=1; i=L-1;
while ( i》0 )
{
b=b*2; i--;
}
for ( j=0;j《=b-1;j++ )
{
p=1; i=9-L;
while ( i》0 )
{
p=p*2; i--;
}
p=p*j;
for ( k=j;k《512;k=k+2*b )
{
TR=dataR[k]; TI=dataI[k]; temp=dataR[k+b];
dataR[k]=dataR[k]+dataR[k+b]*cos_tab[p]+dataI[k+b]*sin_tab[p];
dataI[k]=dataI[k]-dataR[k+b]*sin_tab[p]+dataI[k+b]*cos_tab[p];
dataR[k+b]=TR-dataR[k+b]*cos_tab[p]-dataI[k+b]*sin_tab[p];
dataI[k+b]=TI+temp*sin_tab[p]-dataI[k+b]*cos_tab[p];
}
}
}
for ( i=0;i
{
w[i]=sqrt(dataR[i]*dataR[i]+dataI[i]*dataI[i]);
}
}
void InitForFFT()
{
int i;
for ( i=0;i
{
sin_tab[i]=sin(PI*2*i/SAMPLENUMBER);
cos_tab[i]=cos(PI*2*i/SAMPLENUMBER);
}
}
void MakeWave()
{
int i;
for ( i=0;i
{
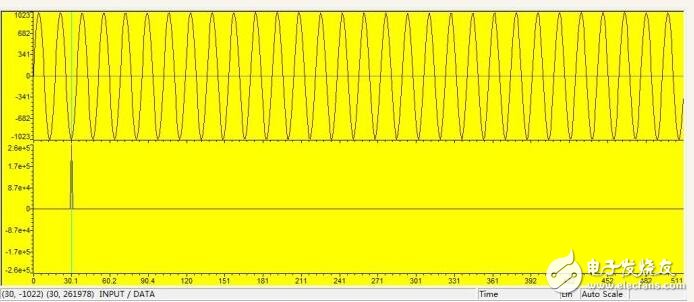
INPUT[i]=sin(PI*2*i/SAMPLENUMBER*30)*1024;
}
-
C语言实现数字信号处理算法2012-08-16 3638
-
CRC算法和c语言实现2012-08-20 4505
-
C语言实现FFT(快速傅里叶变换)2013-10-25 26459
-
PID控制算法的C语言实现(完整版)2020-04-02 5653
-
快速傅里叶变换C语言实现2021-07-20 1939
-
C语言实现常用排序算法是什么?2021-10-19 1525
-
CRC算法原理及C语言实现2009-09-23 851
-
用C语言实现DES算法2008-01-16 3375
-
用C语言实现FFT算法2008-10-30 6577
-
实数FFT算法的设计及其C语言实现2012-01-13 11254
-
DSP算法的c语言实现2016-05-09 775
-
卡尔曼滤波算法C语言实现2016-09-27 2185
-
PID控制算法的C语言实现(完整版)2016-11-05 1266
-
4个重要算法C语言实现源代码2018-06-10 1787
-
CRC校验算法原理及c语言实现2021-11-30 1112
全部0条评论

快来发表一下你的评论吧 !

