matlab小波分析步骤是什么

　　小波（Wavelet）这一术语，顾名思义，“小波”就是小的波形。所谓“小”是指它具有衰减性；而称之为“波”则是指它的波动性，其振幅正负相间的震荡形式。与Fourier变换相比，小波变换是时间（空间）频率的局部化分析，它通过伸缩平移运算对信号（函数）逐步进行多尺度细化，最终达到高频处时间细分，低频处频率细分，能自动适应时频信号分析的要求，从而可聚焦到信号的任意细节，解决了Fourier变换的困难问题，成为继Fourier变换以来在科学方法上的重大突破。

　　1、步骤

　　将原始数据文件夹copy到装有matlab 的电脑

　　打开matlab软件， 进入软件主界面

　　在软件的左下方找到start按钮，点击选择toolbox， 然后选择wavelet

　　进入wavemenu界面，选择一维小波中的wavelet1-D并 进入

　　右上角选择用于小波分析的小波基以及分解层数并点击analyse开始分析

　　选择要处理的信号，界面出现 loaded信号，这就是没有去噪前的原 始信号

　　在wavemenu主界面中选择file-load signal或者import from workspace— import signal

　　将数据文件（.Mat 格式）托到matlab 软件主界面的 workspace

　　分析后在左边栏目 中出现s，a*， d*，其中s为原信 号，a*为近似信 号，d*为细节信号

　　然后点击denoise 去噪

　　matlab小波工具箱小波分析步骤_文档下载https://www.wendangxiazai.com/b-12b70285c77da26925c5b0ae.html 阈值方法常用的有 4种fixed（固定阈值）， rigorsure， heusure，minmax 根据需要选择，一 般情况下 rigorsure方式去 噪效果较好

　　Soft（软阈值）， hard（硬阈值）一 般选择软阈值去噪 后的信号较为平滑

　　在此窗口下点击 file-save denoised singal，保存输出 去噪后的信号

　　点击denoise开始正式去噪

　　在噪声结构下面的数值不要随意改，这是系统默认的去噪幅度

　　在噪声结构中选择 unscaled white noise，因为在工程应用中的噪声一般不仅仅含有白噪 声

　　去噪结束

　　去噪结束后，把去噪后信号（.mat格 式）拖至matlab主界面的workspace 中，与原信号一起打包，以便以后计 算统计量

　　Matlab编程计算相关统计量以及特征 量

　　得出统计量和特征量后结束

　　2、步骤流程

　　

　　

　　

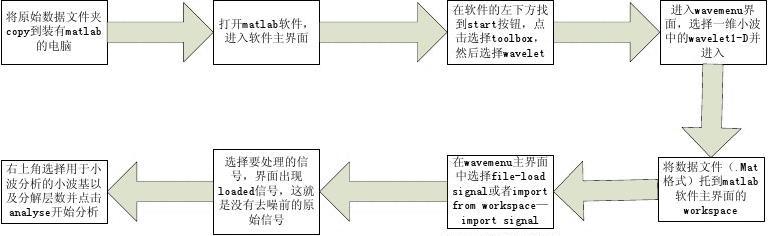
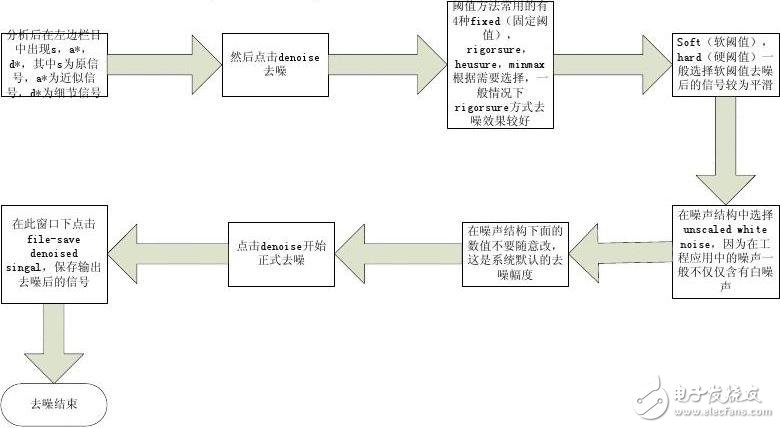
　　3、代码

　　%含噪声的三角波与正弦波的组合

　　%利用db5小波对信号进行7层分解

　　%生产正弦信号

　　clc;close all;clear all;

　　N=1000;

　　t=1:N;

　　sig1=sin（0.3*t）;

　　%生成三角形波形

　　sig2（1:500）=（（1:500）-1）/500;

　　sig2（501:N）=（1000-（501:1000））/500;

　　figure（1）;

　　subplot（211）;

　　plot（t，sig1，‘linewidth’，2）;

　　xlabel（‘样本序号 N’）;

　　ylabel（‘幅值A’）;

　　subplot（212）;

　　plot（t，sig2，‘linewidth’，2）;

　　xlabel（‘样本序号 N’）;

　　ylabel（‘幅值A’）;

　　%叠加信号

　　x=sig1+sig2+randn（1，N）;

　　figure（2）;

　　plot（t，x，‘linewidth’，2）;

　　xlabel（‘样本序号 N’）;

　　ylabel（‘幅值A’）;%一维小波分解

　　［c，l］=wavedec（x，7，‘db5’）;%重构第1-7层逼近系数

　　a7=wrcoef（‘a’，c，l，‘db5’，7）;

　　a6=wrcoef（‘a’，c，l，‘db5’，6）;

　　a5=wrcoef（‘a’，c，l，‘db5’，5）;

　　a4=wrcoef（‘a’，c，l，‘db5’，4）;

　　a3=wrcoef（‘a’，c，l，‘db5’，3）;

　　a2=wrcoef（‘a’，c，l，‘db5’，2）;

　　a1=wrcoef（‘a’，c，l，‘db5’，1）;%显示逼近系数

　　figure（3）

　　subplot（711）

　　plot（a7，‘linewidth’，2）;

　　ylabel（‘a7’）;

　　subplot（712）

　　plot（a6，‘linewidth’，2）;

　　ylabel（‘a6’）;

　　subplot（713）

　　plot（a5，‘linewidth’，2）;

　　ylabel（‘a5’）;

　　subplot（714）

　　plot（a4，‘linewidth’，2）;

　　ylabel（‘a4’）;

　　subplot（715）

　　plot（a3，‘linewidth’，2）;

　　ylabel（‘a3’）;

　　subplot（716）

　　plot（a2，‘linewidth’，2）;

　　ylabel（‘a2’）;

　　subplot（717）

　　plot（a1，‘linewidth’，2）;

　　ylabel（‘a1’）;

　　xlabel（‘样本序号 N’）;%重构第1-7层细节系数

　　d7=wrcoef（‘d’，c，l，‘db5’，7）;

　　d6=wrcoef（‘d’，c，l，‘db5’，6）;

　　d5=wrcoef（‘d’，c，l，‘db5’，5）;

　　d4=wrcoef（‘d’，c，l，‘db5’，4）;

　　d3=wrcoef（‘d’，c，l，‘db5’，3）;

　　d2=wrcoef（‘d’，c，l，‘db5’，2）;

　　d1=wrcoef（‘d’，c，l，‘db5’，1）;

　　%显示细节系数

　　figure（4）

　　subplot（711）

　　plot（d7，‘linewidth’，2）;

　　ylabel（‘d7’）;

　　subplot（712）

　　plot（d6，‘linewidth’，2）;

　　ylabel（‘d6’）;

　　subplot（713）

　　plot（d5，‘linewidth’，2）;

　　ylabel（‘d5’）;

　　subplot（714）

　　plot（d4，‘linewidth’，2）;

　　ylabel（‘d4’）;

　　subplot（715）

　　plot（d3，‘linewidth’，2）;

　　ylabel（‘d3’）;

　　subplot（716）

　　plot（d2，‘linewidth’，2）;

　　ylabel（‘d2’）;

　　subplot（717）

　　plot（d1，‘linewidth’，2）;

　　ylabel（‘d1’）;

　　xlabel（‘样本序号 N’）;