

电路时间常数怎么求
电子常识
描述
表示过渡反应的时间过程的常数。指该物理量从最大值衰减到最大值的1/e所需要的时间。对于某一按指数规律衰变的量,其幅值衰变为1/e倍时所需的时间称为时间常数。 在不同的应用领域中,时间常数也有不同的具体含义。
RC电路:t=RC;
LR电路:t=L/R;
在RC电路中,电容电压Uc总是由初始值Uc(0)按指数规律单调的衰减到零,其时间常数=R*C
在RL电路中,iL总是由初始值iL(0)按指数规律单调的衰减到零,其时间常数=L/R
现在,我们介绍几种确定时间常数的常见方法。
[方法 1]如果列出的电路方程为τdx( t) / dt + x( t) = aw( t) ( 1) 式中,x( t) 和 w( t) 分别为电路电压或电流变量和电路激励; τ 和 a 为常数,τ 就是电路的时间常数,即时间常数等于一阶电路方程特征根倒数的负值。这个方法的优点是比较直观,缺点是必须列写电路方程,求解过程显得较为复杂。
[方法 2]当一阶电路仅包含一个动态元件( 或虽包含若干个同类型的动态元件但这些动态元件可等效为一个动态元件) 时,首先求出从动态元件( 或等效动态元件) 两端看进去的等效电阻,然后可利用 τ = RC 或 τ = L /R 计算出时间常数。这是一种比较简单的计算时间常数的方法,大多数一阶电路的时间常数都可按该方法确定。
[方法 3]从式( 1) 可以看出,一阶电路的时间常数与电路的激励无关。为方便起见,在求时间常数时可将电路的激励( 电压源或电流源) 置零,然后利用 τ = RC 或 τ = L /R 就可以计算出时间常数。
[方法 4]时间常数等于一阶电路固有频率倒数的负值,因此如能求得电路的 s 域网络函数,则通过网络函数也可求得时间常数。
对于简单的一阶电路,时间常数的确定可采用上述任一方法。当一阶电路具有较复杂的形式时,则上述方法的繁简程度有较大的区别。
电路中的时间常数L/R中的R是怎么看的
简单的方法,考虑一下,戴维宁电路中等效电阻如何计算的,就知道是怎么回事了。
做法是,把动态元件移除,对剩下的一端口电路求等效电阻即可,由于剩下的一端口电路是含源网络,所以先将独立源置0(即电流源开路,电压源短路),然后对该网络求输入电阻就是要求的等效电阻!对于该问题则有Re
例子1:电路如图,求时间常数τ
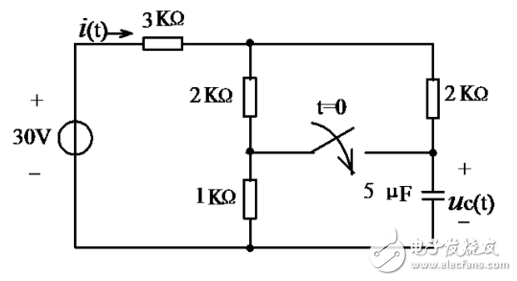
时间常数:T=ReqC
因Req=1//(2//2+3)=0.8k欧,
故T=0.8x5=4ms。
例子2:一阶电路的时间常数怎么求?求等效电阻的时候那个受控源应该怎么处理?
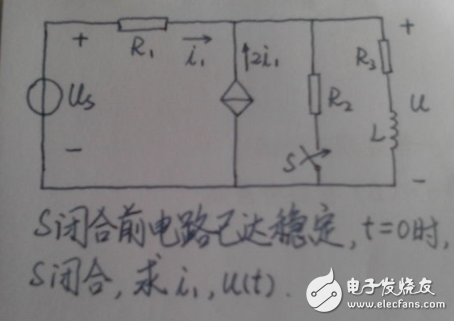
先求出等效电阻。(就是从电感哪里看进去的。)求等效电阻要先把电压源变成导线。因为有受控源,求等效电阻你只能设从L处加电压U然后求出电流I然后等效电阻就是U/I了。(或设电流求电压)
这题的等效电阻是(1/3)R1+R2×R3/(R2+R3)
然后时间常数就是L/R
例子3:时间常数怎么求?τ=RC,怎么确定r和c?图中电路的RC是怎么确定的?
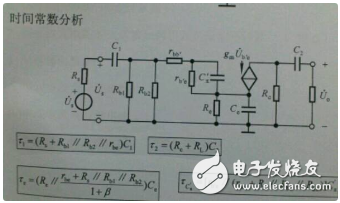
按照图中的标识,如果你要求的是Uc1(t),那么时间常数中的C就是C1的电容。同理知道其他。而时间常数中的R,有时候需要用短路法求(将电容短路,求出短路电流,再通过断路时的端电压,根据R=U/I可求。)另外一种方法是外施电源法(将电容拿掉,替换一个电源,可以是电压源,也可以是电流源,求出电流,一般是带假设的电源电压,可以约掉。)
例子4:电路时间常数怎么求
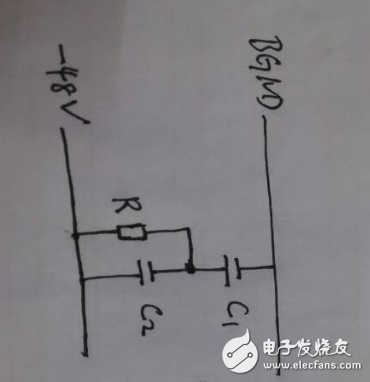
一端接电源,另一端开路?如果是这样的电源除源后求电阻两端的电容,由于电压源除源是短路,C1、C2相当于并联,所以电路的时间常数τ=R(C1+C2)
-
算时间常数时的rc单位是什么2024-09-19 9975
-
时间常数对暂态过程时间的影响有哪些2024-07-26 5492
-
电容充放电过程中时间常数对电路的影响2023-12-20 6079
-
RC时间常数的意思是什么?怎么算RC时间常数?RC时间常数的测量?2023-11-20 21192
-
什么是时间常数2021-09-13 2223
-
RC电路时间常数的定义及计算2019-04-08 19361
-
一阶电路的充放电时间常数τ2017-12-05 2496
-
rc电路时间常数的定义及计算2017-11-01 371843
-
浅谈RC电路的时间常数2010-05-30 2011
-
如何计算时间常数RC2009-08-14 16653
-
如何巧算时间常数RC2009-08-13 2751
-
常用改进时间常数的电路2009-04-08 1122
-
555常用改进时间常数的电路2008-05-19 1646
全部0条评论

快来发表一下你的评论吧 !

