字符串的KMP算法和BM算法

　　本文主要介绍KMP算法和BM算法，它们分别是前缀匹配和后缀匹配的经典算法。所谓前缀匹配是指：模式串和母串的比较从左到右，模式串的移动也是从左到右；所谓后缀匹配是指：模式串和母串的的比较从右到左，模式串的移动从左到右。看得出来前缀匹配和后缀匹配的区别就仅仅在于比较的顺序不同。下文分别从最简单的前缀蛮力匹配算法和后缀蛮力匹配算法入手，详细的介绍KMP算法和BM算法以及它们的实现。

　　KMP算法

　　首先来看一下前缀蛮力匹配算法的代码（以下代码从linux源码string.h中抠出），模式串和母串的比较是从左到右进行（strncmp（）），如果找不到和模式串相同的子串，则从左到右移动模式串，距离为1（s++）。

　　har * strstr（register const char *s， register constchar *wanted）

　　{

　　register const size_t len = strlen（wanted）;

　　if （len ==0） return （char*）s;

　　while （*s ！=* wanted || strncmp（s， wanted， len））

　　if （*s++==‘\0’）

　　return （char*）NULL;

　　return （char*）s;

　　}

　　KMP算法中的KMP分别是指三个人名：Knuth、Morris、Pratt，其本质也是前缀匹配算法，对比前缀蛮力匹配算法，区别在于它会动态调整每次模式串的移动距离，而不仅仅是加一，从而加快匹配过程。下图通过一个直观的例子展示前缀蛮力匹配算法和KMP算法的区别，前文提过，这二者唯一的不同在于模式串移动距离。

　　

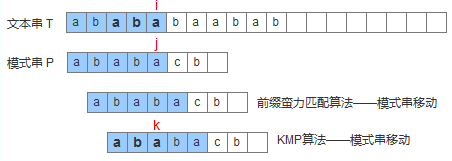
　　上图中，前缀蛮力匹配算法发现匹配不上，就向右移动距离1，而KMP算法根据已经比较过的前缀信息，了解到应该移动距离为2；换句话说针对母串的下一个匹配字符，KMP算法了解它下回应该匹配模式串的哪个位置，比如上图中，针对母串的第i+1个字符，KMP算法了解它应该匹配模式串的第k+1个字符。为什么会是这样，这是因为母串的子串T［i-k， i］=aba，而模式串的子串P［0，k］=aba，这二者正好相等。所以模式串应该移动到这个位置，从而让母串的第i+1个字符和模式串的第k+1个字符继续比较。

　　那k值又是如何寻找？请注意上图中，模式串位置j已经匹配上母串的位置i，也就是T［i-k， i］ = P［j-k， j］=aba；根据前文的T［i-k， i］ = P［0， k］ = aba， 从而得出P［0， k］ = P［j-k， j］ = aba。通过观察发现，就是在模式的子串［0， j］中寻找一个最长前缀［0，k］，从而使得［j-k， j］ = ［0，k］；

　　于是可以定义一个jump数组，jump［j］=k，表示满足P［0， k］ ==P［j-k， j］ 的最大k值，或者表述为：如果模式串j+1匹配不上母串的i+1，那跳转到模式串k+1继续比较。有了这个jump数组，就很容易写出kmp算法的伪代码：

　　j：=0;

　　for i：=1 to n do

　　Begin

　　while （j》0） and （P［j+1］《》T［i］） do j：=jump［j］;［

　　if P［j+1］=T［i］ then j：=j+1;

　　if j=m then

　　Begin

　　writeln（‘Pattern occurs with shift ’，i-m）;

　　end;

　　end;

　　KMP算法中jump数组的构建可以通过归纳法来解决，首先确定jump［1］=0；假设jump［j］=k，也就是P［0， k］ == P［j-k， k］，如果P［j+1］ == P［k+1］，那么得出［0，k+1］ = P［j-k， j+1］，从而更加定义得出jump［j+1］ = k+1；

　　如果P［j+1］ ！= P［k+1］，那就接着比较P［j+1］ ？= P［k1+1］，其中（jump［k］ = k1），根据（jump［k］=k1）的定义，P［0，k1］ == P［k-k1， k］，根据（jump［j］=k）的定义，P［0， k］ == P［j-k， k］，根据这两个等式，推出P［0， k1］ == P［j-k1， j］，如果此时P［j+1］ == P［k1+1］，则得出：jump［j+1］ = K1 +1 = jump［k］ +1。

　　如果P［j+1］ ！= P［K1+1］，继续递归比较P［j+1］ 和P［jump［jump［k］］+1］ …。 P［1］。

　　如果依次比较都不相等，那么jump［j+1］ = 0；写成伪代码如下，可以看出其实就是模式串自我匹配的过程。

　　jump［1］：=0;

　　j：=0;

　　for i：=2 to m do

　　begin

　　while （j》0） and （P［j+1］《》P［i］） do j：=jump［j］;

　　if P［j+1］=P［i］ then j：=j+1;

　　jump［i］：=j;

　　end;

　　考虑模式串匹配不上母串的最坏情况，前缀蛮力匹配算法的时间复杂度最差是O（n×m），最好是O（n）， 其中n为母串的长度，m为模式串的长度。KMP算法最差的时间复杂度是O（n）；最好的时间复杂度是O（n/m）。

　　BM算法

　　后缀匹配，是指模式串的比较从右到左，模式串的移动也是从左到右的匹配过程，经典的BM算法其实是对后缀蛮力匹配算法的改进。所以还是先从最简单的后缀蛮力匹配算法开始。下面直接给出伪代码，注意这一行代码：j++；BM算法所做的唯一的事情就是改进了这行代码，即模式串不是每次移动一步，而是根据已经匹配的后缀信息，从而移动更多的距离。

　　j =0；

　　while （j 《= strlen（T） - strlen（P）） {

　　for （i = strlen（P） -1; i 》=0 && P［i］ ==T［i + j］; --i）

　　if （i 《0）

　　match；

　　else

　　++j；

　　}

　　为了实现更快移动模式串，BM算法定义了两个规则，好后缀规则和坏字符规则，如下图可以清晰的看出他们的含义。利用好后缀和坏字符可以大大加快模式串的移动距离，不是简单的++j，而是j+=max （shift（好后缀）， shift（坏字符））

　　

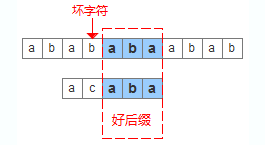
　　先来看如何根据坏字符来移动模式串，shift（坏字符）分为两种情况：

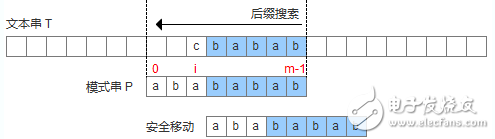
　　坏字符没出现在模式串中，这时可以把模式串移动到坏字符的下一个字符，继续比较，如下图：

　　

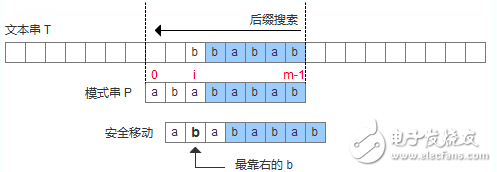
　　坏字符出现在模式串中，这时可以把模式串第一个出现的坏字符和母串的坏字符对齐，当然，这样可能造成模式串倒退移动，如下图：

　　

　　为了用代码来描述上述的两种情况，设计一个数组bmBc［‘k’］，表示坏字符‘k’在模式串中出现的位置距离模式串末尾的最大长度，那么当遇到坏字符的时候，模式串可以移动距离为： shift（坏字符） = bmBc［T［i］］-（m-1-i）。如下图：

　　

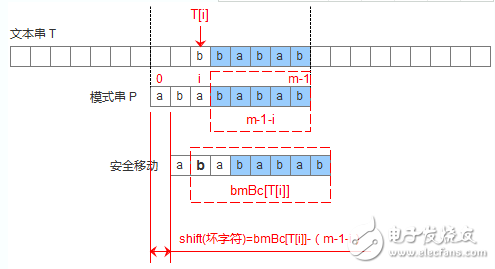
　　数组bmBc的创建非常简单，直接贴出代码如下：

　　void preBmBc（char*x， int m， int bmBc［］） {

　　int i;

　　for （i =0; i 《 ASIZE; ++i）

　　bmBc［i］ = m;

　　for （i =0; i 《 m -1; ++i）

　　bmBc［x［i］］ = m - i -1;

　　}

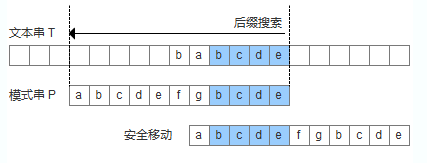
　　再来看如何根据好后缀规则移动模式串，shift（好后缀）分为三种情况：

　　模式串中有子串匹配上好后缀，此时移动模式串，让该子串和好后缀对齐即可，如果超过一个子串匹配上好后缀，则选择最靠左边的子串对齐。

　　

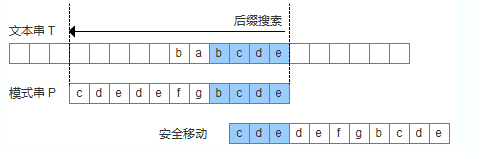
　　模式串中没有子串匹配上后后缀，此时需要寻找模式串的一个最长前缀，并让该前缀等于好后缀的后缀，寻找到该前缀后，让该前缀和好后缀对齐即可。

　　

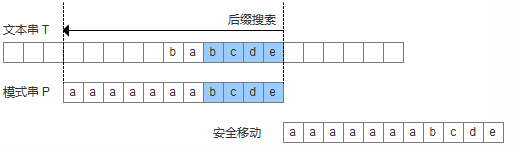
　　模式串中没有子串匹配上后后缀，并且在模式串中找不到最长前缀，让该前缀等于好后缀的后缀。此时，直接移动模式到好后缀的下一个字符。

　　

　　为了实现好后缀规则，需要定义一个数组suffix［］，其中suffix［i］ = s 表示以i为边界，与模式串后缀匹配的最大长度，如下图所示，用公式可以描述：满足P［i-s， i］ == P［m-s， m］的最大长度s。

　　

　　构建suffix数组的代码如下：

　　suffix［m-1］=m;

　　for （i=m-2；i》=0；--i）{

　　q=i;

　　while（q》=0&&P［q］==P［m-1-i+q］）

　　--q;

　　suffix［i］=i-q;

　　}

　　有了suffix数组，就可以定义bmGs［］数组，bmGs［i］ 表示遇到好后缀时，模式串应该移动的距离，其中i表示好后缀前面一个字符的位置（也就是坏字符的位置），构建bmGs数组分为三种情况，分别对应上述的移动模式串的三种情况

　　模式串中有子串匹配上好后缀

　　

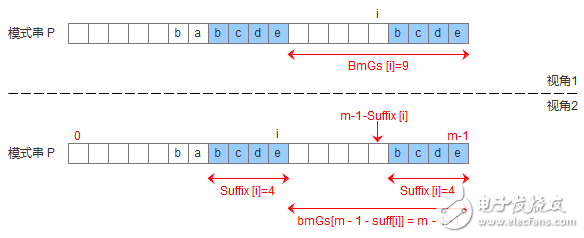
　　模式串中没有子串匹配上好后缀，但找到一个最大前缀

　

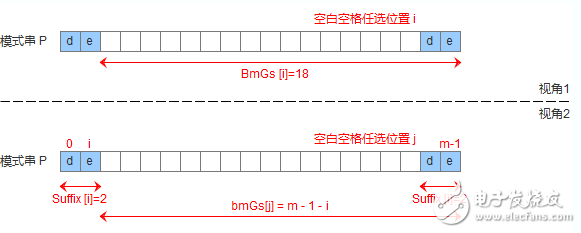
　　模式串中没有子串匹配上好后缀，但找不到一个最大前缀

　　

　　构建bmGs数组的代码如下：

　　void preBmGs（char*x， int m， int bmGs［］） {

　　int i， j， suff［XSIZE］;

　　suffixes（x， m， suff）;

　　for （i =0; i 《 m; ++i）

　　bmGs［i］ = m;

　　j =0;

　　for （i = m -1; i 》=0; --i）

　　if （suff［i］ == i +1）

　　for （; j 《 m -1- i; ++j）

　　if （bmGs［j］ == m）

　　bmGs［j］ = m -1- i;

　　for （i =0; i 《= m -2; ++i）

　　bmGs［m -1- suff［i］］ = m -1- i;

　　}

　　再来重写一遍BM算法：

　　j=0；

　　while （j 《= strlen（T） - strlen（P）） {

　　for （i = strlen（P） -1; i 》=0&& P［i］ ==T［i + j］; --i）

　　if （i 《0）

　　match；

　　else

　　j += max（bmGs［i］， bmBc［T［i］］-（m-1-i））；

　　}

　　考虑模式串匹配不上母串的最坏情况，后缀蛮力匹配算法的时间复杂度最差是O（n×m），最好是O（n），其中n为母串的长度，m为模式串的长度。