初学者必读：卷积神经网络指南（一）

摘要： 何为卷积神经网络，它来自何方？又要走向何处？跟着作者的节奏，一起来开始探索CNN吧。

卷积神经网络听起来像一个奇怪的生物学和数学的组合，但它是计算机视觉领域最具影响力的创新之一。2012年是卷积神经网络最流行的一年，因为Alex Krizhevsky用它赢得当年的ImageNet竞争（基本上算得上是计算机视觉的年度奥运），它将分类错误记录从26％降至15％，这是惊人的改善。从那时起，深度学习开始流行起来，Facebook使用神经网络进行自动标记算法，Google进行照片搜索，亚马逊的产品推荐，家庭饲料个性化的Pinterest，以及以搜索为基础设施的Instagram。

 

今天我们来看看在图像处理中如何使用CNN进行图像分类。

1.空间问题

图像分类是输入图像并输出类（猫，狗等）的任务，或是最能描述图像的类的概率。对于人类来说，这个任务是我们从出生的那一刻开始学习的第一个技能之一。我们人类能够快速，无缝地识别我们所处的环境以及我们周围的对象。当我们看到一个图像，甚至只是看着我们周围的世界，大多数时候，我们能够立即刻画场景，并给每个对象一个标签，所有这些都没有意识到注意。能够快速识别模式的这些技能，从先前的知识推测出来，适应不同的图像环境是我们的特长。我个人觉得这是人类三维视角的独特的优势，相较于机器的二维视角。

 

2.输入和输出

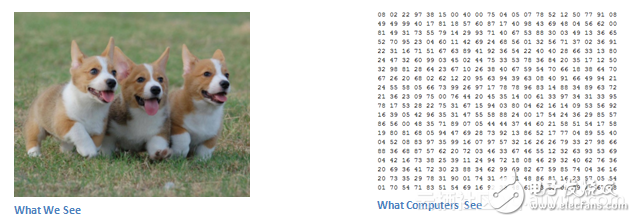
当计算机看到图像（将图像作为输入）时，它将看到的是像素值的数组。根据图像的分辨率和大小，它会看到一个32 x 32 x 3的数组（3是RGB值）。我们假设我们有一个JPG形式的彩色图像，其大小是480 x 480.代表性的数组将是480 x 480 x 3。这些数字中的每一个都给出一个从0到255的值，它描述某个点的像素强度。这些数字在我们进行图像分类时对我们毫无意义，但它是计算机可用的唯一输入。所以，这在人类的潜意识中是非常困难的。

3.我们想要电脑做什么

现在我们知道了问题以及如何输入和输出，让我们考虑一下如何解决这个问题。我们希望电脑能够区分所有的图像，并找出识别狗或识别猫的独特功能。当我们看一只狗的照片时，如果图片具有可识别的特征，例如爪子或四条腿，我们可以对其进行分类。以类似的方式，计算机能够通过寻找诸如边缘和曲线的低级特征，然后通过一系列卷积层来构建更抽象的概念来执行图像分类。这是CNN功能的总体概述，我们来详细了解一下。

3.1生物连接
首先你要有一点生物学背景。当你第一次听到“卷积神经网络”一词的时候，你可能会想到与神经科学或生物学有关的东西。CNN确实从生物学中的视觉皮质获得启发，视觉皮层是具有对视野的特定区域敏感的细胞区域，而且特定区域一般很小。这个想法在1962年由Hubel和Wiesel的实验产生的。Hubel和Wiesel发现，所有这些神经元都被组织在一个柱状结构中，并且它们一起能够产生视觉感知。具有特定任务（视觉皮层中的神经元细胞寻找特定特征）的系统内的专门组件的想法也是机器使用的构思。也是我们常说的局部感受野：就是输出图像某个节点的响应所对应的最初的输入图像的区域。这也是CNN的基础。

4.结构体

接下来我们谈谈具体细节。对CNN做什么的更详细的概述将是：拍摄图像、通过一系列卷积、非线性、池（下采样）和完全连接的层，并获得输出。如我们前面所说，输出可以是单个类或最能描述图像的类的概率。现在，困难的部分是理解这些层中的每一个，首先让我们进入最重要的一个。

4.1第一层：数学 （Math）
CNN中的第一层总是卷积层。第一件事是要确保你记得是这个转换的输入，像我们之前提到的，输入是一个32 x 32 x 3的像素数组。解释转换层的最好方法是想象一下闪光在图像左上方的手电筒，这个手电筒的光线覆盖着5×5的区域。而现在，我们可以想象这个手电筒可以滑过输入图像的所有区域。在机器学习术语中，这种手电筒被称为滤波器（或有时称为神经元或内核），并且其闪烁的区域称为接收场。现在这个过滤器也是数字数组（数字称为权重或参数）。一个非常重要的注意事项是，该滤波器的深度必须与输入深度相同（这样才可以确保数学运算），因此滤波器的尺寸为5 x 5 x 3。

译者注：滤波器：filter（带着一组固定权重的神经元）对局部输入数据进行卷积计算。

现在，我们来看看滤波器的第一个位置。当滤波器在输入图像周围滑动或卷积时，它将滤波器中的值与图像的原始像素值（AKA运算单元乘法）相乘。所以你将等到一个数字，请记住，这个数字只是代表滤波器位于图像左上方的代表。现在，我们对每个位置重复此过程。（下一步是将滤镜向右移动1个单位，然后再次向右移动1个，依此类推。）每个位置都会产生一个数字，滤波器将所有位置的滑动后，你会发现剩下的是28 x 28 x 1的数字数组，我们称之为激活图或特征图。你得到一个28 x 28阵列的原因是，有784个不同的位置，一个5 x 5的过滤器可以适应32 x 32的输入图像。这些784个数字被映射到一个28×28阵列。

 

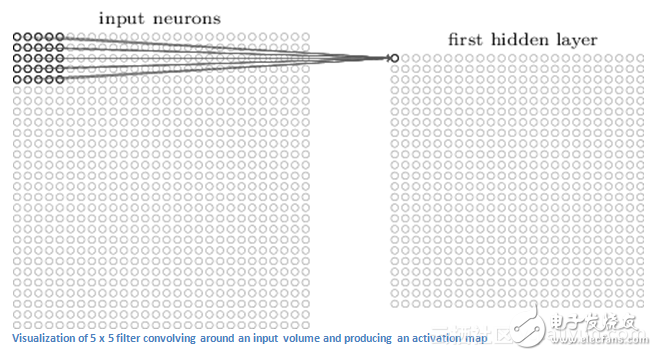
现在我们使用两个5 x 5 x 3的过滤器，而不是一个。那么我们的输出将是28 x 28 x 2.通过使用更多的滤镜，我们可以更好地保留空间维度。

4.2高层次视角（high-level perspective）

我们来谈一谈从高层次视角看这个卷积实际在做什么。这些滤波器中的每一个都可以被认为是特征标识符。当我说特征时，我指的是直边、简单的颜色和曲线。假设我们第一个滤波器为7 x 7 x 3，将成为一个曲线检测器。（在本节中，我们忽略了滤波器为3单位深的事实，为了简单起见，仅考虑滤波器和图像的顶层深度）。作为曲线检测器，滤波器将具有像素结构，其中存在的是沿着曲线形状的区域的更高的数值（记住，我们正在谈论的这些过滤器只是数字！）。

 

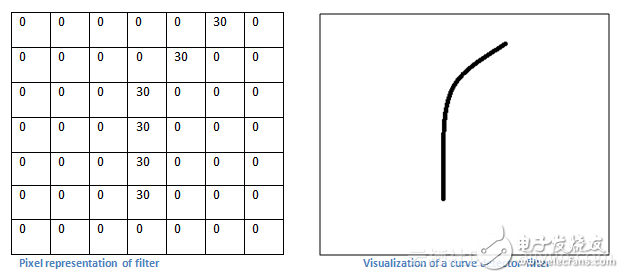
现在，让我们回想一下数学上的可视化。当我们在输入的左上角有这个过滤器时，它是该区域中滤波器和像素值之间的计算乘法。现在，让我们举一个我们要分类的图像的例子，让我们把过滤器放在左上角。

 

记住：我们要做的是将滤波器中的值与图像的原始像素值相乘。

 

在输入图像中，如果存在类似于该滤波器表示的曲线的形状，则所有乘法相加在一起将导致较大的值！现在我们来看看当我们移动过滤器时会发生什么。

 

值要低得多！这是因为图像部分中没有任何响应曲线滤波器中的内容。请记住，此转换图层的输出是激活图。因此，在一个滤波器卷积的简单情况下（如果该滤波器是曲线检测器），那么激活图将显示图像中最可能出现曲线的区域。在这个例子中，我们的28 x 28 x 1激活图的左上角值将为6600。我们的激活图中右上角的值将为0，因为输入中没有任何内容导致过滤器被激活（或者更简单地说，原始图像的该区域中没有曲线）。记住，这只是一个滤波器。它用于检测向外和向右弯曲的线条。我们也可以使用其他滤波器，用于向左或直边弯曲的线条。

 

4.3深入网络
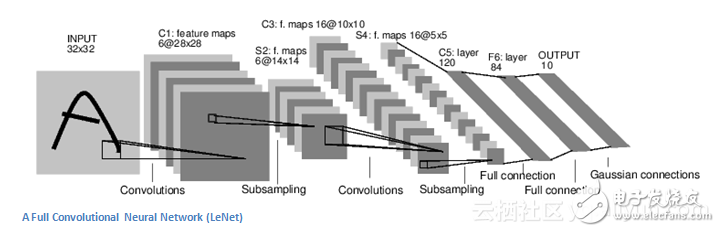
在传统的卷积神经网络架构中，其他层次之间非常分明。我强烈地建议有兴趣的人阅读并理解他们的功能和效果，但总体来说，它们提供了非线性的维度，有助于提高网络的鲁棒性和控制过度。经典的CNN架构如下所示：

然而，最后一层是非常重要的，我稍后会介绍。让我们回顾一下我们刚刚所学到的东西。

我们讨论了第一个转换层中的滤波器被设计为检测什么。它们检测低级特征，如边缘和曲线。可以想象，为了预测图像是否是一种对象，我们需要网络能够识别更高级别的特征，例如手或爪子或耳朵。所以让我们考虑第一个转换层之后的网络输出。当我们通过另一个转换层时，第一个转换层的输出成为第二个转换层的输入。

当我们谈论第一层时，输入只是原始图像。然而，当我们谈论第二个转换层时，输入是从第一层产生的激活图。因此，输入的每一层基本上都描述了原始图像中出现某些低级特征的位置。现在当你应用一组滤波器（通过第二个转换层）时，输出将是表示较高级特征的激活图。这些特征的类型可以是半圆（曲线和直边的组合）或正方形（几条直边的组合）。当你通过网络并通过更多的转换层时，你将获得代表越来越复杂特征的激活图。

4.4完全连接层
现在我们可以检测到这些高级特征，接下来就是一个完全连接的层。该层基本上接收一个输入卷（volume）（无论是在其前面的conv或ReLU或池层的输出），并输出N维向量，其中N是程序必须选择的类的数量。例如，如果你想要一个数字分类程序，N将是10，因为有10位数字。该N维向量中的每个数字表示某一类的概率。例如，如果用于数字分类程序的结果向量是[0，1，1，75，0，0 ，0，0，0，05]，则这表示图像为1的概率为10％，10％的概率为图像是2，图像为3的概率为75％，图像为9的概率为5％。（注：还有其他方式可以表示输出，但我只是显示softmax方法。）

这个完全连接层可以查看上一层的输出（表示高级特征的激活图），并确定与特定类最相关的特征。例如，如果程序预测某些图像是狗，则在激活图中将具有高值，这些图表示诸如爪或四条腿等高级特征。类似地，如果程序预测某些图像是鸟，它将具有高值的激活图，代表高级特征，如翅膀或喙等。完全连接层最后输出的是一个概率。

 

4.5训练
这是我有意没有提到的神经网络的另一个方面，它可能是最重要的部分。第一个转换层中的滤波器如何查找边和曲线？完全连接层如何看激活图？每个层中的滤波器如何知道这是什么值？计算机能够调整其滤波器值（或权重）的方式是通过称为反向传播的训练过程。

在进行反向传播之前，我们必须先退后一步，谈一谈神经网络为了工作需要什么。现在我们都出生了，我们不知道什么是猫或狗或鸟。以类似的方式，在CNN启动之前，权重或滤波器值被随机化。过滤器不知道如何寻找边缘和曲线。然而，随着年龄的增长，我们的父母和老师向我们展示了不同的图片，并给了我们相应的标签。给予图像和标签其实就是CNN的训练过程。我们有一个训练集，有成千上万的狗，猫和鸟的图像，而且每个图像都有一个标签。

回到backprop（反向传播）

反向传播可以分为四个不同的部分：正向传递，损失函数，后向传递和权重更新。在我们的第一个训练中，由于所有权重或滤波器值都被随机初始化，所以输出可能会像[.1 .1 .1 .1 .1 .1 .1 .1 .1]。具有当前权重的网络不能寻找那些低级特征，因此不能对分类有什么合理的结论。记住，我们现在正在使用的是训练数据，该数据同时具有图像和标签。例如，输入的第一个训练图像为3，图像的标签为[0 0 0 1 0 0 0 0 0 0]。损失函数可以以许多不同的方式定义，但常见的是MSE（均方误差），它是½倍（实际预测）平方。

现在，我们想要达到预测标签（ConvNet的输出）与训练标签相同的点（这意味着我们的网络获得了预测能力）。为了达到目的，我们要尽量减少损失量。将其视为微积分中的优化问题，我们希望了解哪些输入直接地导致了网络的丢失。

 

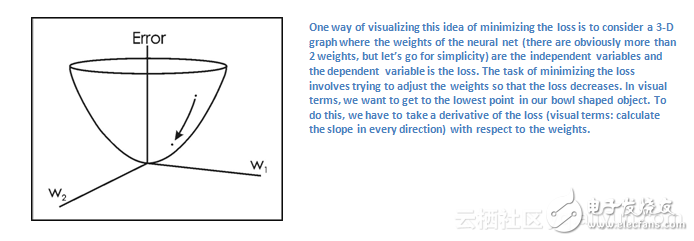
现在，我们想要做的是执行一个向后传递的网络，这是决定哪些权重有助于损失，并找到调整方式，以使损失减少。这是权重更新。这时我们把所有权重和更新，以便它们沿梯度的相反方向改变。

 

向前传递>损失函数>向后传递>参数更新是一个训练迭代。该程序将对每组训练图像（通常称为批次）重复此过程以进行固定次数的迭代。一旦完成了最后一个训练示例的参数更新，网络应该被训练得很好，以保证层的权重得到调整。

4.6测试
最后，要看我们的CNN是否有效，我们有一套不同的图像和标签，并通过CNN传递图像。我们将输出与地面事实进行比较，看看我们的网络是否正常工作！

5.总结：

虽然这篇文章应该是了解CNN的一个好的开始，但绝不是全面的概述。这篇文章中没有讨论包括非线性和汇集层以及网络的超参数，如滤波器大小，步幅和填充。还没有讨论如网络架构，批量归一化，梯度消失，dropout，初始化，非凸优化，偏差，损失函数的选择，数据增加，正则化方法，反向传播的修改等问题。如果你想要了解这些，请继续关注我！