

卷积神经网络检测脸部关键点的教程之两个重要参数:学习率,学习动量
人工智能
描述
上个模型令人讨厌的地方是光训练就花了一个小时的时间,等结果并不是一个令人心情愉快的事情。这一部分,我们将讨论将两个技巧结合让网络训练的更快!
直觉上的解决办法是,开始训练时取一个较高的学习率,随着迭代次数的增多不停的减小这个值。这是有道理的,因为开始的时候我们距离全局最优点非常远,我们想要朝着最优点的方向大步前进;然而里最优点越近,我们就前进的越谨慎,以免一步跨过去。举个例子说就是你乘火车回家,但你进家门的时候肯定是走进去,不能让火车开进去。
关于深度学习中的初始化和动量的重要性是Ilya Sutskever等人的谈话和论文的标题。在那里,我们学习了另一个有用的技巧来促进深度学习:即在训练期间增加优化方法的动量参数。
在我们以前的模型中,我们将学习率和学习势初始化为静态的0.01和0.9。让我们来改变这两个参数,使得学习率随着迭代次数线性减小,同时让学习动量增大。
NeuralNet允许我们在训练时通过on_epoch_finished函数来更新参数。于是我们传一个函数给on_epoch_finished,使得这个函数在每次迭代之后被调用。然而,在我们改变学习率和学习势这两个参数之前,我们必须将这两个参数改变为Theano shared variables。好在这非常简单。
import theano
def float32(k):
return np.cast['float32'](k)
net4 = NeuralNet(
# ...
update_learning_rate=theano.shared(float32(0.03)),
update_momentum=theano.shared(float32(0.9)),
# ...
)
我们传递的回调函数或者回调列表在调用时需要两个参数:nn,它是NeuralNet的实例;train_history,它和nn.history是同一个值。
不使用硬编码值的毁掉函数,我们将使用一个可参数化的类,在其中定义一个call函数来作为我们的回调函数。让我们把这个类叫做AdjustVariable,实现是相当简单的:
class AdjustVariable(object):
def __init__(self, name, start=0.03, stop=0.001):
self.name = name
self.start, self.stop = start, stop
self.ls = None
def __call__(self, nn, train_history):
if self.ls is None:
self.ls = np.linspace(self.start, self.stop, nn.max_epochs)
epoch = train_history[-1]['epoch']
new_value = float32(self.ls[epoch - 1])
getattr(nn, self.name).set_value(new_value)
现在让我们把这些变化放到一起,并开始准备训练网络:
net4 = NeuralNet(
# ...
update_learning_rate=theano.shared(float32(0.03)),
update_momentum=theano.shared(float32(0.9)),
# ...
regression=True,
# batch_iterator_train=FlipBatchIterator(batch_size=128),
on_epoch_finished=[
AdjustVariable('update_learning_rate', start=0.03, stop=0.0001),
AdjustVariable('update_momentum', start=0.9, stop=0.999),
],
max_epochs=3000,
verbose=1,
)
X, y = load2d()
net4.fit(X, y)
with open('net4.pickle', 'wb') as f:
pickle.dump(net4, f, -1)
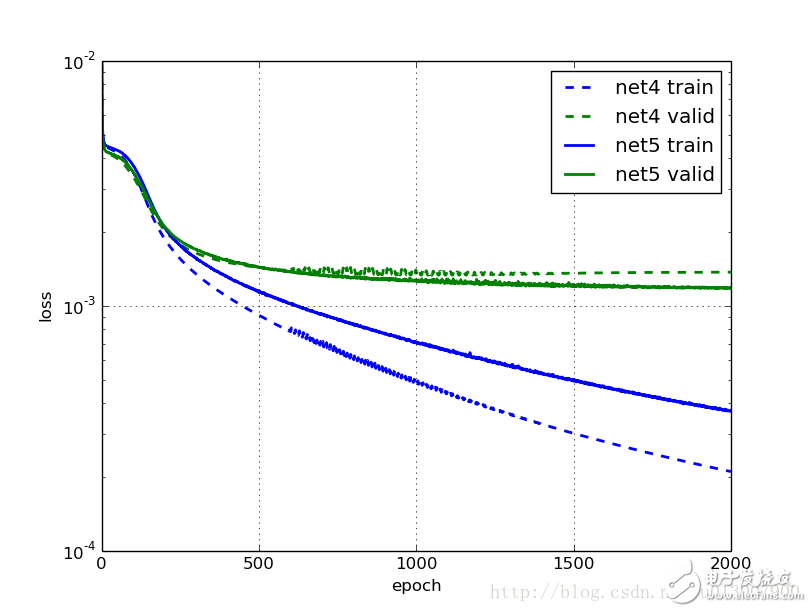
我们将训练两个网络:net4不使用我们的FlipBatchIterator,net5采用了。 除此之外,他们是相同的。
这是net4的学习:
Epoch | Train loss | Valid loss | Train / Val
--------|--------------|--------------|----------------
50 | 0.004216 | 0.003996 | 1.055011
100 | 0.003533 | 0.003382 | 1.044791
250 | 0.001557 | 0.001781 | 0.874249
500 | 0.000915 | 0.001433 | 0.638702
750 | 0.000653 | 0.001355 | 0.481806
1000 | 0.000496 | 0.001387 | 0.357917
酷,训练发生得更快了! 在我们调整学习速度和学习动量之前,在500代和1000代的训练误差是以前在net2中的一半。 这一次,泛化程度似乎已经在750个左右的时期之后停止改善; 看起来没有什么意义的培训更长。
net5用了数据扩充之后怎么样?
poch | Train loss | Valid loss | Train / Val
--------|--------------|--------------|----------------
50 | 0.004317 | 0.004081 | 1.057609
100 | 0.003756 | 0.003535 | 1.062619
250 | 0.001765 | 0.001845 | 0.956560
500 | 0.001135 | 0.001437 | 0.790225
750 | 0.000878 | 0.001313 | 0.668903
1000 | 0.000705 | 0.001260 | 0.559591
1500 | 0.000492 | 0.001199 | 0.410526
2000 | 0.000373 | 0.001184 | 0.315353
再次,我们有比net3更快的训练,更好的结果。在1000次迭代之后,结果比net3迭代了3000次的效果还要好。 此外,使用数据扩充训练的模型现在比没有数据扩充的模型好约10%。
丢弃技巧(Dropout)
2012年,在通过防止特征探测器的共适应来改进神经网络论文中引入了dropout,它是一种流行的正则化技术,工作非常好。我不会深入了解它为什么这么好的细节,你可以在别的地方读到。
像任何其他正则化技术一样,如果我们有一个过度拟合的网络,dropout才有意义,这在上一节中我们训练的net5网络显然是这样。 重要的是要记住,让你的网络训练得很好,首先过拟合,然后正则化。
要在Lasagne中使用dropout,我们将在现有图层之间添加DropoutLayer图层,并为每个图层指定退出概率。 这里是我们新网的完整定义。我在这些行的末尾添加了一个#!,用于区分和net5的不同。
net6 = NeuralNet(
layers=[
('input', layers.InputLayer),
('conv1', layers.Conv2DLayer),
('pool1', layers.MaxPool2DLayer),
('dropout1', layers.DropoutLayer), # !
('conv2', layers.Conv2DLayer),
('pool2', layers.MaxPool2DLayer),
('dropout2', layers.DropoutLayer), # !
('conv3', layers.Conv2DLayer),
('pool3', layers.MaxPool2DLayer),
('dropout3', layers.DropoutLayer), # !
('hidden4', layers.DenseLayer),
('dropout4', layers.DropoutLayer), # !
('hidden5', layers.DenseLayer),
('output', layers.DenseLayer),
],
input_shape=(None, 1, 96, 96),
conv1_num_filters=32, conv1_filter_size=(3, 3), pool1_pool_size=(2, 2),
dropout1_p=0.1, # !
conv2_num_filters=64, conv2_filter_size=(2, 2), pool2_pool_size=(2, 2),
dropout2_p=0.2, # !
conv3_num_filters=128, conv3_filter_size=(2, 2), pool3_pool_size=(2, 2),
dropout3_p=0.3, # !
hidden4_num_units=500,
dropout4_p=0.5, # !
hidden5_num_units=500,
output_num_units=30, output_nonlinearity=None,
update_learning_rate=theano.shared(float32(0.03)),
update_momentum=theano.shared(float32(0.9)),
regression=True,
batch_iterator_train=FlipBatchIterator(batch_size=128),
on_epoch_finished=[
AdjustVariable('update_learning_rate', start=0.03, stop=0.0001),
AdjustVariable('update_momentum', start=0.9, stop=0.999),
],
max_epochs=3000,
verbose=1,
)
我们的网路现在已经大到可以让Python报一个“超过最大递归限制”错误了,所以为了避免这一点,我们最好增加python的递归限制。
import sys
sys.setrecursionlimit(10000)
X, y = load2d()
net6.fit(X, y)
import cPickle as pickle
with open('net6.pickle', 'wb') as f:
pickle.dump(net6, f, -1)
看一下我们现在的训练,我们注意到训练速度又变慢了,以为添加了dropout,这是不出意料的效果。然而,整个网络的表现事实上超过了net5:
Epoch | Train loss | Valid loss | Train / Val
--------|--------------|--------------|---------------
50 | 0.004619 | 0.005198 | 0.888566
100 | 0.004369 | 0.004182 | 1.044874
250 | 0.003821 | 0.003577 | 1.068229
500 | 0.002598 | 0.002236 | 1.161854
1000 | 0.001902 | 0.001607 | 1.183391
1500 | 0.001660 | 0.001383 | 1.200238
2000 | 0.001496 | 0.001262 | 1.185684
2500 | 0.001383 | 0.001181 | 1.171006
3000 | 0.001306 | 0.001121 | 1.164100
过拟合也似乎没有那么糟糕。虽然我们必须小心这些数字:训练错误和验证错误之间的比率现在有一个稍微不同的意义,因为训练错误评估与遗漏,而验证错误评估没有遗漏。训练错误的更有价值的值是
from sklearn.metrics import mean_squared_error
print mean_squared_error(net6.predict(X), y)
# prints something like 0.0010073791
在我们以前的没有dropout的模型中,训练上的误差为0.000373。 所以不仅我们的dropout网表现略微好一点,它的过拟合也比我们以前的模型少得多。 这是个好消息,因为这意味着当我们使网络更大(更具表现力)时,我们可以期望更好的性能。 这就是我们将尝试下一步:我们将最后两个隐藏层中的单位数从500增加到1000。我们需要修改这些行:
net7 = NeuralNet(
# ...
hidden4_num_units=1000, # !
dropout4_p=0.5,
hidden5_num_units=1000, # !
# ...
)
相比于没有dropout的网络,改进效果更加明显:
Epoch | Train loss | Valid loss | Train / Val
--------|--------------|--------------|---------------
50 | 0.004756 | 0.007043 | 0.675330
100 | 0.004440 | 0.005321 | 0.834432
250 | 0.003974 | 0.003928 | 1.011598
500 | 0.002574 | 0.002347 | 1.096366
1000 | 0.001861 | 0.001613 | 1.153796
1500 | 0.001558 | 0.001372 | 1.135849
2000 | 0.001409 | 0.001230 | 1.144821
2500 | 0.001295 | 0.001146 | 1.130188
3000 | 0.001195 | 0.001087 | 1.099271
有一点过拟合,但效果着实不错。我的感觉是,如果继续增加训练次数,模型效果会变得更棒。试一下:
net12 = NeuralNet(
# ...
max_epochs=10000,
# ...
)
Epoch | Train loss | Valid loss | Train / Val
--------|--------------|--------------|---------------
50 | 0.004756 | 0.007027 | 0.676810
100 | 0.004439 | 0.005321 | 0.834323
500 | 0.002576 | 0.002346 | 1.097795
1000 | 0.001863 | 0.001614 | 1.154038
2000 | 0.001406 | 0.001233 | 1.140188
3000 | 0.001184 | 0.001074 | 1.102168
4000 | 0.001068 | 0.000983 | 1.086193
5000 | 0.000981 | 0.000920 | 1.066288
6000 | 0.000904 | 0.000884 | 1.021837
7000 | 0.000851 | 0.000849 | 1.002314
8000 | 0.000810 | 0.000821 | 0.985769
9000 | 0.000769 | 0.000803 | 0.957842
10000 | 0.000760 | 0.000787 | 0.966583
现在你是dropout魔力的见证者了。:-)
让我们比较一下到目前为止我们训练过的网络:
Name Description Epochs Train loss Valid loss
net1 single hidden 400 0.002244 0.003255
net2 convolutions 1000 0.001079 0.001566
net3 augmentation 3000 0.000678 0.001288
net4 mom + lr adj 1000 0.000496 0.001387
net5 net4 + augment 2000 0.000373 0.001184
net6 net5 + dropout 3000 0.001306 0.001121
net7 net6 + epochs 10000 0.000760 0.000787
-
如何优化BP神经网络的学习率2025-02-12 1468
-
卷积神经网络的基本结构及其功能2024-07-02 4471
-
详解深度学习、神经网络与卷积神经网络的应用2024-01-11 3438
-
卷积神经网络层级结构 卷积神经网络的卷积层讲解2023-08-21 10428
-
卷积神经网络原理:卷积神经网络模型和卷积神经网络算法2023-08-17 2151
-
卷积神经网络简介:什么是机器学习?2023-02-23 25347
-
卷积神经网络模型发展及应用2022-08-02 13202
-
可分离卷积神经网络在 Cortex-M 处理器上实现关键词识别2021-07-26 3704
-
解析深度学习:卷积神经网络原理与视觉实践2020-06-14 3427
-
卷积神经网络—深度卷积网络:实例探究及学习总结2020-05-22 3433
-
卷积神经网络的主要两个特征2020-05-04 14055
-
卷积神经网络检测脸部关键点的教程之卷积神经网络训练与数据扩充2017-11-16 3773
-
用卷积神经网络检测脸部关键点的教程(一)2017-02-13 3090
全部0条评论

快来发表一下你的评论吧 !

