利用Cordic算法来计算三角函数的值

三角函数的计算是个复杂的主题，有计算机之前，人们通常通过查找三角函数表来计算任意角度的三角函数的值。这种表格在人们刚刚产生三角函数的概念的时候就已经有了，它们通常是通过从已知值（比如sin(π/2)=1）开始并重复应用半角和和差公式而生成。

现在有了计算机，三角函数表便推出了历史的舞台。但是像我这样的喜欢刨根问底的人，不禁要问计算机又是如何计算三角函数值的呢。最容易想到的办法就是利用级数展开，比如泰勒级数来逼近三角函数，只要项数取得足够多就能以任意的精度来逼近函数值。除了泰勒级数逼近之外，还有其他许多的逼近方法，比如切比雪夫逼近、最佳一致逼近和Padé逼近等。

所有这些逼近方法本质上都是用多项式函数来近似我们要计算的三角函数，计算过程中必然要涉及到大量的浮点运算。在缺乏硬件乘法器的简单设备上（比如没有浮点运算单元的单片机），用这些方法来计算三角函数会非常的费时。为了解决这个问题，J. Volder于1959年提出了一种快速算法，称之为CORDIC(COordinate Rotation DIgital Computer) 算法，这个算法只利用移位和加减运算，就能计算常用三角函数值，如Sin，Cos，Sinh，Cosh等函数。 J. Walther在1974年在这种算法的基础上进一步改进，使其可以计算出多种超越函数，更大的扩展了Cordic 算法的应用。因为Cordic 算法只用了移位和加法，很容易用纯硬件来实现，因此我们常能在FPGA运算平台上见到它的身影。不过，大多数的软件程序员们都没有听说过这种算法，也更不会主动的去用这种算法。其实，在嵌入式软件开发，尤其是在没有浮点运算指令的嵌入式平台（比如定点型DSP）上做开发时，还是会遇上可以用到Cordic 算法的情况的，所以掌握基本的Cordic算法还是有用的。

从二分查找法说起
先从一个例子说起，知道平面上一点在直角坐标系下的坐标（X,Y）=（100，200），如何求的在极坐标系下的坐标（ρ,θ）。用计算器计算一下可知答案是（223.61，63.435）。

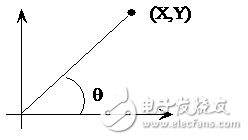
图 1 直角坐标系到极坐标系的转换

 

可能有读者会问，计算中用到了 sin 函数和 cos 函数，这些值又是怎么计算呢。很简单，我们只用到很少的几个特殊点的sin 函数和 cos 函数的值，提前计算好存起来，用时查表。

下面给出上面方法的C 语言实现。
       
#include
#include 

double my_atan2(double x, double y);
int main(void)
{
double z = my_atan2(100.0, 200.0);
printf("\n z = %f \n", z);

return 0;
}

double my_atan2(double x, double y)
{
const double sine[] = {0.7071067811865,0.3826834323651,0.1950903220161,0.09801714032956,
0.04906767432742,0.02454122852291,0.01227153828572,0.006135884649154,0.003067956762966
,0.001533980186285,7.669903187427045e-4,3.834951875713956e-4,1.917475973107033e-4,
9.587379909597735e-5,4.793689960306688e-5,2.396844980841822e-5
};

const double cosine[] = {0.7071067811865,0.9238795325113,0.9807852804032,0.9951847266722,
0.9987954562052,0.9996988186962,0.9999247018391,0.9999811752826,0.9999952938096,
0.9999988234517,0.9999997058629,0.9999999264657,0.9999999816164,0.9999999954041,
0.999999998851,0.9999999997128
};

int i = 0;
double x_new, y_new;
double angleSum = 0.0;
double angle = 45.0;

for(i = 0; i < 15; i++)
{
if(y > 0)
{
x_new = x * cosine[i] + y * sine[i];
y_new = y * cosine[i] - x * sine[i];
x = x_new;
y = y_new;
angleSum += angle;
}
else
{
x_new = x * cosine[i] - y * sine[i];
y_new = y * cosine[i] + x * sine[i];
x = x_new;
y = y_new;
angleSum -= angle;
}
printf("Debug: i = %d angleSum = %f, angle = %f\n", i, angleSum, angle);
angle /= 2;
}
return angleSum;
}

程序运行的输出结果如下：
Debug: i = 0 angleSum = 45.000000, angle = 45.000000
Debug: i = 1 angleSum = 67.500000, angle = 22.500000
Debug: i = 2 angleSum = 56.250000, angle = 11.250000
Debug: i = 3 angleSum = 61.875000, angle = 5.625000
Debug: i = 4 angleSum = 64.687500, angle = 2.812500
Debug: i = 5 angleSum = 63.281250, angle = 1.406250
Debug: i = 6 angleSum = 63.984375, angle = 0.703125
Debug: i = 7 angleSum = 63.632813, angle = 0.351563
Debug: i = 8 angleSum = 63.457031, angle = 0.175781
Debug: i = 9 angleSum = 63.369141, angle = 0.087891
Debug: i = 10 angleSum = 63.413086, angle = 0.043945
Debug: i = 11 angleSum = 63.435059, angle = 0.021973
Debug: i = 12 angleSum = 63.424072, angle = 0.010986
Debug: i = 13 angleSum = 63.429565, angle = 0.005493
Debug: i = 14 angleSum = 63.432312, angle = 0.002747

z = 63.432312

减少乘法运算
现在已经有点 Cordic 算法的样子了，但是我们看到没次循环都要计算 4 次浮点数的乘法运算，运算量还是太大了。还需要进一步的改进。改进的切入点当然还是坐标变换的过程。我们将坐标变换公式变一下形。

 

可以看出 cos(θ)可以从矩阵运算中提出来。我们可以做的再彻底些，直接把 cos(θ) 给省略掉。

省略cos(θ)后发生了什么呢，每次旋转后的新坐标点到原点的距离都变长了，放缩的系数是1/cos(θ)。不过没有关系，我们求的是θ，不关心ρ的改变。这样的变形非常的简单，但是每次循环的运算量一下就从4次乘法降到了2次乘法了。

还是给出 C 语言的实现：
double my_atan3(double x, double y)
{
const double tangent[] = {1.0,0.4142135623731,0.1989123673797,0.09849140335716,0.04912684976947,
0.02454862210893,0.01227246237957,0.006136000157623,0.003067971201423,
0.001533981991089,7.669905443430926e-4,3.83495215771441e-4,1.917476008357089e-4,
9.587379953660303e-5,4.79368996581451e-5,2.3968449815303e-5
};

int i = 0;
double x_new, y_new;
double angleSum = 0.0;
double angle = 45.0;

for(i = 0; i < 15; i++)
{
if(y > 0)
{
x_new = x + y * tangent[i];
y_new = y - x * tangent[i];
x = x_new;
y = y_new;
angleSum += angle;
}
else
{
x_new = x - y * tangent[i];
y_new = y + x * tangent[i];
x = x_new;
y = y_new;
angleSum -= angle;
}
printf("Debug: i = %d angleSum = %f, angle = %f, ρ = %f\n", i, angleSum, angle, hypot(x,y));
angle /= 2;
}
return angleSum;
}

计算的结果是：
Debug: i = 0 angleSum = 45.000000, angle = 45.000000, ρ = 316.227766
Debug: i = 1 angleSum = 67.500000, angle = 22.500000, ρ = 342.282467
Debug: i = 2 angleSum = 56.250000, angle = 11.250000, ρ = 348.988177
Debug: i = 3 angleSum = 61.875000, angle = 5.625000, ρ = 350.676782
Debug: i = 4 angleSum = 64.687500, angle = 2.812500, ρ = 351.099697
Debug: i = 5 angleSum = 63.281250, angle = 1.406250, ρ = 351.205473
Debug: i = 6 angleSum = 63.984375, angle = 0.703125, ρ = 351.231921
Debug: i = 7 angleSum = 63.632813, angle = 0.351563, ρ = 351.238533
Debug: i = 8 angleSum = 63.457031, angle = 0.175781, ρ = 351.240186
Debug: i = 9 angleSum = 63.369141, angle = 0.087891, ρ = 351.240599
Debug: i = 10 angleSum = 63.413086, angle = 0.043945, ρ = 351.240702
Debug: i = 11 angleSum = 63.435059, angle = 0.021973, ρ = 351.240728
Debug: i = 12 angleSum = 63.424072, angle = 0.010986, ρ = 351.240734
Debug: i = 13 angleSum = 63.429565, angle = 0.005493, ρ = 351.240736
Debug: i = 14 angleSum = 63.432312, angle = 0.002747, ρ = 351.240736

z = 63.432312

消除乘法运算
我们已经成功的将乘法的次数减少了一半，还有没有可能进一步降低运算量呢？还要从计算式入手。

第一次循环时，tan(45)=1，所以第一次循环实际上是不需要乘法运算的。第二次运算呢？
Tan(22.5)=0.4142135623731,很不幸，第二次循环乘数是个很不整的小数。是否能对其改造一下呢？答案是肯定的。第二次选择22.5度是因为二分查找法的查找效率最高。如果选用个在22.5到45度之间的值，查找的效率会降低一些。如果稍微降低一点查找的效率能让我们有效的减少乘法的次数，使最终的计算速度提高了，那么这种改进就是值得的。

我们发现tan(26.565051177078)=0.5，如果我们第二次旋转采用26.565051177078度，那么乘数变为0.5，如果我们采用定点数运算的话（没有浮点协处理器时为了加速计算我们会大量的采用定点数算法）乘以0.5就相当于将乘数右移一位。右移运算是很快的，这样第二次循环中的乘法运算也被消除了。

类似的方法，第三次循环中不用11.25度，而采用 14.0362434679265 度。
Tan(14.0362434679265)= 1/4

乘数右移两位就可以了。剩下的都以此类推。
tan(45)= 1
tan(26.565051177078)= 1/2
tan(14.0362434679265)= 1/4
tan(7.1250163489018)= 1/8
tan(3.57633437499735)= 1/16
tan(1.78991060824607)= 1/32
tan(0.8951737102111)= 1/64
tan(0.4476141708606)= 1/128
tan(0.2238105003685)= 1/256

还是给出C语言的实现代码，我们采用循序渐进的方法，先给出浮点数的实现（因为用到了浮点数，所以并没有减少乘法运算量，查找的效率也比二分查找法要低，理论上说这个算法实现很低效。不过这个代码的目的在于给出算法实现的示意性说明，还是有意义的）。
double my_atan4(double x, double y)
{
const double tangent[] = {1.0, 1 / 2.0, 1 / 4.0, 1 / 8.0, 1 / 16.0,
1 / 32.0, 1 / 64.0, 1 / 128.0, 1 / 256.0, 1 / 512.0,
1 / 1024.0, 1 / 2048.0, 1 / 4096.0, 1 / 8192.0, 1 / 16384.0
};
const double angle[] = {45.0, 26.565051177078, 14.0362434679265, 7.1250163489018, 3.57633437499735,
1.78991060824607, 0.8951737102111, 0.4476141708606, 0.2238105003685, 0.1119056770662,
0.0559528918938, 0.027976452617, 0.01398822714227, 0.006994113675353, 0.003497056850704
};

int i = 0;
double x_new, y_new;
double angleSum = 0.0;

for(i = 0; i < 15; i++)
{
if(y > 0)
{
x_new = x + y * tangent[i];
y_new = y - x * tangent[i];
x = x_new;
y = y_new;
angleSum += angle[i];
}
else
{
x_new = x - y * tangent[i];
y_new = y + x * tangent[i];
x = x_new;
y = y_new;
angleSum -= angle[i];
}
printf("Debug: i = %d angleSum = %f, angle = %f, ρ = %f\n", i, angleSum, angle[i], hypot(x, y));
}
return angleSum;
}

程序运行的输出结果如下：
Debug: i = 0 angleSum = 45.000000, angle = 45.000000, ρ = 316.227766
Debug: i = 1 angleSum = 71.565051, angle = 26.565051, ρ = 353.553391
Debug: i = 2 angleSum = 57.528808, angle = 14.036243, ρ = 364.434493
Debug: i = 3 angleSum = 64.653824, angle = 7.125016, ρ = 367.270602
Debug: i = 4 angleSum = 61.077490, angle = 3.576334, ρ = 367.987229
Debug: i = 5 angleSum = 62.867400, angle = 1.789911, ρ = 368.166866
Debug: i = 6 angleSum = 63.762574, angle = 0.895174, ρ = 368.211805
Debug: i = 7 angleSum = 63.314960, angle = 0.447614, ρ = 368.223042
Debug: i = 8 angleSum = 63.538770, angle = 0.223811, ρ = 368.225852
Debug: i = 9 angleSum = 63.426865, angle = 0.111906, ρ = 368.226554
Debug: i = 10 angleSum = 63.482818, angle = 0.055953, ρ = 368.226729
Debug: i = 11 angleSum = 63.454841, angle = 0.027976, ρ = 368.226773
Debug: i = 12 angleSum = 63.440853, angle = 0.013988, ρ = 368.226784
Debug: i = 13 angleSum = 63.433859, angle = 0.006994, ρ = 368.226787
Debug: i = 14 angleSum = 63.437356, angle = 0.003497, ρ = 368.226788

z = 63.437356

#p#定点数算法e#

有了上面的准备，我们可以来讨论定点数算法了。所谓定点数运算，其实就是整数运算。我们用256 表示1度。这样的话我们就可以精确到1/256=0.00390625 度了，这对于大多数的情况都是足够精确的了。256 表示1度，那么45度就是 45*256 = 115200。其他的度数以此类推。

 

序号

 

度数

 

×256

 

取整

 

1

 

45.0

 

11520

 

11520

 

2

 

26.565051177078

 

6800.65310133196

 

6801

 

3

 

14.0362434679265

 

3593.27832778918

 

3593

 

4

 

7.1250163489018

 

1824.00418531886

 

1824

 

5

 

3.57633437499735

 

915.541599999322

 

916

 

6

 

1.78991060824607

 

458.217115710994

 

458

 

7

 

0.8951737102111

 

229.164469814035

 

229

 

8

 

0.4476141708606

 

114.589227740302

 

115

 

9

 

0.2238105003685

 

57.2954880943458

 

57

 

10

 

0.1119056770662

 

28.647853328949

 

29

 

11

 

0.0559528918938

 

14.3239403248137

 

14

 

12

 

0.027976452617

 

7.16197186995294

 

7

 

13

 

0.01398822714227

 

3.58098614841984

 

4

 

14

 

0.006994113675353

 

1.79049310089035

 

2

 

15

 

0.003497056850704

 

0.8952465537802

 

1

 

 

C 代码如下：
int my_atan5(int x, int y)
{
const int angle[] = {11520, 6801, 3593, 1824, 916, 458, 229, 115, 57, 29, 14, 7, 4, 2, 1};

int i = 0;
int x_new, y_new;
int angleSum = 0;

x *= 1024;// 将 X Y 放大一些，结果会更准确
y *= 1024;

for(i = 0; i < 15; i++)
{
if(y > 0)
{
x_new = x + (y >> i);
y_new = y - (x >> i);
x = x_new;
y = y_new;
angleSum += angle[i];
}
else
{
x_new = x - (y >> i);
y_new = y + (x >> i);
x = x_new;
y = y_new;
angleSum -= angle[i];
}
printf("Debug: i = %d angleSum = %d, angle = %d\n", i, angleSum, angle[i]);
}
return angleSum;
}

计算结果如下：
Debug: i = 0 angleSum = 11520, angle = 11520
Debug: i = 1 angleSum = 18321, angle = 6801
Debug: i = 2 angleSum = 14728, angle = 3593
Debug: i = 3 angleSum = 16552, angle = 1824
Debug: i = 4 angleSum = 15636, angle = 916
Debug: i = 5 angleSum = 16094, angle = 458
Debug: i = 6 angleSum = 16323, angle = 229
Debug: i = 7 angleSum = 16208, angle = 115
Debug: i = 8 angleSum = 16265, angle = 57
Debug: i = 9 angleSum = 16236, angle = 29
Debug: i = 10 angleSum = 16250, angle = 14
Debug: i = 11 angleSum = 16243, angle = 7
Debug: i = 12 angleSum = 16239, angle = 4
Debug: i = 13 angleSum = 16237, angle = 2
Debug: i = 14 angleSum = 16238, angle = 1

z = 16238

16238/256=63.4296875度，精确的结果是63.4349499度，两个结果的差为0.00526，还是很精确的。
到这里 CORDIC 算法的最核心的思想就介绍完了。当然，这里介绍的只是CORDIC算法最基本的内容，实际上，利用CORDIC 算法不光可以计算 atan 函数，其他的像 Sin，Cos，Sinh，Cosh 等一系列的函数都可以计算，不过那些都不在本文的讨论范围内了。另外，每次旋转时到原点的距离都会发生变化，而这个变化是确定的，因此可以在循环运算结束后以此补偿回来，这样的话我们就同时将（ρ,θ）都计算出来了。

想进一步深入学习的可以阅读 John Stephen Walther 于2000年发表在 Journal of VLSI signal processing systems for signal, image and video technology上的综述性文章“The Story of Unified Cordic”。