可配置FFT IP核的实现及基础教程

针对FFT算法基于FPGA实现可配置的IP核。采用基于流水线结构和快速并行算法实现了蝶形运算和4k点FFT的输入点数、数据位宽、分解基自由配置。使用Verilog语言编写，利用ModelSim仿真，由ISE综合并下载，在Xilinx公司的Virtex-5 xc5vfx70t器件上以200 MHz的时钟实现验证，运算结果与其他设计的运算效率对比有一定优势。

在现代声纳、雷达、通信、图像处理等领域中，数字信号处理系统经常要进行高速、高精度的FFF运算。现场可编程逻辑阵列(FPGA)是一种可定制集成电路，具有面向数字信号处理算法的物理结构。用FPGA实现FFT处理器具有硬件系统简单、功耗低的优点，同时具有开发时间较短、成本较低的优势。基于FPGA实现的数字信号处理系统具有较高的实时性和嵌入性，并能方便地实现系统集成与功能扩展。基于FPGA的硬件实现FFT通常有两种方法：(1)并行方法，其采用多个蝶形处理器并行运算，能对较高的数据采样率进行运算，但其硬件规模较大，当在FPGA上要实现较大点数的FFT时较为困难。(2)串行方法，采用一个蝶形处理器完成运算，使用的逻辑资源较少，但运算速度较慢。本文在串行方法的基础上实现了一种在FPGA上实现的可配置FFT IP核，具有输入点数可配置(实现0～4 096点自由配置)、数据位宽可配置、分解基可配置的特性。

1 原理分析

自从基2快速算法出现以来，人们仍在不断寻求更快的算法。基4 FFT算法比最初的基2 FFT算法更快，但从理论上讲，用较大的基数还可进一步减少运算次数，但要以程序(或硬件)变得更复杂为代价。提高FFF处理速度的4个主要技术途径是采用流水线结构、并行运算、增加蝶形处理单元数目和高基数结构。

1.1 基2算法基本原理
点数N是2的整数次幂，将x(n)先按n的奇偶分成两组

1.2 基4算法基本原理
与基2算法类似，对于N点有限长序列x(n)的DFT按照时域分解展开有

2 可配置FFT IP核硬件结构

现有的FFT IP核在硬件实现时不具备并行度可配置能力，只提供全循环、全流水、循环展开与流水结合等形式下的某种特定实现，可重用性较差，难以适应不同的计算吞吐量和对计算资源和计算时间的需求。可配置FFT IP核技术实现FFT算法流水、循环等并行化参数的可配置问题，兼顾FFT转换点数、输入输出数据位宽、蝶形运算基数、输入输出FIFO深度的可配置，满足不同应用条件下IP复用的需求，适应各种环境和数据吞吐量的FFT运算。可配置FFTIP核功能组成如图1所示。

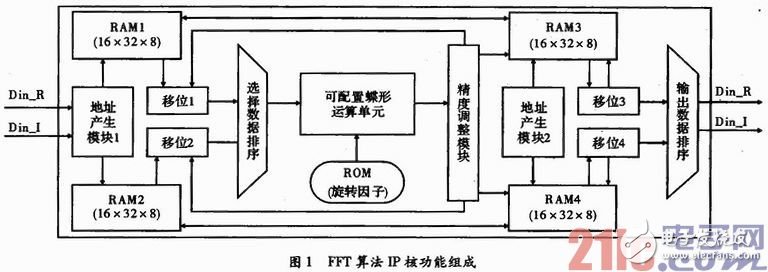
如图1所示，该IP主要包括RAM、ROM、地址产生模块、移位模块、选择数据排序模块、可配置蝶形运算单元、精度调整模块和输出数据排序模块，Din_R和Din_I是FFT输入数据的实部和虚部，Dout_R和Dout_I是FFT变换结果的实部和虚部。RAM1和RAM2存储了FFT迭代过程中的输入数据，RAM3和RAM4存储了FFT迭代过程中的计算结果，RAM1和RAM2、RAM3和RAM4均为乒乓结构。地址产生模块主要产生向RAM写入数据和从RAM读出数据的地址。ROM中存储了FFT需要的旋转因子。

2.1 IP核整体方案
设计可配置FFT处理，其整体结构如图2所示，设计采用基2蝶形和基4蝶形运算两种配置方式，供用户选择。输入数据实部和虚部分开存储，需4个RAM，为实现对连续流输入可连续流输出，其模块构成如图2所示。

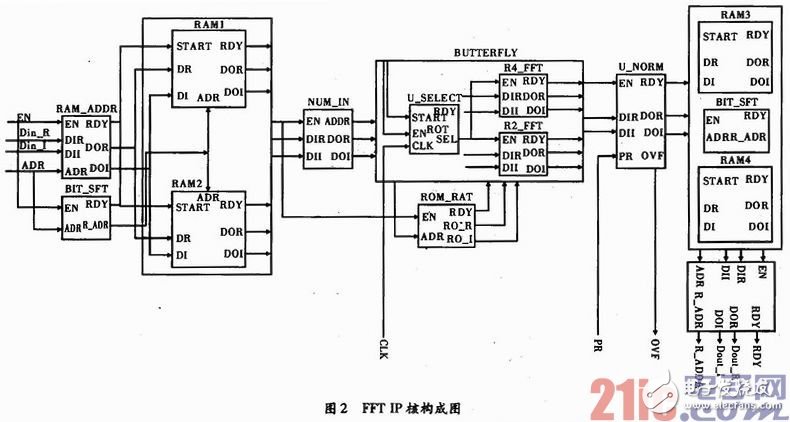
如图2所示，外部输入数据的实数部分Din_R、虚数部分Din_I，以及输入数据的地址信号ADR，首先进入RAM_ADDR单元，选择合适的时钟周期将不同点数的原始数据送入RAM单元，当输入数据的实数和虚数以及其地址准备好的时候，RDY输出1。BIT_SFT单元完成输入数据地址的移位变换，实现奇偶分离。当数据地址准备好时，RDY输出1，当RAM_ADDR或BIT_SFT这两个单元中的一个单元准备好时，便可触发RAM单元，将外部数据写入到RAM的指定地址。RAM中的数据符合可配置点数要求后，进入NUM_IN单元，其中输出的数据DOR/DOI就是符合基2蝶形或基4蝶形运算的数据顺序。这些原始数据进入蝶形运算单元BUTTERFLY，蝶形单元通过U_SELECT单元选择蝶形运算的分解基，实现基2蝶形运算、基4蝶形运算的可配置功能。其中R4_FFT是基4蝶形运算单元，B2_FFT是基2蝶形运算单元，蝶形运算过程中所需的旋转因子存储在ROM_RAT单元中，根据选择不同分解基的蝶形运算，BUTIERFLY单元产生相应的地址，选择其计算过程中的旋转因子。当蝶形运算完成后，结果数据进入U_CNORM单元，进行顺序调整和精度处理;其中PR信号是用户指定的精度信号，PR[1：0]可提供3种精度，OVF信号是数据溢出信号，若置1表明FFT结果数据超出了表示范围，则要按照截位处理以保证数据准确。当数据输入完成后，结果数据进入NUM_OUT单元，由于DIT算法输出结果以倒序形式输出，所有需要NUM_OUT进行地址调整，FFT变换结束后的结果实数部分Dout_R，虚数部分是Dout_I，地址信号是R_ADDR，以正确的顺序和形式输出。

2.2 可配置蝶形单元模块
在FFT IP核的蝶形运算单元设计中，蝶形单元的运算过程：第一个时钟周期是将下结点与旋转因子复乘的实数乘法进行计算;第二个时钟周期是将复乘中的实数进行加减运算;在第三个时钟周期是计算复乘结果与上结点的加减运算，即将蝶形运算单元的结果输出。可配置蝶形运算通过在基2和基4两种分解基之间切换来实现，其模块图如图3所示。

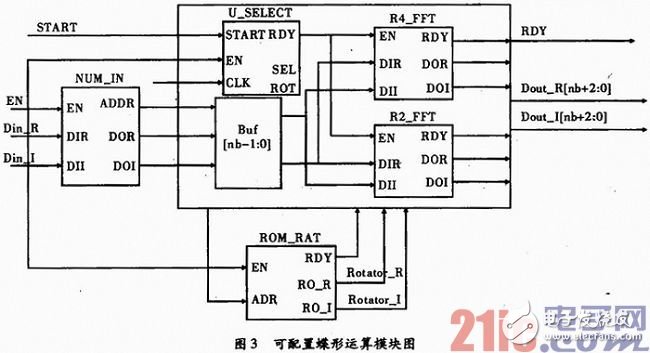
如图3所示，数据输入时能信号EN信号置1，则整个蝶形运算单元的数据输入模块NUM_IN、旋转因子模块ROM_RAT、分解基选择模块U_SELECT进入使能状态;START信号置1，则分解基选择单元U_SELECT模块开始进入状态机。根据用户设置，如果选择基2算法蝶形运算单元，则将输入数据的实部和虚部送入R2_FFT模块;如果选择基4算法蝶形运算单元，则将输入数据的实部和虚部送入R4_FFT模块;如果选择混合基，则需要在状态机中加入判断条件，准确控制分支。当蝶形运算完成时，FFT运算结果数据的实数部分Dout_R[nb+2：0]，虚数部分Dout_I[nb+2：0]比输入数据的位数[nb：0]扩展了3位，用于精度调整模块进行精度控制。

蝶形运算的旋转因子存储在ROM_RAT中，其中存储了基4运算和基2运算的旋转因子，实部和虚部分开存储，通过外部信号EN对其使能，为控制ROM存储空间的占用，不同分解基的旋转因子可公用，通过地址信号ADR选取控制。

3 仿真、综合结果分析与验证

将设计的IP核进行基于ModelSim的仿真，设置时钟频率为200 MHz，数据位宽为36位，在基2和基4两种分解基下，分析1 024点和4 096点的运算效率，其仿真图像如下所示。

图4是1 024，点的基2算法仿真结果，在这种算法下完成数据录入的时间点为113.1μs，完成结果输出的时间点为123.4μs，运算时间为10.3μs。图5是1 024点的基4算法仿真结果，在该种算法下完成数据录入的时间点51.3μs，完成结果输出的时间点是61.6μs，运算时间为8.3 μs。

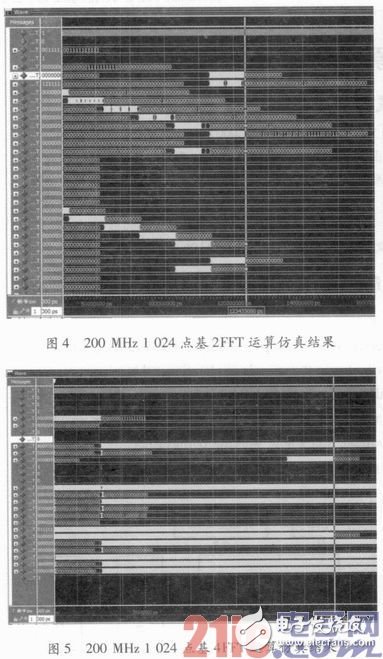
图6是4 096点的基2算法仿真结果，在这种算法下完成数据录入的时间点533.1μs，完成结果输出的时间点是574.1μs，运算时间为40 μs。图7是4096点的基4算法仿真结果，在该种算法下完成数据录入的时间点为245.7 μs，完成结果输出的时间点是286.9μs，运算时间为41.2μs。

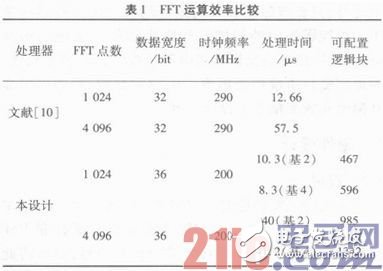
板级验证选用Xilinx公司的Virtex-5 xc5vfx70t器件进行综合、布局布线和时序分析。将得到的数据与其他设计实现进行比较，其消耗的资源，以及在200 MHz时钟情况下不同点数的FFT处理器进行一次处理需要的时间，与文献换算后得到的数值对比如表1所示。

4 结束语

本文设计的可配置FFT IP核具有灵活性强、容易扩展和设计可复用的特点，实现分解基可配置、位宽可配置、输入输出点数可配置。从验证结果可以看出，本文数据的可配置IP核具有结构简单及占用硬件资源适当的特点，在FPGA中以实现高速数字信号处理，在处理速度和灵活性方面更有优势。随着处理点数的增加，其优越性将更加明显。