FPGA数学基础分析及与CORDIC算法计算方式对比

FPGA的最大优势之一是您能够利用其嵌入式DSP模块解决最棘手的数学传递函数。多项式近似法就是此方面的良方。

由于其灵活性与高性能，FPGA已经在众多需要计算复杂数学题或传递函数的工业、科研、军事及其它应用中找到用武之地。苛刻的精度要求与计算时延在更关键的应用中并不少见。

在采用FPGA实现数学函数时，工程师一般选择定点数学（参见：赛灵思中国通讯第80期的《FPGA数学基础》， docs/xcell80/44?e=2232228/2002872 ）。另外，您还可以采用CORDIC等许多算法计算超越函数（参见：赛灵思中国通讯第79期的《如何在FPGA中运用CORDIC算法》， publications/archives/xcel l/Xcell79.pdf )。

不过，在遇到极为复杂的数学函数时，与在FPGA之中实现精确需求函数相比，还有更高效的方法进行处理。为了理解这些变通方法 – 尤其是其中的多项式近似法，我们首先需要定义相关问题。

设置问题

FPGA中负责监控铂电阻温度计（PRT）并把PRT电阻转换成温度的复杂数学传递函数就是这样一个例子。这种转换一般采用Callendar-Van Dusen方程实现。通过以下该方程的简化形式，可以确定温度介于0 ℃~660 ℃之间。

式中，R0 为0 ℃时的电阻，a 与b 是PRT的系数，而t 则是温度。

现实中，我们希望从电阻转换到温度。为此，我们需要调整该方程，确保得出的结果是给定电阻下的温度。大多数采用PRT的系统都会设计电子装置、采用电子电路测量PRT的电阻，然后利用FPGA、通过调整后的下式计算温度。

在FPGA中实现此方程即使是经验丰富的FPGA工程师也会望而却步。参考温度绘制所获得的电阻可以获得图1所示图形。从图中可以清晰看出响应的非线性。

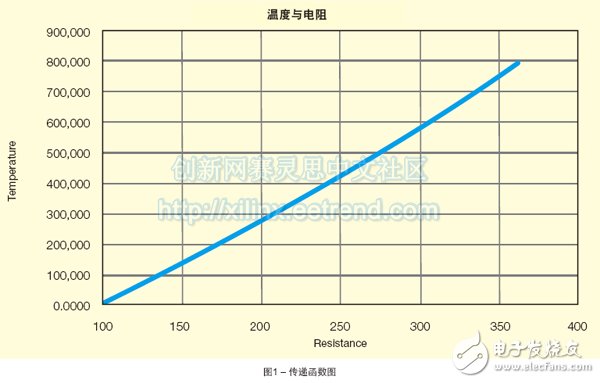
直接在FPGA中实现调整后的传递函数会在实际所需设计工作量以及验证方面面临着巨大挑战（确保精度以及跨边界与极端条件函数）。许多工程师会想方设法实现函数，以便减少设计与验证工作量，从而控制项目进度。一个可行的方法是采用查找表保存曲线中的一系列点，同时提供LUT所含点之间的线性插值。

根据相关精度要求和保存在查找表中的元素数量，这种方法有可能满足需求。但是，您仍然需要在设计中包含线性插值函数。此函数在数学上非常复杂，而且往往包含一个非二次幂除法，其会进一步增加复杂性。

利用FPGA资源

相反，您还可以利用另一种方法实现此类传递函数，那就是利用FPGA的本身特性。赛灵思 Spartan-6与7系列Artix、Kintex与Virtex等新型FPGA不仅仅只包含传统查找表和触发器，还具有内置DSP Slice、Block RAM、分布式RAM、PCIe®等众多高级IP硬核以及以太网端点、高速串行链路等。

由于其提供的48位累加器，工程师通常把DSP Slice称为DSP48s。不过，这些Slice还提供25 x 18位宽乘法器、加/减功能以及众多其它功能。您可以利用这些内部RAM结构和DSP Slice更轻松实现传递函数。

多项式近似法

利用FPGA具有丰富DSP与RAM的结构的一种方法是多项式近似法。为了使用此方法，您必须首先绘出数学函数图，在MATLAB或Excel等数学程序中涵盖输入值范围。然后您可以在相关数据集中添加多项式趋势线，然后可以在FPGA中实现该趋势线的等式，以取代复杂数学函数，只要趋势线等式符合精度要求。

如果一个多项式方程无法针对整个传递函数输入范围提供足够精度，则可以添加更多方程。只要生成一系列在相关输入范围使用的多项式常数，您就能够继续依赖此方法。

能够添加多项式趋势线的数学程序大部分都允许您选择阶次或多项式项的数量。阶次越高，则配合越准确——但是您需要在FPGA中实现更多的项。在针对传递函数示例实施此过程时，我们是采用Microsoft Excel，我们已经获得了图2所示趋势线与等式。本例中采用4次多项式方程。

在获得了适合我们希望实现的传递函数的多项式之后，我们可以采用相同分析工具（在本例中为Excel）针对原始传递函数仔细检查精度。在所述监控温度的例子中，最终测量精度可能会是+/-1C，这并非苛刻的精度要求。尽管如此，根据测量范围和您实现的传递函数，可能证实仍然很难仅用一个多项式方程实现。我们该如何解决这个问题呢？

根据输入值选择的多条趋势线

如果一个多项式方程无法针对整个传递函数输入范围提供足够精度，则可以添加更多方程。只要生成一系列在相关输入范围使用的多项式常数，您就能够继续使用此方法。因此，一旦输入值超出特定范围，则加载一个新的常数集合。

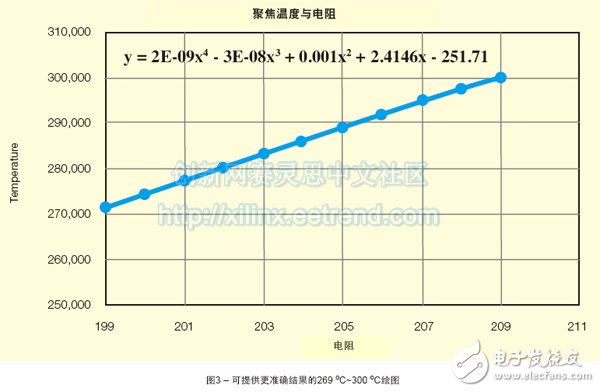
下面继续探讨温度例子，第一个多项式方程可以在0 ℃~268 ℃范围内提供+/-1 ℃的精度。对于许多应用此精度已经足够。假设我们需要达到300 ℃的更广泛运行范围与容差，则意味着我们最初的方法无法满足设计要求。利用分段方法我们能够解决上述问题，即绘出269 ℃~300 ℃范围的图形并且获得能够为此输出范围提供更高精度的不同多项式方程（见图3）。

总之，此实现方法采用第一套多项式常数，直到输入值超出与268 ℃对应的预先计算范围。超出该范围之后则采用第二套常数保持精度要求。

这样您就能够把传递函数分为一系列片段，以便达到预期精度。您可以选择跨传递函数均匀分隔这些片段，也就是说，可以把它们分为均等于X的10分段。另外，您也可以不均匀分隔，而是按实现所需精度的要求进行分段，集中精力关注较难达到精度的传递函数部分。

就决定您实现方案时需要考虑的利弊权衡而言，应当牢记的是均匀方法比非均匀方法会占用更大的内存空间。根据您所实现的传递函数，采用非均匀方法可能会节省大量资源。

如何对比？

当然，如前所述，其它方法也可以用于实现传递函数。多项式近似法之外最常用的四种方法分别是软件程序、查找表、带插值的查找表以及CORDIC。

由于需要添加处理器（会相应增加设计复杂性、材料清单成本等），采用软件计算传递函数会使系统架构复杂化。即使设计团队采用赛灵思Zynq-7000 All Programmable SoC等片上系统弥补上述缺陷，仍然会存在难题。对新手而言，用软件计算传递函数比在逻辑电路中实现需要花费多得多的时间，从而会降低系统响应时间。事实上，传递函数（诸如我们示例设计中所用的）的计算是一个典型的例子，应该由Zynq SoC可编程逻辑端负责处理。

第二种方法（即采用含有输入预算值的查找表）的效果随输入值范围与宽度变化而改变。有时会很快造成非常庞大的LUT，其会占用FPGA内部大量的RAM容量。根据相关FPGA，此方法可能需要的资源供不应求，也有可能造成与设计中其它模块竟用资源。当然，这种方法的有利之处是能够很快算出结果。

第三种潜在方法（带插值的查找表）是我们前面谈到过的一种方法，它试图减少整套LUT方法所需的内存位置数量。此方法需要工程师在FPGA内编写线性插值函数，而这项工作多少有点棘手。不过，它仍然比CORDIC这个最后选项简单得多。

CORDIC算法能够实现超越函数，如：正弦、余弦、乘法、除法、平方根等。因此，利用CORDIC算法与基本数学模块的组合能够准确实现传递函数。此方法可以实现更高精度。但是，对于复杂的传递函数，这种好处需要付出增加设计与验证时间的代价。当然这对采用该方法实现的器件的工作频率会有影响。

因此，多项式近似法是四种备选方案的折中，其能够很好地平衡性能、精度与实现资源占用。

实现简便性

每位工程师都希望创造出能够最佳利益器件资源的FPGA。多项式近似法使您能够受益于FPGA提供的丰富乘法器与RAM环境，同时能够利用这些资源轻松实现看似极其复杂的数学传递函数。