matlab中如何定义向量

　   Matlab中生成向量的三种方法

　    在Matlab中，如何才能生成向量，生成向量的方法又有多少种？相信这是每一个初学者都想知道的问题。这里小编将向大家详细介绍Matlab中生成向量的三种方法。

　　方法一：直接输入法

　　1这是最简单的向量生成法，我们只需按照向量的格式输入就可以了。如我们要生成向量A=［7，8，9，4，5，6］;这里A是个一维向量，其中的分量是7，8，9，4，5，6。

　　

　　方法二：冒号生成法

　　1这种方法适用于元素与元素之间存在等距步长（差值）的情况，即当元素间呈等差数列时可以使用。冒号生成法，其语法格式为：

　　1.向量名=［第一个元素数值：步长：最后一个元素的数值］；

　　2.向量名=第一个元素数值：步长：最后一个元素的数值

　　如我们要生成向量A=［0，2，4，6，8，10］，如图所示：

　　

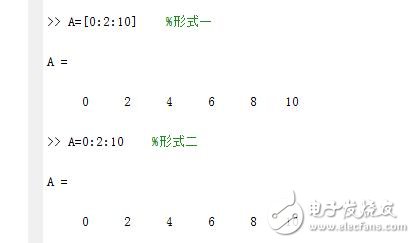
　　方法三：线性等分法

　　这种方法与冒号生成法有点相似，都是利用元素间的等差值来实现，但与冒号生成法又有些不同，不同的是线性等分法是利用函数的形式来实现的。语法格式如下：

　　向量名=linespace（第一个元素数值：最后一个元素数值：向量位数）;

　　如我们要将0～10的所有元素划分为一组6维的向量：

　　

　　matlab中如何定义向量

　　1、预置（preallocation）是编写MATLAB程序比较重要的一个因素，在数组比较大的时候，是否进行预置程序运行时间相差几十倍甚至几百几千倍都很常见。所以使用

　　A=zero（1，n）;

　　或者A=zero（n，1）;

　　进行预置通常很重要（如果n不大倒可以不做）。

　　2、提高MATLAB程序效率的另一个要点是向量化（Vectorization）代替显式循环。向量化表达式主要使用点运算操作符。例如，就楼主的问题而言，可以很简单的写成

　　A=x.^（1:n）;

　　省略了 for 循环，对于程序效率也会有很大提升。关于点运算更详细的介绍，可以看一下参考资料的链接中我以前回答的问题。

　　matlab向量定义方法：

　　1.向量的普通定义方法

　　向量的常见格式有以下三种：

　　v1=1:N; %格式1

　　v2=x1:dx:x2 ； %格式2

　　v3=x4：-dx:x3; %格式3

　　参数说明：

　　v1，v2，v3是返回的向量名。格式1中的向量的步长等于1，向量v1的最小值和最大值分贝是1和N，此种格式常用于循环指标的定义。格式2中的设定向量间隔步长是dx，向量的v2的最小值和最大值分别是x1和x2.格式3中的向量的步长等于-dx，它是一个负数，而向量的最大值和最小值分别是x4和x3。所有的返回向量都是行向量。在v1的定义的步长缺省，这是步长等于1，而向量的v2的生成语句中，步长等于dx.

　　2.用linspace函数定义向量的方法

　　函数linspace可以生成两个数之间的等间隔向量，其调用格式如下：

　　v1=linspace（x1，x2）; %格式1

　　v2=linspace（x1，x2，N）; %格式2

　　参数说明：

　　v1和v2是返回的函数名。在格式1中，x1和x2是向量的两个端点，向量元素个数是100。在格式2中，x1和x2表示向量的两个端点，N用于指定的元素个数。当N是一个小数的时候，matlab将把N进行向0取整，即fix（N）;当N时负数的时候，返回的向量v2将等于x1.同时x1和x2的大小关系人任意时，matlab自动调整正负步长，x1作为向量的起点，x2作为向量的终点。所有返回的向量都是行向量。

　　当linspace的输入参数N缺省时，生成的向量长度是100，我们可以任意指定。

　　3.用logspace函数定义向量的方法

　　函数logspace可以用来产生一个对数向量，其调用的格式如下：

　　v1=logspace（x1，x2）; %格式1

　　v2=logspace（x1，x2，n）; %格式2

　　参数说明：v1和v2是返回的对数向量。x1和x2用来控制端点，返回向量的两个端点的大小为10^1和10^2.格式1中的向量长度是50.格式2中的n用于指定向量的元素个数。函数logspace的计算过程是先得到x1和 x2之间的等间距向量，然后计算10^（linspace（x1，x2，n）），因此函数logspace得到的向量不是等间距向量，取对数后才是等距的。

　　4.用randperm函数来定义向量

　　函数randperm可以用于产生一个元素为从1到N的随机自然序列，其调用的格式如下：

　　rand（‘state’，s）

　　v=randperm（N）;

　　参数说明：

　　s用于设定随机数的状态，这样程序每次执行的结果都是一样的，我们可以改变S的值以便取到不同的随机数。N用来定义随机向量的中的最大整数。