噪声和图像信号A/D 转换器深入解读

周立功教授新书《面向AMetal框架与接口的编程（上）》，对AMetal框架进行了详细介绍，通过阅读这本书，你可以学到高度复用的软件设计原则和面向接口编程的开发思想，聚焦自己的“核心域”，改变自己的编程思维，实现企业和个人的共同进步。

第五章为深入浅出AMetal，本文内容为5.7 A/D 转换器。

5.7 A/D 转换器

>>>  5.7.1 模数信号转换

1． 基本原理

我们经常接触的噪声和图像信号都是模拟信号，要将模拟信号转换为数字信号，必须经过采样、保持、量化与编码几个过程，详见图5.4。

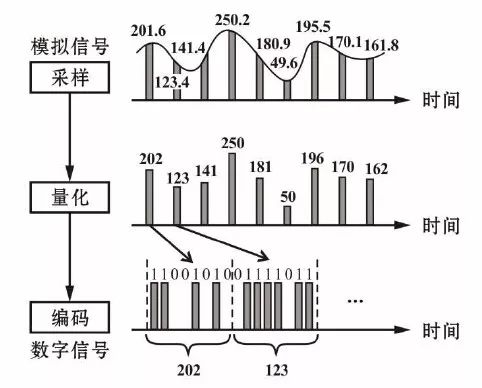
图5.4 模数信号转换示意图

将以一定的时间间隔提取信号的大小的操作称为采样，其值为样本值，提取信号大小的时间间隔越短越能正确地重现信号。由于缩短时间间隔会导致数据量增加，所以缩短时间间隔要适可而止。注意，取样频率大于或等于模拟信号中最高频率的2 倍，就能够无失真地恢复原信号。

将采样所得信号转换为数字信号往往需要一定的时间，为了给后续的量化编码电路提供一个稳定值，采样电路的输出还必须保持一段时间，而采样与保持过程都是同时完成的。虽然通过采样将在时间轴上连续的信号转换成了不连续的（离散的）信号，但采样后的信号幅度仍然是连续的值（模拟量）。此时可以在振幅方向上以某一定的间隔进行划分，决定个样本值属于哪一区间，将记在其区间的值分配给其样本值。图5.4 将区间分割为0~0.5、0.5~1.5、1.5~2.5，再用0、1、2……代表各区间，对小数点后面的值按照四舍五入处理，比如，201.6 属于201.5~202.5，则赋值202；123.4 属于122.5~123.5，则赋值123，这样的操作称为量化。

量化前的信号幅度与量化后的信号幅度出现了不同，这一差值在重现信号时将会以噪声的形式表现出来，所以将此差值称为量化噪声。为了降低这种噪声，只要将量化时阶梯间的间隔减小就可以了。但减小量化间隔会引起阶梯数目的增加，导致数据量增大。所以量化的阶梯数也必须适当，可以根据所需的信噪比（S/N）确定。

将量化后的信号转换为二进制数，即用0 和1 的码组合来表示的处理过程称为编码，“1”表示有脉冲，“0”表示无脉冲。当量化级数取为64 级时，表示这些数值的二进制的位数必须是6 位；当量化级数取为256 级时，则必须用8 位二进制数表示。

2． 基准电压

基准电压就是模数转换器可以转换的最大电压，以8 位A/D 模数转换器为例，这种转换器可以将0V 到其基准电压范围内的输入电压转换为对应的数值表示。其输入电压范围分别对应4096 个数值（步长），其计算方法为：参考电压/256＝5/256＝19.5mV。

看起来这里给出的10 位A/D 的步长电压值，但上述公式还定义了该模数转化器的转换精度，无论如何所有A/D 的转换精度都低于其基准电压的精度，而提高输出精度的唯一方法只有增加定标校准电路。

现在很多MCU 都内置A/D，即可以使用电源电压作为其基准电压，也可以使用外部基准电压。如果将电源电压作为基准电压使用的话，假设该电压为5V，则对3V 输入电压的测量结果为：（输入电压/基准电压）×255＝（3/5）×255＝99H。显然，如果电源电压升高1%，则输出值为（3/5.05）×255＝97H。实际上典型电源电压的误差一般在2~3%，其变化对A/D 的输出影响是很大的。

3． 转换精度

A/D 的输出精度是由基准输入和输出字长共同决定的，输出精度定义了A/D 可以进行转换的最小电压变化。转换精度就是A/D 最小步长值，该值可以通过计算基准电压和最大转换值的比例得到。对于上面给出的使用5V 基准电压的8位A/D来说，其分辨率为19.5mV，也就是说，所有低于19.5mV 的输入电压的输出值都为0，在19.5mV~39mV 之间的输入电压的输出值为1，而在39mV~58.6mV 之间的输入电压的输出值为3，以此类推。

提高分辨率的一种方法是降低基准电压，如果将基准电压从5V 降到2.5V，则分辨率上升到2.5/256＝9.7mV，但最高测量电压降到了2.5V。而不降低基准电压又能提高分辨率的唯一方法是增加A/D 的数字位数，对于使用5V 基准电压的12 位A/D 来说，其输出范围可达4096，其分辨率为1.22mV。

在实际的应用场合是有噪音的，显然该12 位A/D 会将系统中1.22mV 的噪音作为其输入电压进行转换。如果输入信号带有10mV 的噪音电压，则只能通过对噪音样本进行多次采样并对采样结果进行平均处理，否则该转换器无法对10mV 的真实输入电压进行响应。

4． 累积精度

如果在放大器前端使用误差5%的电阻，则该误差将会导致12 位A/D 无法正常工作。也就是说，A/D 的测量精度一定小于其转换误差、基准电压误差与所有模拟放大器误差的累计之和。虽然转换精度会受到器件误差的制约，但通过对每个系统单独进行定标，也能够得到较为满意的输出精度。如果使用精确的定标电压作为标准输入，且借助存储在MCU 程序中的定标电压常数对所有输入进行纠正，则可以有效地提高转换精度，但无论如何无法对温漂或器件老化而带来的影响进行校正。

5． 基准源选型

引起电压基准输出电压背离标称值的主要因素是：初始精度、温度系数与噪声，以及长期漂移等，因此在选择一个电压基准时，需根据系统要求的分辨率精度、供电电压、工作温度范围等情况综合考虑，不能简单地以单个参数为选择条件。

比如，要求12 位A/D 分辨到1LSB，即相当于1/2¹²=244ppm。如果工作温度范围在10℃，那么一个初始精度为0.01%（相当于100ppm），温度系数为10ppm/℃（温度范围内偏移100ppm）的基准已能满足系统的精度要求，因为基准引起的总误差为200ppm，但如果工作温度范围扩大到15℃以上，该基准就不适用了。

6． 常用基准源

（1）初始精度的确定

初始精度的选择取决于系统的精度要求，对于数据采集系统来说，如果采用n 位的ADC，那么其满刻度分辨率为1/2ⁿ，若要求达到1LSB 的精度，则电压基准的初始精度为：

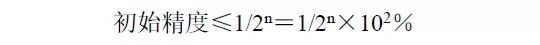
如果考虑到其它误差的影响，则实际的初始精度要选得比上式更高一些，比如，按1/2LSB 的分辨率精度来计算，即上式所得结果再除以2，即：

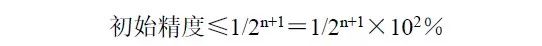
（2）温度系数的确定

温度系数是选择电压基准另一个重要的参数，除了与系统要求的精度有关外，温度系数还与系统的工作温度范围有直接的关系。对于数据采集系统来说，假设所用ADC 的位数是n，要求达到1LSB 的精度，工作温度范围是ΔT，那么基准的温度系数TC 可由下式确定：

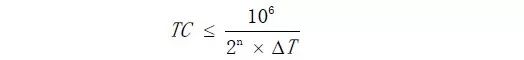
同样地，考虑到其它误差的影响，实际的TC 值还要选得比上式更小一些。温度范围ΔT通常以25℃为基准来计算，以工业温度范围-40℃~+85℃为例，ΔT 可取60℃（85℃-25℃），因为制造商通常在25℃附近将基准因温度变化引起的误差调到最小。

如图5.5 所示是一个十分有用的速查工具，它以25℃为变化基准，温度在1℃~00℃变化时，8~20 位ADC 在1LSB 分辨精度的要求下，将所需基准的TC 值绘制成图，由该图表可迅速查得所需的TC 值。

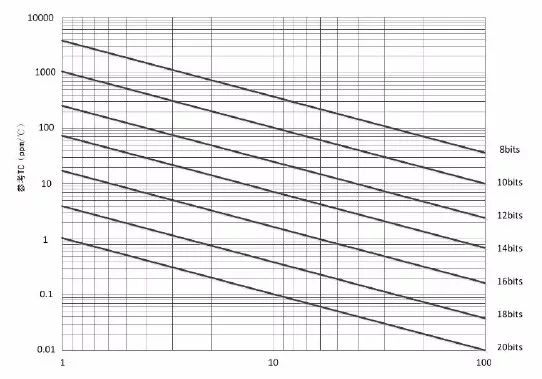
图5.5 系统精度与基准温度系数TC 的关系

TL431 和REF3325/3330 均为典型的电压基准源产品，详见表5.19。TL431 的输出电压仅用两个电阻就可以在2.5~36V 范围内实现连续可调，负载电流1~100mA。在可调压电源、开关电源、运放电路常用它代替稳压二极管。REF3325输出2.5V，REF3330 输出3.0V。

表5.19 电压基准源选型参数表

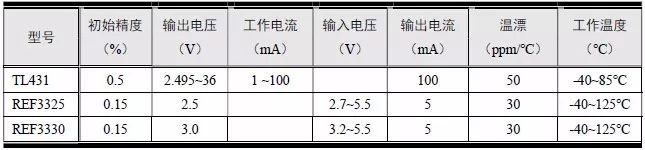
REF33xx 是一种低功耗、低压差、高精密度的电压基准产品，采用小型的SC70-3 和SOT23-3 封装。体积小和功耗低（最大电流为5μA）的特点使得REF33xx 系列产品成为众多便携式和电池供电应用的最佳选择。在负载正常的情况下，REF33xx 系列产品可在高于指定输出电压180mV 的电源电压下工作，但REF3312 除外，因为它的最小电源电压为1.8V。

从初始精度和温漂特性来看，REF3325/3330 均优于TL431，但是TL431 的输出电压范围很宽，且工作电流范围很大，甚至可以代替一些LDO。由于基准的初始精度和温漂特性是影响系统整体精度的关键参数，因此它们都不能用于高精密的采集系统和高分辨率的场合。而对于12bits的AD 来说，由于精度要求在0.1%左右的采集系统，到底选哪个型号呢？测量系统的初始精度，均可通过对系统校准消除初始精度引入的误差；对于温漂的选择，必须参考1LSB 分辨精度来进行选择，详见图5.6。如果不是工作在严苛环境下，通常工作温度为-10℃~50℃，温度变化在60℃，如果考虑0.1%系统精度，温度特性低于50ppm，则选择REF3325/3330。

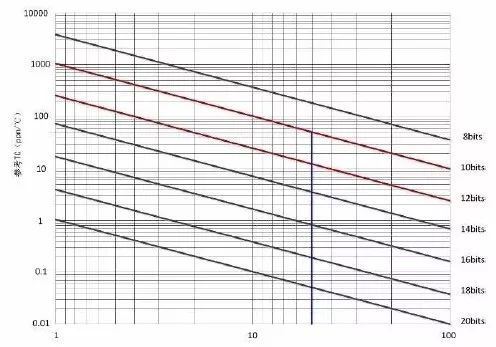
图5.6 12bits 系统基准选择

>>>  5.7.2 初始化

在使用ADC 通用接口前，必须先完成ADC 的初始化，以获取标准的ADC 实例句柄。LPC82x 仅包含一个ADC（ADC0），为方便用户使用，AMetal 提供了与ADC0 对应的实例初始化函数，其函数原型为：

函数的返回值为am_adc_handle_t 类型的ADC 实例句柄，该句柄将作为ADC 通用接口中handle 参数的实参。类型am_adc_handle_t（am_adc.h）定义如下：

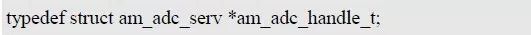
因为函数返回的ADC 实例句柄仅作为参数传递给ADC 通用接口，不需要对该句柄作其它任何操作，因此完全不需要对该类型作任何了解。需要特别注意的是，若函数返回的实例句柄的值为NULL，则表明初始化失败，该实例句柄不能被使用。

如需使用ADC0，则直接调用ADC0 实例初始化函即可完成ADC0 的初始化，并获取对应的实例句柄：

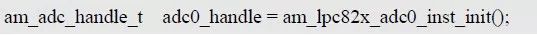
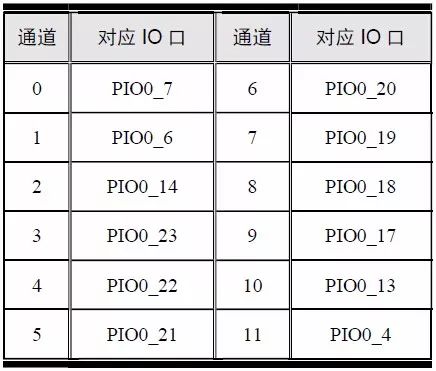
ADC0 共支持12 个通道，可以采集12 路模拟信号进行模数转换，每路模拟信号通过LPC824 的相应I/O 口输入到ADC0 中，各通道对应的I/O 口详见表5.20。

表5.20 各通道对应的I/O 口

>>>  5.7.3 接口函数

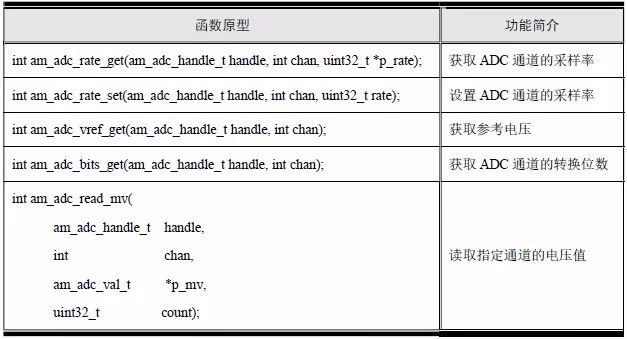
AMetal 提供了5 个ADC 相关的接口函数，详见表5.21。

表5.21 ADC 通用接口函数

1． 获取ADC 通道的采样率

获取当前ADC 通道的采样率。其函数原型为：

获取到的采样率的单位为Samples/s。如果返回AM_OK，说明获取成功；如果返回-AM_EINVAL，说明因参数无效导致获取失败，其相应的代码详见程序清单5.87。

程序清单5.87 am_adc_rate_get()范例程序

参数无效是由于handle 不是标准的ADC handle 或者通道号不支持造成的。

2． 设置ADC 通道的采样率

设置ADC 通道的采样率。实际采样率可能与设置的采样率存在差异，实际采样率可由am_adc_rate_get()函数获取。注意，在一个ADC 中，所有通道的采样率往往是一样的，因此设置其中一个通道的采样率时，可能会影响其它通道的采样率。其函数原型为：

如果返回AM_OK，说明设置成功；如果返回-AM_EINVAL，说明因参数无效导致设置失败，其相应的代码详见程序清单5.88。

程序清单5.88 am_adc_rate_set()范例程序

3． 获取ADC 通道的参考电压

获取ADC 通道的参考电压，其函数原型为：

如果返回值大于0，表示获取成功，其值即为参考电压（单位：mV）；如果返回-AM_EINVAL，说明因参数无效导致获取失败，其相应的代码详见程序清单5.89。

程序清单5.89 am_adc_vref_get()范例程序

4. 获取ADC 通道的转换位数

获取ADC 通道的转换位数，其函数原型为：

如果返回值大于0，表示获取成功，其值即为转换位数；如果返回-AM_EINVAL，说明因参数无效导致获取失败，其相应的代码详见程序清单5.90。

程序清单5.90 am_adc_bits_get()范例程序

5. 读取指定通道的电压值

直接读取ADC 通道的电压值（单位：mV），该函数会等到电压值读取完毕后返回。其函数原型为：

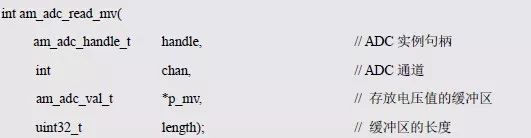
其中p_mv 是指向存放电压值的缓冲区，类型am_adc_val_t 在am_adc.h 中定义，即：

length 表示缓冲区的长度，决定了实际获取电压值的个数。如要返回AM_OK，表示读取通道电压值成功，相应缓冲区中已经填充好了读取到的电压值；如果返回-AM_EINVAL，说明因参数无效导致获取失败，其相应的代码详见程序清单5.91。

程序清单5.91 am_adc_read_mv()范例程序

>>>  5.7.4 温度采集

1． 电压采集

热敏电阻器属于敏感元件类型，按照温度系数的不同可分为正温度系数热敏电阻器（PTC）和负温度系数热敏电阻器（NTC）。热敏电阻器的典型特点是对温度敏感，在不同的温度下其电阻值不一样。正温度系数热敏电阻器（PTC）在温度越高时电阻值越大，负温度系数热敏电阻器在温度越高时电阻值越小。

AM824-Core 上有一个负温度系数热敏电阻器RT1，硬件电路详见图5.7。热敏电阻RT1 和2KΩ的R14 构成了分压电路，选用MF52E-103F3435FB-A，C8 使电路输出更加稳定。当测温范围在0~85℃时，电阻变化范围为27.6~1.45KΩ。当温度变化时，热敏电阻的阻值发生变化，单片机采集到的ADC 值也会发生变化。只要将J6 通过跳线帽短接，则R14 电阻的电压直接通过PIO0_19 输入到了ADC的通道7，即可使用ADC 采集其电压值。

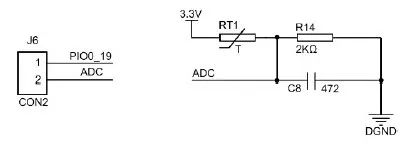
图5.7 热敏电阻电路

如程序清单5.92 所示的ntc.c 的两个函数，其中的一个用于初始化，另一个用于读取电压值。由于最终的接口还不确定，所以只创建了ntc.h。

程序清单5.92 采集电压值相关函数编写（ntc.c）

ntc_init()仅用于初始化ADC，获取一个标准的ADC 实例句柄。ntc_vol_get()用于获取ADC 通道7 对应的电压值，使用了am_adc_read_mv()函数。

为了使结果更加可信，电压采集时使用了中值平均滤波法（防脉冲干扰平均滤波法），即去掉采样数据中的最大值和最小值，再取余下数据的平均值作为最终结果。程序中，首先使用am_adc_read_mv()函数采集了12 个电压值，然后将所有电压值求和，并找出最大值和最小值，最后从和值中减去最大值和最小值后除以10 作为电压采集值并返回。

2． 获取阻值

假设采集的电压值为vol，通过R_T1 和R₁₄ 分压后，则有：

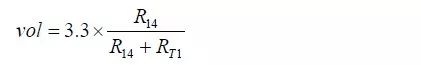
通过简单转换后可得：

利用该公式，可以将采集的电压值转换为RT1 的电阻值，详见程序清单5.93，同样将程序直接添加到ntc.c 中。

程序清单5.93 获取热敏电阻的阻值（ntc.c）

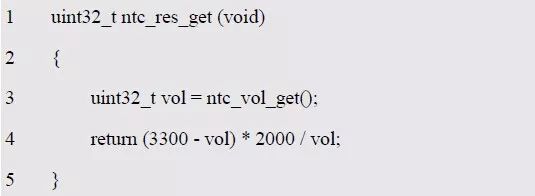
为了避免小数计算，电压的单位统一为毫伏（mV），电阻的单位统一为欧姆（Ω）。

3． 阻值与温度的关系

在获取热敏电阻阻值后，将如何找到与该电阻值对应的温度呢？不妨先从分析热敏电阻阻值与温度的关系开始。负温度系数热敏电阻的电阻值（RT）和温度（T）呈指数关系：

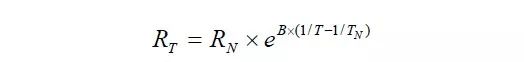
其中，R_T 是在温度T（单位为K，即开尔文）时的NTC 热敏电阻阻值，R_N 是在额定温度T_N（K）的NTC 热敏电阻阻值，B 为NTC 热敏电阻的材料常数，又叫热敏指数。由于该关系式是经验公式，因此只在额定温度 T_N 或额定电阻阻值 R_N 的有限范围内才具有一定的精确度。

如何得到材料常数B 的值呢？显然，只能通过实验测得。假定在实验环境下，测得在温度 T1 （ K ）时的零功率电阻值为RT1，在温度 T2 （ K ）时的零功率电阻值为RT2。零功率电阻是指在某一温度下测量热敏电阻值时，加在热敏电阻上的功耗极低，低到因其功耗引起的热敏电阻阻值变化可以忽略不计。额定零功率电阻是在环境温度25℃条件下测得的零功率电阻值，标记为R25，通常所说NTC 热敏电阻阻值就是指该值。

根据T1、R_T1、T₂、R_T2 和温度与电阻值的关系式，可以得到：

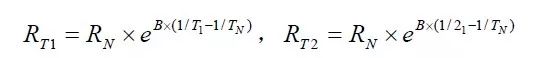
将两个等式相除可得：

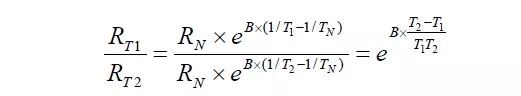
等式两边同时对e 取对数（ln）可得：

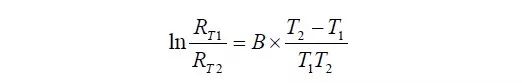
经过变换，可以得到B 值的计算公式为：

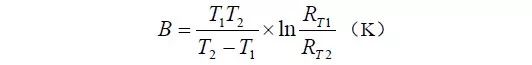
由此可见，只要测得两个温度点对应的零功率电阻值，就可以求得B 值。由于精确的测量需要有高精度的温度测量仪和高精度的电阻测量仪，一般条件下很难完成，因此，厂家往往都会提供一些温度点对应的零功率电阻值。比如，AM824-Core 使用的热敏电阻，厂家提供了两个温度点对应的零功率电阻值：R25 = 10000Ω，R85 = 1451Ω。

根据这两个温度值，即可求得B 值：

注意，表达式中的温度都是以开尔文（K）为单位的，因此需要将摄氏度（℃）转换为开尔文温度。其转换关系为：

当求得B 值后，可以使用电阻值和温度的关系式求得某温度下的电阻值。阻值与温度的关系式中RN 为在额定温度TN（K）下的阻值，可以直接使用R25 对应的值，即RN=10000Ω，TN=（25+273.15）K。以60℃为例计算对应的阻值：

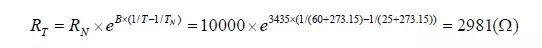
由此可见，上述计算过程是非常繁琐的，且还要涉及到复杂的指数运算，所以往往会采用查表法。即先将各个温度对应的电阻值存储到一个表格中，当需要使用时直接查表即可。

AM824-Core 的热敏电阻，厂家提供了如表5.22 所示的R-T 表。根据实际应用场合，这里仅列出了-20℃~ 87℃对应的电阻值，而实际上该热敏电阻支持-40℃~125℃的温度测量。

表5.22 热敏电阻R-T 表

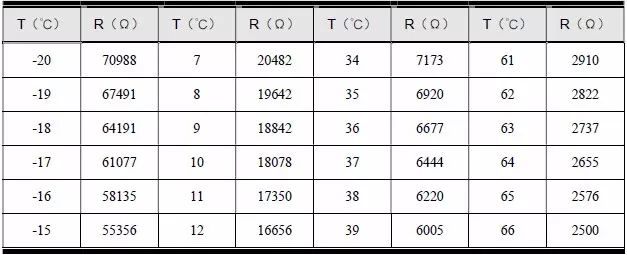
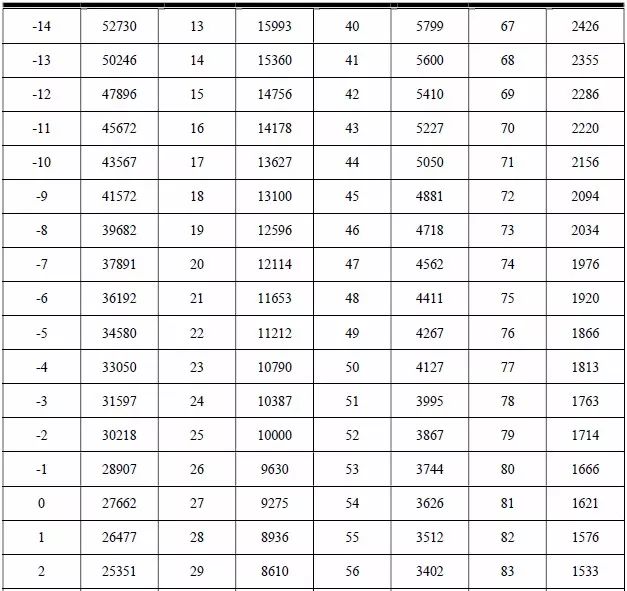
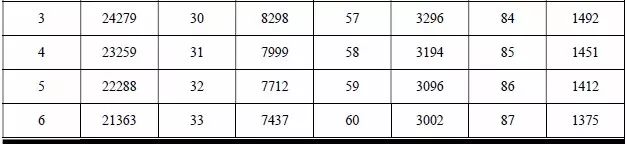
通过查表可知60℃对应的阻值为3002Ω，而计算出来的值却是2981Ω。由于前面的公式仅仅是经验公式，计算值与实测值往往会存在少量差异，但总体上是非常相近的，即2981Ω最接近60℃。由于温度是连续的，且以1℃为间距，因此仅需一维数组即可存储所有的阻值，即数组的0 号元素对应-20℃的阻值，107 号元素对应87℃的阻值。要想获得温度对应的阻值，则将温度值加上20 作为数组索引即可。

由于最大阻值为70988Ω，因此每个阻值需要一个32 位的数据来保存，则数组元素的类型设定为uint32_t 类型。-20℃~87℃共计对应108 个阻值，数组大小即为108，共计108个4 字节存储单元，即108*4 = 423 字节。注意，表格中仅-20℃和-19℃对应的阻值超过了65535，其它温度值对应的阻值均可用16 位来表示。因此可以做一些特殊的处理，比如，将-20℃和-19℃对应的阻值单独保存。如果测温范围不包含这两个温度，则可以去掉这两个温度值对应的阻值。保存温度对应阻值的ntc.c 详见程序清单5.94。

程序清单5.94 定义保存各个温度值对应阻值的数组

由于数组的起始元素为-20℃对应的阻值，因此对应温度与数组索引的关系如下：

• 对应温度=数组索引－20

• 数组索引=对应温度＋20

由于数组索引与温度存在20 的差值，如果需得到25℃对应的阻值，则应该在使用温度值的基础上加上20 作为数组的索引。即：

4. 获取温度值

虽然已经得到了热敏电阻阻值与温度的对应关系，但是如何获取阻值对应的温度呢？如果阻值对应的温度刚好是整数，即阻值会与数组中某个元素相等，则只需要扫描一遍数组，如果扫描到阻值相等，即可得到对应的温度，详见程序清单5.95。

程序清单5.95 获取温度值（1）

虽然该程序实现起来很简单，却不实用，因为得到的阻值恰好是整数温度的概率太小了。而事实上得到的阻值往往处于某个区间之内，比如，7500Ω对应的温度范围为32℃~ 33℃，那么该如何确定其温度值呢？7500Ω与32℃对应的7712Ω相差212Ω，与33℃对应的7437Ω相差63Ω，显然与33℃更加接近，那是不是直接取33℃就好了呢？如果对精度要求不高，得到的温度全为整数值，如果希望更加精确，比如，要求精确到小数点后两位？

尽管指数关系是非线性关系，其对应的阻值-温度关系图是曲线图，但可以将这一曲线分解为若干小段，将每一小段中的阻值-温度关系近似为线性关系。如将1℃温度区间内的阻值-温度关系近似为线性关系进行处理。假设已知区间的两个端点（R1，T1）、(R2，T2)，那么使用已知两点求直线方程的方法，很容易得到阻值R（R1≤R≤R2）对应的温度为：

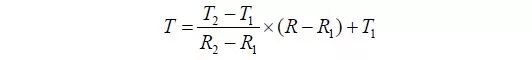
对于上述例子来说，若测得电阻阻值为7500Ω，则区间的两个端点为（7712，32）和（7437，33），使用上述式子可得到温度值：

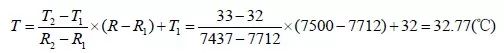
显然，这样求得的温度更加精确，其相应的代码详见程序清单5.96。

程序清单5.96 根据温度区间获取温度值

程序中使用的是带符号数，而电阻值是用无符号数表示的，因此必须将无符号的电阻值事先存放到有符号数中再进行计算。当无符号数与有符号数混合运算时，由于无符号数优先级高，因此会先将有符号数转换为无符号数再作运算，特别是在有负数参与运算的场合，往往会得到意想不到的结果。比如：

为什么结果等于0？因为a 是无符号数，在计算a/b 时，按照无符号数计算，则会先将-32转换为无符号数，即4294967264，96 整除一个这个大的数，结果自然就为0 了。同时，为了避免小数的计算，将运算结果扩大了256 倍。由于测量的温度范围为-20℃~87℃，即便扩大256 倍后也不会超过16 位带符号数的范围，因此最终返回一个16 位的带符号数。

为何要扩大256 倍而不是100 倍呢？当然，100 倍更好理解，如果扩大100 倍，即表示保留2 位小数，最小表示数值为0.01。其实扩大256 倍也是一样的，其最小表示数值为1/256= 0.00390625，具有更高的精度。前面我们已经使用的LM75B 采集温度值，读取温度值的lm75_read()函数返回的实际测量温度值也扩大了256 倍。这样一来，如果这里返回的温度值同样也扩大256 倍，则之前的程序就完全可以复用了。

为了使用ntc_temp_get_from_range()函数得到温度值，还需要找出阻值对应温度所在的温度区间。如何获取区间呢？由于阻值是顺序递减的，最简单的方法就是顺序寻找，只要找到测得的电阻值大于阻值表中某个温度对应的阻值时，即可确定其处在的区间。如顺序寻找阻值7500 的区间时，找到温度为33℃对应的阻值7437 时，发现比其小，则说明33℃为其右边界，左边界为上一个温度值，即32℃，其相应的代码详见程序清单5.97。

程序清单5.97 获取温度值（2）

实际上，当前的搜索方法效率太低，如果温度是87℃，则要搜索108 次，直到将数组元素全部遍历一遍为止。由于阻值是顺序递减的，则不妨用二分法。即每次与中间的数比较，根据比较结果即可将搜索范围缩小一半，接着继续与新的搜索范围中的中间值比较，同样可以根据比较结果将搜索范围缩小一半，依此类推，每次比较都可以直接将搜索范围缩小一半。

下面还是以7500Ω为例，数组元素总共有108 个，索引为0 ~ 107，用两个变量low 和high 分别表示搜索范围的下界和上界，mid 表示中间位置。

(1) 初始时，则low = 0，high = 107，中间位置即为（low+high）/2 = 53（直接按照C语言整数除法），53 位置（即温度33℃，直接查表5.22）对应的阻值为7437，7437 小于7500，因此搜索范围锁定至上半部分，因此更新high = 53；

(2) 继续搜索，low = 0，high = 53，mid = 26，26 位置对应的阻值为21363，21363 大于7500，因此搜索范围一定在后半部分，更新low = 26；

(3) low = 26，high = 53，mid = 39，39 位置对应的阻值为12596，12596 大于7500，因此搜索范围还是在后半部分，更新low = 39；

(4) low = 39，high = 53，mid = 46，46 位置对应的阻值为9630，9630 大于7500，因此搜索范围还是在后半部分，更新low = 46；

(5) low = 46，high = 53，mid = 49，49 位置对应的阻值为8610，8610 大于7500，因此搜索范围还是在后半部分，更新low = 49；

(6) low = 49，high = 53，mid = 51，51 位置对应的阻值为7999，7999 大于7500，因此搜索范围还是在后半部分，更新low = 51；

(7) low = 51，high = 53，mid = 52，52 位置对应的阻值为7712，7712 大于7500，因此搜索范围还是在后半部分，更新low = 52。至此，由于low 与high 之间只差1，无法再继续分成两部分，因此，确定要找的值一定在位置52 与53 之间，也就是阻值对应的温度范围为32℃~ 33℃，到此为止搜索结束。

针对108 个元素，按照二分法搜索，最多搜索7 次，其相应的代码详见程序清单5.98。

程序清单5.98 获取温度值（3）

至此，即可直接调用ntc_temp_read()获取温度值。相关函数编写完毕，将ntc_init()和ntc_temp_read()函数声明详见程序清单5.99（ntc.h），其具体实现详见程序清单5.100（ntc.c）。

程序清单5.99 ntc.h 文件内容

程序清单5.100 ntc.c 文件内容

ntc.c 相比于之前的代码，新增了两个变量：

(1) 新增变量res_val_num 用于表示数组元素的个数

在范围搜索时，将之前的固定值107 修改为数组元素个数，这样一来数组元素就可以继续向后增加，比如，增加至-20℃~125℃，则所有代码都无需任何修改。

(2) 新增变量temp_start 用于表示阻值表的起始温度值

之前的代码固定了起始温度为-20℃，如果向前扩展温度范围为-40℃~125℃，则程序必须做相应的修改。当增加该变量后，向前扩展温度范围时，仅需修改该变量的值即可，此时数组的起始元素就是temp_start 温度对应的阻值，因此对应温度与数组索引存在如下关系：

对应温度 = 数组索引＋temp_start，数组索引 = 对应温度－temp_start

范例程序可以直接修改此前编写的“智能温控仪”程序，使用热敏电阻获取温度值替换之前的LM75 获取温度值。仅需修改3 行代码即可：“#include "lm75.h" 修改为 #include"ntc.h"，am_main()函数中的lm75_init()修改为ntc_init()，am_main()函数中的lm75_read()修改为ntc_temp_read()”，而其它复杂的键盘处理和数码管显示等均可复用。

---