在FPGA或其它可编程器件内开发数学函数所使用的规则与方法详解

基于FPGA 的解决方案具有众多优势，其中之一就是能够针对眼前的问题采用最佳的方式来进行数学算法。例如，如果响应时间至关重要，我们就简化数学运算步骤。如果注重运算结果的精度，我们就使用更多的位来确保达到预期的精度。当然，很多新型FPGA 还具有嵌入式乘法器和DSP slice 的优势，可用于在目标器件中获得最佳的实现性能。

让我们了解一下在FPGA 或其它可编程器件内开发数学函数所使用的规则与方法。

数字的表示方式

在一种设计方案中可以使用两种数字表示方式，即定点数与浮点数。定点表示法中小数点位置固定不变，可以直接进行算数运算。定点数的主要缺点是如果要表示一个较大的数或者得到一个更精确的小数值，就需要使用若干个位。定点数由两部分构成：整数和小数。

浮点表示法中小数点位置随数值的大小在不同位置浮动。浮点数同样也可分为两部分：指数和尾数。这种表示方法类似于科学计数法，科学技术法是将一个数表示为A 乘以10 的B 次幂，其中A 为尾数、B 为指数。但在浮点数中，指数部分的基数是2，即A 乘以2 的B次幂。IEEE/ANSI 754-1985 标准对浮点数表示法进行了标准化。基本IEEE 浮点数使用8 位指数和24 位尾数。

由于浮点数的表示法存在一定的复杂性，我们作为设计人员应尽可能多地采用定点表示法。上述浮点数采用补码表示法， 其无符号数表示范围介于0.0 ～255.9906375 之间，有符号数表示范围介于-128.9906375～ 127.9906375 之间。您在一种设计方案中既可以使用无符号数也可以使用有符号数，这通常取决于您所用的算法。无符号数的表示范围为0 ～ 2n-1，始终表示正数。

相比之下，有符号数的表示范围则取决于所采用的编码方案，即符号数值表示法（即原码）、1 的补码（即反码）或2 的补码（即补码）。

原码中最左边的位表示数的符号（0 为正，1 为负）。其余的位表示数值的大小。在这种表示方法中，正数和负数的绝对值相同，但是符号位不同。因此，原码方案中存在正零和负零。

正数的反码与其原码的无符号数相同。负数的反码为正数按位取反。

补码是使用最广泛的有符号数编码方案。这里与其它两种编码方案一样，正数与无符号数的表示形式相同，而负数的二进制表达式与绝对值相同的正数相加后等于0。计算负数补码时，首先将正数按位取反，然后再加1。补码允许您将两个数的减法按照加法来处理。补码可以表示的范围是：

将一个数转换为补码格式的方法是按从右至左的顺序按位遍历，从遇到的第一个“1”开始将二进制位按位取反，而之前的二进制位保持不变。

定点运算

在定点数中，通常用x 和y 来区分整数位和小数位，其中x 表示整数位的数量，y 表示小数位的数量。例如，8，8 表示8 个整数位和8 个小数位；16，0 表示16 个整数位和0 个小数位。在很多情况下，您通常需要在设计阶段根据浮点算法转换来确定所需的整数和小数位数量。得益于FPGA 的灵活性，我们可以表达任意二进制长度的定点数；整数位的数量取决于需要存储的最大整数值，而小数位的数量取决于最终结果的精度。我们利用以下公式来确定整数位的数量：

例如，要表示0.0 ～ 423.0 范围内的数值，所需整数位的数量为：

这表示您需要9 个整数位，可以代表0 ～ 511 范围内的数。利用16 个位来表示这个数时，可以有7 个位用于表示小数。利用下面的等式计算这种表达方式所能提供的精度：

您可以增加小数位的数量，进而提高定点数的精度。在设计过程中，我们有时希望只存储小数（0，16）， 这主要取决于您希望将精度提高到多少。利用216 进行扩展可能依然无法达到足够高的精度。这种情况下，您可以用2 的幂次方来放大这个数，使这个数可以用16 个位来表示。然后，您可以在下一阶段删除这个比例因子。例如，为了用16 个位来表示1.45309806319x10-4，第一步需要将这个数与216 相乘。

只存储结果的整数部分（9）将导致这个数的实际存储值为1.37329101563x10-4（9 / 65536）。需要存储的数值与实际存储的数值之间差值较大，可能导致出现无法接受的错误计算结果。您可以按照比例因子2 来放大这个数，以获取更精确的结果。结果介于32768-65535之间，因此仍然可以用一个16 位的数字来存储。利用此前存储1.45309806319x10-4 的实例，将这个数与比例因子228 相乘将产生一个可以用16 个位来存储的数，并使预期的数值具有更高的精度。

假定在接下来的计算过程中您可以解决用比例因子228进行放大的问题， 那么结果的整数部分将给予您1.45308673382x10-4 的存储结果，并使得计算结果具有更高精度。例如，将已扩展的数与一个16 个位格式为4，12 的数相乘，产生了4，40（28 + 12）形式的结果。但是，这个结果将以32 位来存储。

定点规则

在执行加法、减法或除法时，2 个数的小数点必须对齐。这就是说您只可以将一个表示格式为x，8 的数与另一个表示格式也为x，8 的数相加、相减或相除。对具有不同格式的x 和y 进行算术运算时，您首先应保证小数点对齐。为了对齐不同格式的数字，您有两个选择：将带有更多整数位的数与2X 相乘，或者将具有最小整数位的数除以2X。但是，除法会降低结果的精度，还可能导致结果超出容许公差。由于所有的数都可以利用两种形式来存储，这样您在FPGA 中通过移位操作可以很方便地对数进行放大或缩小，其中左移或右移1 位分别放大或缩小了1 倍，实现十进制小数点的对齐。为了对两个格式分别为8，8和9，7 的两个数相加，如果可以接受最低有效位的丢失，则您可以利用比例因子21 来放大格式为9，7 的数，也可以将格式为8，8 的数缩小至格式为9，7。

例如，您打算将234.58 和312.732 这两个数相加，而它们分别以8，8 和9，7 的格式来存储。第一步，确定实际相加的16 位数。

从上可以看出，两个加数分别为60052 和40029。但是，在相加之前，您必须对齐小数点。通过放大带有更多整数位的数来对齐十进制小数点，您必须利用因子21 来放大9，7 格式的数。

然后，您通过执行加法来计算结果：

以10，8 格式（140110 / 28）表示，则为547.3046875。

当两个数相乘时，您无需对齐小数点，因为乘法提供了范围是X1 + X2，Y1 + Y2 的结果。将格式分别为14，2 和10，6 的两个数相乘将得出一个整数位为24，小数位为8 的结果。

通过与除数的倒数相乘这种方法，在一个式子中您可以采用与小数相乘来代替除法。这种途径可以显著降低设计的复杂性。例如，将212.732（以9，7（40029）格式来表示）除以15，第一步是计算除数的倒数。

这个倒数必须被放大，以16 位数的形式来表示。

将这两个数相乘，得出格式为9，23 的结果。

相除结果为：

当预期的结果是20.8488，如果结果的精度不够高，则您可以利用一个更大的比例因子来放大这个倒数，以得到更精确的结果。因此，当可以与一个数的倒数相乘时，永远不要除以这个数。

溢出问题

在实现算法时，结果必须不大于结果寄存器可以存储的最大值。否则，就会发生溢出。当溢出发生时，存储结果就会有误，最高几位会丢失。溢出的最简单实例是将2个16 位的数相加，每个数的值都是65535，然后将结果存储在16 位寄存器中。

上述计算将使得这个16 位结果寄存器中的值为65534，但这个结果不正确。防止溢出的最简单方式是确定数学运算允许的最大值，利用这个方程来确定所需结果寄存器的大小。

如果您正在开发一个平均器，计算50 个16 位输入值的平均值，则可以计算所需结果寄存器的大小。

仍然利用同一个方程，需要一个22 位结果寄存器来防止溢出的发生。您也必须注意，在处理有符号数时，如果遇到了负数，应该避免发生溢出。仍然利用此前的平均器实例，计算10 个有符号长度为16 位的数的平均值，返回一个16 位的结果。

因为很方便地将结果与除数倒数的扩展值相乘，您将这个数与1/10 • 65536 = 6554 相乘来确定平均值。

这个数除以216 等于-32770， 但16 位的输出结果无法正确地表示这个数。因此，模块的设计过程必须考虑溢出，必须检测溢出，以确保不会输出不正确的结果。

现实世界的实现方式

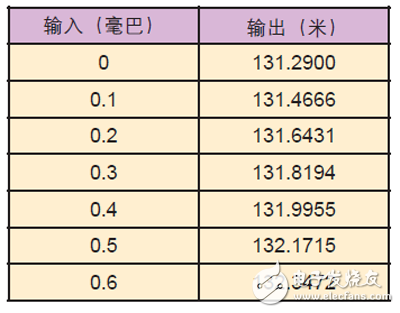
假设您正在设计一个模块，用于实现一个转换气压的转移函数，其中气压的单位是毫巴，海拔的单位是米。

输入值的范围是0 ～ 10 毫巴，分辨率是0.1 毫巴。模块输出要求精确到+/-0.01 米。因为模块规范没有确定输入刻度，您可以通过下列等式来计算。

因此，为了实现最高的精度，您应将输入数据的格式设置为4 个整数位，12 个小数位。开发这个模块的下一步任务就是利用未扩展值并通过电子数据表计算出整个输入范围内转换函数的预期结果。如果输入范围过大而无法获得合理的结果，则计算可接受的点数量。例如， 您使用100 个条目来确定整个输入范围的预期结果。在您计算出最初的非扩展预期值之后，下一步是确定正确的常数比例因子，利用扩展值来计算预期的输出结果。为了实现最高的精度，您应利用不同的因子来放大该式中每个常数。

多项式中第一个常数（A）的比例因子为：

多项式中第二个常数（B）的比例因子为：

因为最后的多项式常数（C）是一个纯小数，所以利用比例因子216 来放大它。

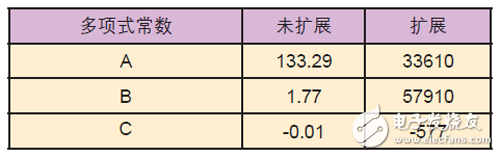
通过这些比例因子用户可以计算出扩展的电子数据表，如表1 所示。每一阶段的计算结果将得出超过16 位的结果。

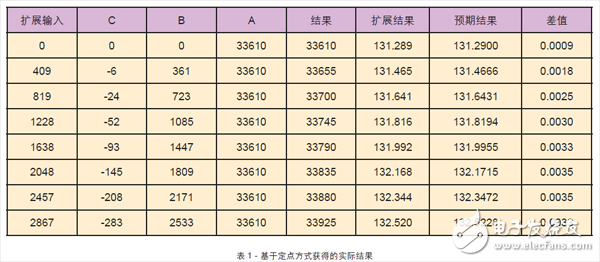
Cx2 的计算得出32 位、格式为4，12 + 4，12 = 8，24 的结果。然后与常数C 相乘，得出了48 位、格式为8，24 + 0，16 = 8，40 的结果。对于这个实例所要求的精度来说，利用40 位来表示小数有点多。因此，将这个计算结果除以232，以得出16 位、格式为8，8 的结果。在计算Bx 过程中，也将结果减小至16 位，以得出格式为5，11 的结果。

计算结果是Cx2，Bx 与A 列中对应数之和。但是，为了获得正确的结果，您首先必须扩大A 和Cx2 ，并按x，11 格式对齐小数点，或者缩小Bx 的计算结果并按8，8格式对齐小数点，最终将小数点与A 和Cx2 的计算值的小数点对齐。

在这个例子中，我们将计算结果缩小23 倍，按8，8格式来对齐小数点。这种方法简化了需要移位的数量，因此减小了实现这个实例所需逻辑单元的数量。注意如果您通过缩小来对齐小数点的方式而没有实现要求的精度时，则必须扩大A 和Cx2 的计算结果来对齐小数点。在这个实例中，计算结果扩大了28。然后，您可以缩小这个结果，将其与从未扩展值中获取的结果比较。实际计算结果和预期结果之间的差值表示精度，利用电子数据表中MAX（） 和MIN（） 命令来获得计算结果的最大误差和最小误差，而您在电子数据表条目的整个范围内都可以获取计算结果的这两个误差。

当基于电子数据表的计算结果确认了您已经实现了所要求的精度，则可以编写并仿真RTL 代码。如果需要，您可以设计一个测试平台，例如输入值与电子数据表中的数据相同。这允许您将仿真输出结果与基于电子数据表的计算结果进行比较，以确保采用了正确的RTL 实现方案。

RTL 实现方案

RTL 实例利用有符号并行数学运算在4 个时钟周期之内即可计算出结果。因为采用了有符号的并行乘法，所以应该注意到必须正确地处理由乘法产生的额外符号位。

ENTITY transfer_function IS PORT（

sys_clk ： IN std_logic;

reset ： IN std_logic;

data ： IN std_logic_vector（15 DOWNTO 0）;

new_data ： IN std_logic;

result ： OUT std_logic_vector（15 DOWNTO

0）;

new_res ： OUT std_logic）;

END ENTITY transfer_function;

ARCHITECTURE rtl OF transfer_function IS

-- this module performs the following

transfer function -0.0088x2 + 1.7673x +

131.29

-- input data is scaled 8，8， while the

output data will be scaled 8，8.

-- this module utilizes signed parallel

mathematics

TYPE control_state IS （idle， multiply，

add， result_op）;

CONSTANT c ： signed（16 DOWNTO 0） ：= to_

signed（-577，17）;

CONSTANT b ： signed（16 DOWNTO 0） ：= to_

signed（57910，17）;

CONSTANT a ： signed（16 DOWNTO 0） ：= to_

signed（33610，17）;

SIGNAL current_state ： control_state;

SIGNAL buf_data ： std_logic; --used to

detect rising edge upon the new_data

SIGNAL squared ： signed（33 DOWNTO 0）; --

register holds input squared.

SIGNAL cx2 ： signed（50 DOWNTO 0）;

--register used to hold Cx2

SIGNAL bx ： signed（33 DOWNTO 0）; --

register used to hold bx

SIGNAL res_int ： signed（16 DOWNTO 0）;

--register holding the temporary result

BEGIN

fsm ： PROCESS（reset， sys_clk）

BEGIN

IF reset = ‘1’ THEN

buf_data 《= ‘0’;

squared 《= （OTHERS =》 ‘0’）;

cx2 《= （OTHERS =》 ‘0’）;

bx 《= （OTHERS =》 ‘0’）;

result 《= （OTHERS =》 ‘0’）;

res_int 《= （OTHERS =》 ‘0’）;

new_res 《= ‘0’;

current_state 《= idle;

ELSIF rising_edge（sys_clk） THEN

buf_data 《= new_data;

CASE current_state IS

WHEN idle =》

new_res 《= ‘0’;

IF （new_data = ‘1’） AND （buf_data

= ‘0’） THEN --detect rising edge

new data

squared 《= signed（ ‘0’& data）

* signed（‘0’& data）;

current_state 《= multiply;

ELSE

squared 《= （OTHERS =》‘0’）;

current_state 《= idle;

END IF;

WHEN multiply =》

new_res 《= ‘0’;

cx2 《= （squared * c）;

bx 《= （signed（‘0’& data）* b）;

current_state 《= add;

WHEN add =》

new_res 《= ‘0’;

res_int 《= a + cx2（48 DOWNTO 32）

+

（“000”& bx（32 DOWNTO 19））;

current_state 《= result_op;

WHEN result_op =》

result 《= std_logic_vector（res_

int （res_int‘high -1 DOWNTO 0））;

new_res 《= ’0‘;

current_state 《= idle;

END CASE;

END IF;

END PROCESS;

END ARCHITECTURE rtl;

FPGA 架构成为了实现数学函数的理想工具，尽管实现算法需要具有更多的最初想法以及利用MATLAB® 或Excel 等系统级仿真工具来建模。一旦掌握了FPGA数学运算的一些基本知识，用户就可以快速地实现数学算法。