关于FPGA设计中使用CORDIC算法的教程分享

虽然CORDIC 是实现 DSP 和数学函数最重要的算法之一，但许多设计人员并不熟悉。

大多数工程师在碰到需要在 FPGA 中实现诸如正弦、余弦或开平方这样的数学函数时，首先会想到的是用查找表，可能再结合线性内插或者幂级数（如果有乘法器可用）。不过对这种工作来说，CORDIC 算法是工具库中最重要的工具之一，只是鲜有工程师知晓。

CORDIC 的意思是坐标旋转数字计算机， 是 JackVolder 在 1959 年为康维尔公司 (Convair) B-58A“盗贼”项目设计新的导航计算机时发明的。这是一种设计用于计算数学函数、三角函数和双曲函数的简单算法。

这种算法的真正优势在于只需要采用极小型的 FPGA封装就可以实现它。CORDIC 只需要一个小型查找表，加上用于执行移位和加法的逻辑。重要的是这种算法不需要专门的乘法器或除法器。

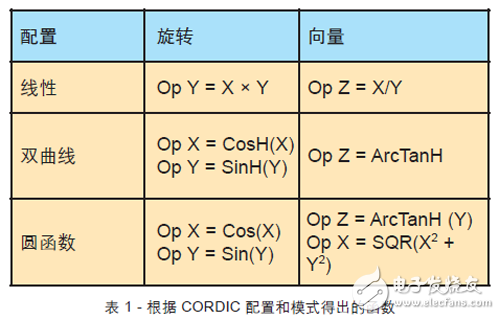
这种算法是 DSP 以及工业与控制应用最有用的工具之一，其最为常见的用途是实现如表 1 所示的传统数学函数，可在器件缺少专用乘法器或 DSP 模块的情况下提供器件所需的乘法器、除法器或更有意义的函数。举例来说，设计人员在众多小型工业控制器中使用 CORDIC 来实现数学传递函数和真正的 RMS 测量。工程师也在生物医学应用中使用 CORDIC 来进行快速傅里叶变换 (FFT) 计算，以分析多种生理信号的频谱。在本应用中，结合传统的数学函数，设计人员使用 CORDIC 实现 FFT 旋转因子。

CORDIC 详解
CORDIC 算法可以采用线性、圆或双曲线三种配置中的任何一种进行运算。而对于每种配置，算法又可以在旋转或向量任一模式下执行。在旋转模式下，输入向量按一定的角度旋转，而在向量模式下，算法将输入向量旋转到 X 轴，同时记录旋转角度。

另外，可以从 CORDIC 的输出求出其它函数。许多情况下，甚至可以使用另一个配置截然不同的 CORDIC来实现这些函数，如下所示：

下面的统一算法涵盖了 CORDIC 的所有三种配置。该算法有 X、Y 和 Z 三种输入。表 2 是根据配置预先计算的查找表值，表 3 则是根据运算模式（向量或旋转）在启动时的初始化方式。

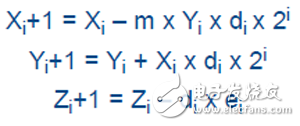
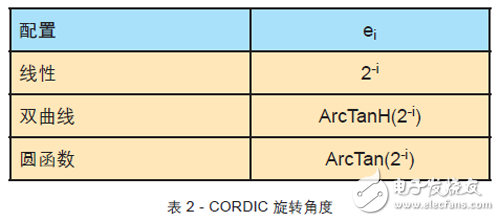
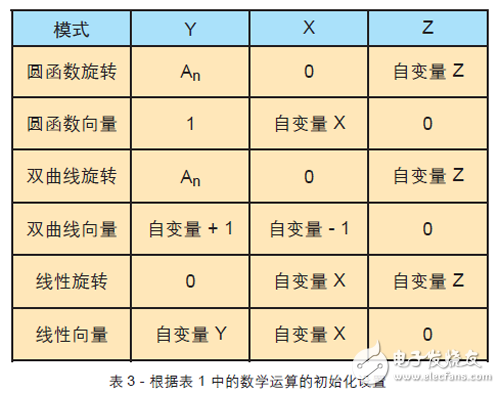
其中m表示双曲线（m=-1），线性（m=0）或旋转（m=1）配置。ei 值则为不同配置下的对应的旋转角度。ei 值一般在FPGA 中通过小查找表实现，如表 2 所示。

在这个等式中，di 为旋转方向，这取决于运算模式。在旋转模式下，如果 Zi < 0，则 di = -1，否则 di = +1；在向量模式，如果 Yi < 0，则 di = +1，否则 di = -1。

在圆函数旋转模式或双曲线旋转模式下，输出结果将有增量，这部分增量可以通过下面等式中定义的旋转次数来预先求得。

这部分增量一般反馈到算法的初始设置中，以免对结果进行后缩放。

设计人员在工作时必须牢记 CORDIC 算法只能在严格收敛域内运算。可能需要进行一定的预缩放，以确保其能够按预期执行。需要指出的是，决定执行的迭代（串行）或级数（并行）的次数越多，得到的运算结果就越准确。经验法则告诉我们，如果需要 n 位的精度，就需要进行 n 次迭代或 n 个级数。不过在横切代码前，所有这些都可以采用诸如 Excel 或 MATLAB® 等简易工具轻松完成建模，从而确保能够用选定的迭代次数得到精确的结果。

根据定义，CORDIC 算法只能在有限的输入值范围内收敛（工作）。对采用圆函数配置的 CORDIC 算法而言，只要角度不大于查找表中的角度之和（即在 -99.7°到99.7°之间）即可保证收敛。对大于这个范围的角度，必须使用三角恒等式将其转换为这个范围内的角度。采用线性配置时，其收敛亦如此。但是，要实现双曲线配置下的收敛，必须重复进行一定数量的迭代（4、13、40、K…3K+1）。在这种情况下最大输入值 θ 约为 1.118 弧度。

CORDIC 应用
设计人员在从数字信号处理和图像处理到工业控制等多种应用中采用CORDIC 算法。最基本的用法是将CORDIC 与相位累加器结合，以生成正弦波和余弦波，供 I 调制和 Q 调制使用。使用该算法生成这些波形，如果生成正确，可以实现高度的无杂散动态范围 (SFDR)。对大多数信号处理应用而言，需要良好的无杂散动态范围。

在机器人技术领域，CORDIC 被用于运动学领域，对判断机器人的关节、四肢的位置和运动非常有用。在该应用中，可以使用圆函数向量模式的 CORDIC 算法轻松将坐标值与新坐标值相加。在图像处理领域，像光照和向量旋转这样的三维运算最好选用该算法来实现。

在 EXCEL 中建模
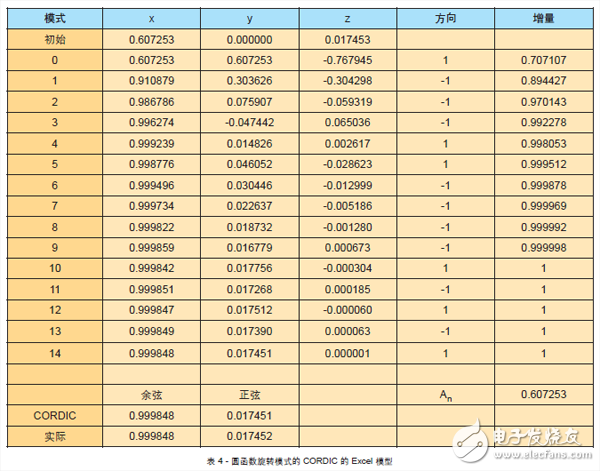
在横切代码前，建立 CORDIC 算法模型最直观的方法之一是填制简单的Excel 数据表。这样可以先用浮点数系统，再用可扩展的定点数系统为迭代次数和增量（An）建模，以便为仿真过程中的代码验证提供参考。

从表 4 的 Excel 模型中可以看到，将初始的 X 输入设为 An，可以减少结果后处理工作量。初始自变量设为 Z，单位为弧度，和结果一样。

实现 CORDIC
如果没有其他更好的选择，在 FPGA中实现 CORDIC 算法的最简单方法就是使用像赛灵思 CORE Generator®这样的工具。CORE Generator 提供了全面的接口，供用户定义 CORDIC的确切功能（旋转、向量等），如图1 所示。

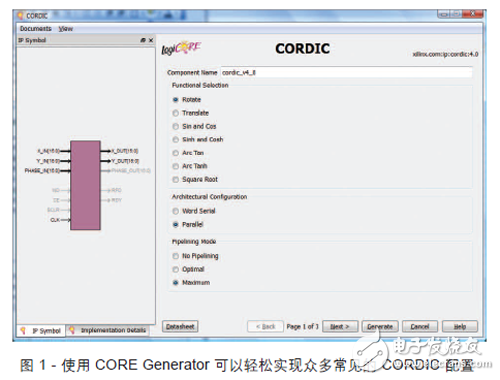
令人遗憾的是，CORE Generator 不提供 CORDIC 在线性模式下工作的选项（该工具确实提供有执行这些功能的独立内核）。不过只需要几行就可以编写出实现该算法：
LIBRARY ieee;
USE ieee.std_logic_1164.all;
USE ieee.numeric_std.all;
ENTITY synth_cordic IS PORT(
clk : IN std_logic;
resetn : IN std_logic;
z_ip : IN std_logic_vector(16 DOWNTO
0); --1,16
x_ip : IN std_logic_vector(16 DOWNTO 0);
--1,16
y_ip : IN std_logic_vector(16 DOWNTO 0);
--1,16
cos_op : OUT std_logic_vector(16 DOWNTO
0); --1,16
sin_op : OUT std_logic_vector(16 DOWNTO
0)); --1,16
END ENTITY synth_cordic;
ARCHITECTURE rtl OF synth_cordic IS

TYPE signed_array IS ARRAY (natural RANGE
<> ) OF signed(17 DOWNTO 0);

--ARCTAN Array format 1,16 in radians
CONSTANT tan_array : signed_array(0 TO 16)
:= (to_signed(51471,18),
to_signed(30385,18),
to_signed(16054,18),to_signed(8149,18),
to_signed(4090,18), to_signed(2047,18),
to_signed(1023,18), to_signed(511,18),
to_signed(255,18), to_signed(127,18),
to_signed(63,18), to_signed(31,18),

to_signed(15,18),
to_signed(7,18),to_signed(3,18),
to_signed(1,18), to_signed(0, 18));
SIGNAL x_array : signed_array(0 TO 14) :=
(OTHERS => (OTHERS =>'0'));
SIGNAL y_array : signed_array(0 TO 14) :=
(OTHERS => (OTHERS =>'0'));
SIGNAL z_array : signed_array(0 TO 14) :=
(OTHERS => (OTHERS =>'0'));
BEGIN
--convert inputs into signed format
PROCESS(resetn, clk)

BEGIN
IF resetn = '0' THEN
x_array <= (OTHERS => (OTHERS =>
'0'));
z_array <= (OTHERS => (OTHERS =>
'0'));
y_array <= (OTHERS => (OTHERS =>
'0'));
ELSIF rising_edge(clk) THEN
IF signed(z_ip)< to_signed(0,18)
THEN
x_array(x_array'low) <=
signed(x_ip) + signed('0' & y_ip);
y_array(y_array'low) <=
signed(y_ip) - signed('0' & x_ip);
z_array(z_array'low) <=
signed(z_ip) + tan_array(0);
ELSE
x_array(x_array'low) <=
signed(x_ip) - signed('0' & y_ip);
y_array(y_array'low) <=
signed(y_ip) + signed('0' & x_ip);
z_array(z_array'low) <=
signed(z_ip) - tan_array(0);
END IF;
FOR i IN 1 TO 14 LOOP
IF z_array(i-1) < to_signed(0,17)
THEN
x_array(i) <= x_array(i-1) +
(y_array(i-1)/2**i);
y_array(i) <= y_array(i-1) -
(x_array(i-1)/2**i);
z_array(i) <= z_array(i-1) +
tan_array(i);
ELSE
x_array(i) <= x_array(i-1) -
(y_array(i-1)/2**i);
y_array(i) <= y_array(i-1) +
(x_array(i-1)/2**i);
z_array(i) <= z_array(i-1) -
tan_array(i);
END IF;
END LOOP;
END IF;
END PROCESS;
cos_op <=
std_logic_vector(x_array(x_array'high)(16
DOWNTO 0));
sin_op <=
std_logic_vector(y_array(y_array'high)(16
DOWNTO 0));
END ARCHITECTURE rtl;

在 FPGA 中实现 CORDIC 有两种基础拓扑，一种是状态机法，一种是流水线法。

如果对处理时间要求不是特别严格，可以使用状态机实现该算法，每周期计算一次 CORDIC 迭代，直到完成要求的周期次数。如果需要高计算速度，并行架构则更合适。上述代码采用15 级并行旋转模式 CORDIC 计算。它使用如表 2 所示的简单圆函数模式 ArtTan(2-i) 查找表，结合简单的阵列结构实现并行级。

在五花八门的各种方法中，CORDIC 算法证明自己是一种简单且功能强大的算法，值得所有 FPGA 设计人员关注。更值得一提的是，使用内核生成工具或手动编码可以轻松实现 CORDIC。