基于OpenMP的电磁场FDTD并行方法的程序设计

随着多核技术的不断发展，并行方法已经成为一种处理较大规模问题的手段，同时在许多领域取得了成功地应用。目前，并行算法的实现主要基于两种标准：

MPI（Message Passing Interface）是一种基于消息传递并行编程模型的工业标准，主要用于分布存储体系结构的现实，是已被证实了的理想的程序设计模型;OpenMP标准，主要用于共享存储体系结构的并行编程，可实现在SMP 集群系统内多处理器的多线程并行计算。

OpenMP是一个应用程序接口，通过规范一系列的编程制导、运行库函数和环境变量来说明共享存储体系结构的并行机制，通常由于其较低的开销和相对较简单的编程而受到人们广泛的关注。

时域有限差分（FDTD）方法是模拟计算电磁场的一种基本算法。自1966年Yee首次提出以来，经过半个多世纪的发展，这一方法得到迅速发展和广泛应用。但是时域有限差分算法通常由于其串行方式使问题本身复杂化且运算较费时间而采用并行方式计算。因此，在PC机上研究并行FDTD算法问题，具有重要的理论与现实意义，可为大规模工程问题的并行化处理提供一定的方法借鉴与理论依据。本文以一维平面波在自由空间中的传播为例，讨论了采用OpenMP 技术对电磁场FDTD算法程序实现并行化的方法，并将该并行方法在三维瞬态场电偶极子辐射FDTD程序中进行了验证，也相当于对该并行方法进行了一定的推广，并通过实验证明了该并行计算的有效性。

1、电磁场理论简介

FDTD方法由微分形式的麦克斯韦（Maxwell）旋度方程出发进行离散而得到的一组时域推进公式。一维情况下，设TEM波沿z 轴方向传播，介质参数和场量均与x，y 无关，即- /-x = 0， -/ -y = 0 ，于是Maxwell方程为：

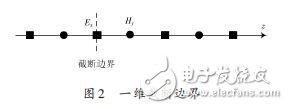
一维情况E 、H 分量空间节点取样如图1所示。

在自由空间中，σ = σm = 0 ，介质为无耗，故而可得场的FDTD迭代方程为：

为了满足数值计算的Courant稳定性条件，通常选取时间步长为 Δt 空间间隔为 δ ，FDTD截断边界条件采用一阶近似Mur，设截断边界处为Ex 节点，如图2所示，则在Ex 节点处离散，得：

式中： Ex （k - 1）为截断边界内的节点;c 在真空中为光速c0，在介质中则为截断边界处波的传播速度。

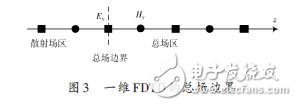
激励源采用高斯脉冲源，其表达式为Ei （t），其中τ 为常数，决定了高斯脉冲的宽度。为了使入射波限制在空间有限区域，根据等效原理，在区域分界面上设置等效面电磁流，并设分界面外的场为零。所以，在总场-散射场区的分界面上（总场边界）设置入射波电磁场的切向分量便可将入射波只引入到总场区。本实验通过在一维FDTD 的总场边界处引入高斯脉冲波，如图3所示。

2、OpenMP 并行设计

2.1 OpenMP概述

OpenMP是基于共享存储体系结构的工业标准，它不是一门独立的语言，而是对基本语言的扩展，如C/C++，Fortran语言。其编程简单，开销小，规范并制定了一系列的编译指导语句、运行库函数和环境变量。对于传统的串行代码，采用OpenMP技术并行化时无需对原程序作大的改动，只需加入一些简单的编译指导语句即可。同时，OpenMP 提供了两种粒度的并行方式：粗粒度并行和细粒度并行。OpenMP的细粒度并行是指利用OpenMP 只求解循环部分计算，又称为循环级并行。由此可见，细粒度并行是一种最为简单的并行方法。

2.2 OpenMP并行编程模型

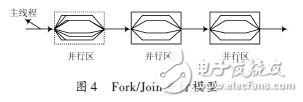
OpenMP采用标准的并行模式--Fork/Join式并行执行模式，如图4所示，在编译过程中使用编译指导语句实现并行化。在程序开始执行时，只有主线程的运行线程存在，在执行的过程中，若遇到OpenMP 的指令要求并行执行时，主线程会派生出子线程来执行并行任务。在并行执行的过程中，由主线程与派生出的子线程组成一个线程组来协同工作。在并行执行结束后，派生出的子线程退出或挂起，不再工作，控制流程回到单独的主线程中，直到下一个并行区或者程序执行完毕。

2.3 FDTD算法的并行化

在用FDTD算法模拟计算电磁场的过程中，时间步长上的迭代过程是相关联的、互相影响的，故而不能实现并行化。但是在一次迭代内部，电场与磁场的计算仅需要前一时刻的计算结果，与其他区域的电场或者磁场分量无关，各个计算过程之间没有影响、相互独立，可以实现并行化。为此，本文采用OpenMP提供的细粒度并行的方式对该算法实现并行化，即OpenMP+细粒度并行。

3、并行FDTD 性能分析

3.1 仿真算例设计

为验证FDTD算法并行的性能，以电磁波在自由空间中传播的一维FDTD 算法为例，采用OpenMP 提供的细粒度技术实现并行化。激励源采用Gauss脉冲源，其带宽为10 GHz，τ = 0.2 ns， t0 = 0.8 - τ = 0.16 ns，总场边界为z0 = 500Δz 处，Δt = τ/ 80 = 0.002 5 ns， Δt = dz/ （2c），吸收边界采用一阶近似Mur，波传播的空间区域为节点1~1 000.用统计的方法，分别测量了2 000~10 000 之间不同迭代次数的串并行时间。

3.2 并行性能测试

并行程序性能测试可由并行算法的加速比和并行效率来衡量，假设有n 个并行部件，则对加速比、效率的定义如下：

（1）加速比speedup=单一计算机运行整个程序所花费时间同一台计算机使用n 个并行部件的执行时间;

（2）效率efficiency= speedup n.

程序串并行的运行时间由OpenMP 库函数提供的OMP_get_wtime（）函数来测量。具体地，在测量串行程序运行时间时，注释掉了程序中的并行编译指导语句，并保持时间函数的位置不变。本文采用多次运行程序取稳定值的方法，分别测量并记录了不同迭代次数下的程序串并行运行时间。

3.3 测试环境

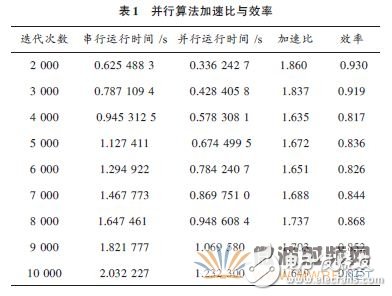
测试环境为Intel（R） Core（TM） 2 Duo CPUT5670@1.8 GHz，内存为2 GB，操作系统为WinXP SP3，开发软件为Intel Fortran 10.1.014 with vs 2005，测试结果如表1所示。

3.4 并行方法验证

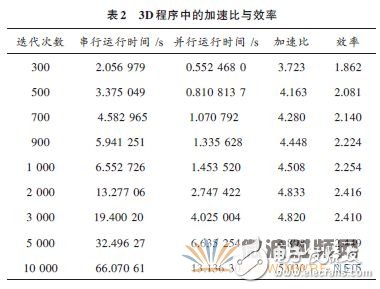
为了验证本文所采用的OpenMP 并行算法的可行性，将该并行方法应用于三维瞬态场电偶极子辐射FDTD程序中。设整个计算域空间为真空，垂直点偶极子位于计算域中心，即Ez（0，0，0），FDTD计算空间步长为5 cm，时间步长为83.333 ps，计算域为55×55×55 个元胞，截断边界为Mur吸收边界，辐射源为高斯脉冲，测量并记录了300~10 000之间不同迭代次数的串并行时间，测量结果见表2.

4、结论

本文从分析OpenMP本身的特点及编程模型入手，结合一维FDTD算法实例，采用OpenMP+细粒度并行的方式实现了并行化，并证明了基于OpenMP 的并行FDTD 算法的有效性，而且并行FDTD 算法在所选测试实例的不同迭代次数上均获得了超线性的加速比。充分利用了OpenMP共享存储体系结构的特点，避免了消息传递带来的开销，取得了较其他并行FDTD算法更快加速比和更高的效率。更值得一提的是，将该并行方法应用在三维电磁场FDTD 程序中也取得了很好的加速比和效率，可以预见，该优化方法在更复杂的算法中应用一定具有更理想的性能提升。但不足之处在于系统的可扩展性差，这是由于OpenMP 本身的特点所限制。

因此，今后的工作将放在对基于SMP 机群的MPI 与OpenMP混合编程模型的研究，从而克服系统扩展性差的缺点，进而提升系统的易用性和可移植性。