bcd码加法器

　　BCD码（Binary-Coded Decimal‎）亦称二进码十进数或二-十进制代码。用4位二进制数来表示1位十进制数中的0~9这10个数码。是一种二进制的数字编码形式，用二进制编码的十进制代码。BCD码这种编码形式利用了四个位元来储存一个十进制的数码，使二进制和十进制之间的转换得以快捷的进行。

　　这种编码技巧最常用于会计系统的设计里，因为会计制度经常需要对很长的数字串作准确的计算。相对于一般的浮点式记数法，采用BCD码，既可保存数值的精确度，又可免去使电脑作浮点运算时所耗费的时间。此外，对于其他需要高精确度的计算，BCD编码亦很常用。

　　由于十进制数共有0、1、2、……、9十个数码，因此，至少需要4位二进制码来表示1位十进制数。4位二进制码共有2^4=16种码组，在这16种代码中，可以任选10种来表示10个十进制数码，共有N=16！/［10！*（16-10）！］等于8008种方案。常用的BCD代码列于末。

　　BCD码加法器

　　在计算机内部，出于存储和计算方便的目的，采用基2码对十进制数进行重新编码，最少需要基2码的位数为log210，取整数位4 ，4位基2码有16种表示方法。

　　十进制数的几种4位编码

　　

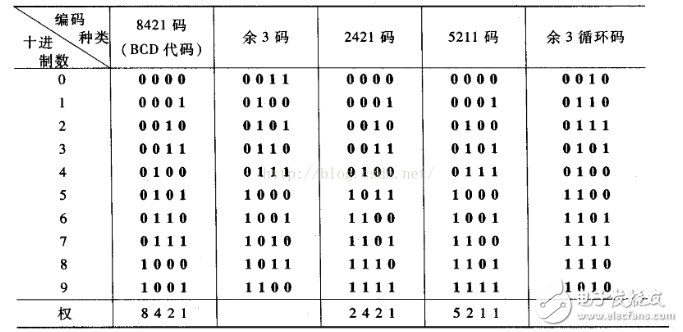
　　8421码又称BCD码，是十进制代码中最常用的一种。在这种编码方式中，每一位二值代码的1都表示一个固定数值，将每一位的1代表的十进制数加起来，得到的结果就是它所代表的十进制数码。由于代码中从左到右每一位的1分别表示8、4、2、1，所以将这种编码称为8421码。每一位的1代表的十进制数称为这一位的权。8421码中每一位的权是固定不变的，它属于恒权代码。

　　在计算机内部实现BCD码之间的算术运算要复杂一些，即在某些情况下，对加法运算的结果进行修正。修正规则如下：

　　（1） 若两个8421码数相加之和等于或小于1001，不需修正。

　　（2） 若相加和在10-15之间，一方面应向高位产生进位，本身还要进行加6修正，进位是在加6修正时产生的。

　　（3） 若相加之和在16-18之间，向高位进位会在相加过程中自己产生，对本位还要进行加6修正。

　　实验代码使用vhdl语言：

　　LIBRARY IEEE;

　　USE IEEE.STD_LOGIC_1164.ALL;

　　USE IEEE.STD_LOGIC_ARITH.ALL;

　　ENTITY bcd IS

　　PORT（ a ： UNSIGNED（4 DOWNTO 0）;

　　b ： UNSIGNED（4 DOWNTO 0）;

　　c ： OUT STD_LOGIC_VECTOR（4 DOWNTO 0）

　　）;

　　END bcd;

　　ARCHITECTURE adding OF bcd IS

　　SIGNAL sum ： STD_LOGIC_VECTOR（4 DOWNTO 0）;

　　SIGNAL co ： STD_LOGIC;

　　SIGNAL add ： integer RANGE 0 TO 31;

　　BEGIN

　　add 《= conv_integer（a+b）;

　　co 《= ‘1’ WHEN add》9 ELSE

　　‘0’;

　　sum 《= a+b+6 WHEN co=‘1’ ELSE

　　a+b;

　　c 《= sum;

　　END adding;