

基于FPGA的浮点数据格式和高效的多输入浮点乘法器结构设计
可编程逻辑
描述
1 引言
近年来,随着FPGA的发展.以及相应EDA开发软件的成熟,在FPGA上进行数字信号处理的方法正显示出巨大的优势,特别是随着高密度、高速度FPGA器件的出现,加之FPGA高度灵活的在线可编程性。使得FPGA在需要高速数字信号处理的领域得到了越来越广泛的应用。
由于浮点数具备大动态范围以及可充分使用有效位的特点,浮点乘法运算已经成为 种最基本的运算之一。其运算的速度及所占的资源直接决定了系统的处理能力。但浮点乘法运算相对于定点运算来说,运算步骤及实现电路均比较复杂。因此,如何快速地以最少逻辑资源及时钟节拍完成一次浮点运算一直是学者们长期研究的热点和难点。最基本的双输入浮点乘法器设计经过多年的发展,已经取得了大量的成果【l-2},而针对多输入浮点乘法器的专门研究却相对较少。传统的多输入浮点乘法器是采用双输入乘法器通过级联结构实现。如以四输入为例,为了尽量提高运算速度,则需要三个双输入浮点乘法器来实现,如图1所示。
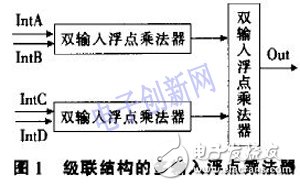
这种结构的乘法器不仅成倍增加了计算所需流水线级数。而且也成倍增加了所需的逻辑资源。在高速数字信号处理的情况下显然不合适。本文正是为了解决这一问题.针对FPGA及多输入浮点乘法器的结构特点。提出了一种更适合于在FPGA上快速实现的浮点数据格式和高效的多输入浮点乘法器结构。
下面首先介绍浮点乘法器的基本运算步骤.而后分析单精度浮点数据格式实现浮点乘法器的难点.再引出适合于FPGA实现的自定义26位浮点数据格式及高效的多输入浮点乘法器结构,最后给出在Xilinx公司Vi~ex系列芯片上的测试数据。
2 浮点乘法器的基本算法
浮点数据的格式有多种.不同格式的浮点数据在处理的流程及算法上基本相同。其中单精度(IEEE Single_Precision Std.754)浮点数据格式如图2所示。
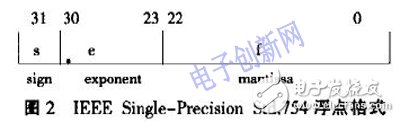
在IEEE Single_Precision标准中,数值是32-bit。其中bit-31是符号位,当其为0时表示正数,1时为负数;Bit 30-23为范围为0~255的正整数;Bit22~0表示数值的有效位。浮点数所表示的具体值可用下面的通式表示。其中当e=0,f=0时v=0,尾数(1.f)中的‘1’为隐藏位。
一般来说.浮点乘法器需要以下的操作步骤:
(1)指数相加:完成两个操作数的指数相加运算;
(2)尾数调整:将尾数f调整为1.f的补码格式;
(3)尾数相乘:完成两个操作数的尾数相乘运算;
(4)规格化:根据尾数运算结果调整指数位。并对尾数进行舍入截位操作。规格化输出结果。
第(1)步需一级8位加法操作;第(2)步中。将23位的无符号数根据符号位调整为24位的补码.需一级取反操作和一级24位的加法操作;第(3)步即完成一级24位的乘法操作;第(4)步的规格化操作也需一级8位加法操作。在这4个步骤中,第(1)步和第(2)、(3)步可并行执行。这样要完成整个浮点乘法运算需依次进行一级24位加法、一级24位乘法(同时进行8位加法操作)及一级8位的加法操作。在FPGA的实现中。运算速度主要受限于乘法操作的速度.而目前的FPGA芯片中内部集成的乘法器均为18x18位的固定结构。则1个24x24的乘法器需要由4个18x18乘法器组成(相当于两级18x18乘法操作)。显然。采用IEEE Single_Precision Std.754浮点数据格式的浮点乘法器难以达到很高的运算速度,且所需的资源较多,运算时延至少需3个时钟节拍。这样,在FPGA上实现四输入的浮点乘法功能最少也需要5~6级的流水线运算。且需12个
18x18乘法器资源。
3 自定义26位浮点数据格式
由上文分析可知.浮点乘法器的运算速度主要由FPGA内部集成的硬件乘法器决定。如果将24位的尾数修改为18位的尾数。则可在尽量保证运算精度的前提下最大限度地提高浮点乘法运算的速度,同时也可大量减少所需的乘法器资源。IEEE标准中尾数设置的隐藏位主要是考虑节约寄存器资源.而FPGA内部具有丰富的寄存器资源。如直接将尾数表示成18位的补码格式,则可减少第(2)步的运算。也即可以减少一级流水线操作。同时。在FPGA进行数字信号处理的系统中。一般处理的数据都是处理AD采样送出的信号,其分辨率一般取12-16位,取18位有效位数即可满足绝大多数的情况。由此我们定义一种新的浮点数据格式,如图3所示。

浮点数所表示的具体值可用下面的通式表示:
其中m为18位定点补码数。小数点定在最高位与次高位之间,这样m表示范围为一1≤m《1的小数:e仍为范围为0-255的正整数。且规定当m=0或e=-32时值为0。这种浮点数据格式与单精度格式的区别在于:自定义格式将原来的符号位与尾数位合成18位的补码格式定点小数,表示精度有所下降.却可大大节约乘法器资源(由4个18x18乘法器减少到1个),并极大提高运算速度(由二级18x18乘法运算减少到一级运算)。
4 高效的多输入浮点乘法器结构
由以上分析可知,传统的级联形式实现多输入浮点乘法运算在结构上有大量的无谓重复,从而不可避免地导致逻辑资源的浪费及计算时延的增加。采用自定义的26位浮点数据格式来实现浮点乘法器只需2级流水线操作.则级联结构的四输入浮点乘法器至少需4级流水线操作。仔细观察多输入浮点乘法器的特点就不难发现。只要在结构上将二输入浮点乘法器的各个步骤推广到多输入形式。就可以大量节约资源和时延。其结构框图如图4所示。
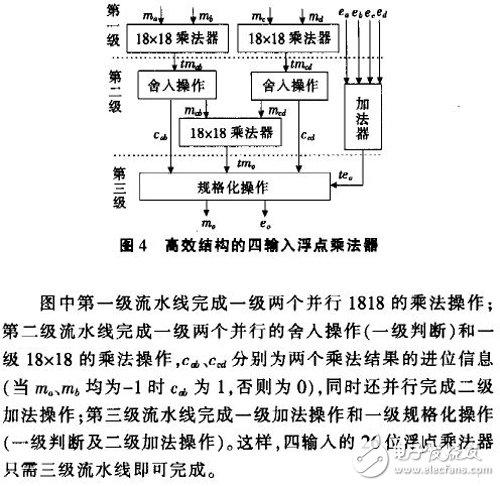
5 测试分析
我们在Xilinx公司的Virtex芯片上对本文提出的高效结构的实现代码进行了测试与仿真,测试数据如表1所示。测试采用的开发环境为ISE6.3-01i。编程语言为VHDL,综合工具为Synplify Pro v7.6.仿真工具为Modelsim 5.8b。
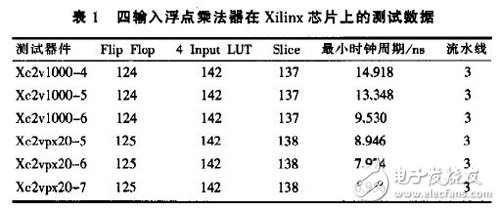
从表1中可以清楚地看到.采用新的浮点数据格式及适合于多输入浮点乘法器的高效结构,其时钟频率较高(Xc2vpx20-
7最高可达143.76MHz),只需3级流水操作,且所占用的资源也较少。可以应用于实时性高的数字信号处理场合。依据图4所设计的四输入浮点乘法器目前已成功应用于作者所从事的工程项目中。
-
modbus浮点数怎么读取2023-12-28 9440
-
单精度和双精度浮点数的区别2023-12-15 7159
-
什么是浮点数2023-02-23 5999
-
什么是浮点数?浮点数在内存中的存储2022-11-09 7185
-
谈一谈浮点数的精度问题2022-08-11 5936
-
如何在FPGA中正确处理浮点数运算2022-03-18 5936
-
怎么实现32位浮点阵列乘法器的设计?2021-05-08 2078
-
基于FPGA的高速流水线浮点乘法器该怎么设计?2019-09-03 2182
-
modbus 如何读取浮点数2018-02-08 15268
-
硬件乘法器2015-11-03 4208
-
基于FPGA的高速流水线浮点乘法器设计与实现2012-02-29 4168
-
基于FPGA 的单精度浮点数乘法器设计2010-09-29 786
-
浮点数的表示方法2009-10-13 17069
-
功能:浮点BCD码转换成格式化浮点数2009-01-19 2642
全部0条评论

快来发表一下你的评论吧 !

