

用FPGA硬件实现多路伪随机序列应用适应光学SPGD控制算法设计
可编程逻辑
描述
1 引 言
随机序列是一组满足特定统计学规律的数据,在信号理论分析中应用非常普遍。由于 精确的随机序列生成方法较为复杂,产生的随机序列不具有可重复性等特点,在很多应用 场合使用伪随机序列。伪随机序列在扩频通信、信息加密和系统测试等诸多领域中都有着 广泛的应用。在自适应光学SPGD 算法中,伪随机序列亦有相当重要的作用。
Vorontsov 等人在1997 年将SPGD 算法引入到自适应光学领域[2]。国内在近几年开始了对 SPGD 算法在自适应光学系统应用的研究,并且在计算机上用软件编程实现了算法,进行 了自适应光学的系统实验[3]。自适应光学SPGD 控制算法的研究趋势是使用专用的信号处 理硬件电路作为算法的实现平台,以获得更高的迭代速度和更好的收敛效果。Cauwenberghs等人设计了专用的模拟超大规模集成电路实现SPGD 控制算法,并且在一些应用领域进行 了实验[5]。目前自适应光学系统的规模普遍达到几十上百单元。针对多单元自适应光学系 统SPGD 控制算法的特殊要求,本文提出了一种适合于用FPGA 硬件电路产生满足算法要求的多路伪随机序列的生成方法,完成了FPGA 电路的硬件实现,并将其用于实现61 单 元自适应光学SPGD 控制算法,同时进行自适应光学的闭环实验。
2 自适应光学 SPGD 控制算法对伪随机序列的要求
SPGD(the Stochastic Parallel Gradient Descent algorithm)算法通过对多路的控制参数加 入随机并行的扰动,使用性能指标测量值的变化量与控制参数的变化量进行控制参数的梯 度估计,以迭代方式在梯度下降方向上进行控制参数的搜索。在自适应光学SPGD 算法中, 控制参数为变形镜的控制电压,随机并行的扰动通过多路伪随机序列模拟。SPGD 算法中 随机并行扰动的特性,对伪随机序列也提出了相应的要求[5]:
(1) 路数多。路数等于变形镜单元数(即变形镜上驱动单元的数目)。例如在一个61 单 元的自适应光学系统中,就需要产生61 路的伪随机序列。
(2) 伪随机序列两两相互独立。相互独立可避免变形镜各驱动单元间的相互耦合。
(3) 伪随机序列符合伯努利分布,两个样本值出现的概率各为0.5。
3 硬件电路实现伪随机序列的传统方法
传统的生成伪随机序列的方法较多,如线性反馈移位寄存器法(LFSR,可产生M 序列), 乘同余法,线性同余法,Gold 序列等[6],[7]。M 序列是一种常用的随机序列,符合SPGD 算 法中单路随机序列伯努利分布的要求。但使用M 序列作为SPGD 算法中多路随机序列在实 现上存在难点:算法要求多路伪随机序列,用多个不同的LFSR 结构去生成多路的伪随机 序列,需要耗费大量的硬件资源,并且构造多路不同的LFSR 结构需耗费巨大的工作量。
Gold 序列优点在于只由两个M 序列构造,能够节省资源;并且改变两个M 序列模二 和的相对位置即可构成多个Gold 序列,从而满足SPGD 算法中多路伪随机序列的要求。 但在实际工程中如何方便改变两个M 序列的相对位置以产生多路的Gold 序列亦有难度。 同时,Gold 序列亦存在非平衡性问题,不完符合伯努利分布。
国外最早使用模拟超大规模集成电路(Analog VLSI)做出SPGD 控制算法的Vorontsov 等人设计的随机数发生器,其本质也是LFSR 结构,使用了抽头的方法从而可以用一个 LFSR 结构同时产生19 路的伪随机序列[8],[1]。这种方法的缺陷是如果伪随机序列的路数序 列超过19 路后,则用这个电路结构产生的各路伪随机数之间不是完全相互独立的。
4 连续抽样生成多路伪随机序列的方法
通过以上对M 序列,Gold 序列的分析,结合M 序列易于硬件实现,Gold 序列可生成 多路序列的优点,以及基于时间抽样的思想,设计了如图1 所示硬件结构的68 路伪随机 Gold 序列发生器。
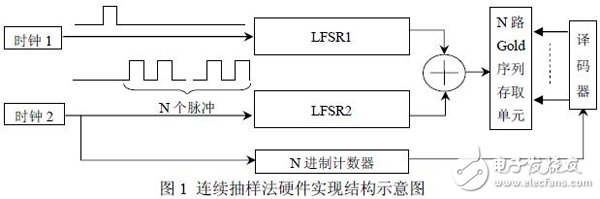
图中所示结构包括两个时钟,两个相同的线性反馈移位寄存器,N 进制计数器,以及N 路伪随机序列的存取单元。两个时钟有特殊的关系,即时钟1 是时钟2 的N 分频。N 进 制计数器的输出作为N 路伪随机序列存取单元的存储地址。存取单元及地址译码器可视为 一个整体,在实现时使用深度为N,宽度为1bit 的双端口RAM 代替(一个端口存数据, 另一个端口取数据)。此外,图中的“+”表示模二和。结构中的N 值,为本原抽样数, 即使用N 对M 序列抽样后,可得到另一同周期的M 序列。
上述结构产生多路Gold 序列的原理如下:

⑤ 将这 N 个不同相位的M2 序列与M1 序列模二和,生成N 个不同的Gold 序列。 该方法需要选定两个可构成Gold 序列的理想M 序列对,之后将能够从一个M 序列抽 样出另一M 序列的本原抽样数N 预先计算出来。由于是预先计算,不需在硬件内实现, 不占用硬件资源。因此该方法占用的资源较少,同时结构化的设计也适合于用硬件描述语 言进行设计。
5 实验及结果分析
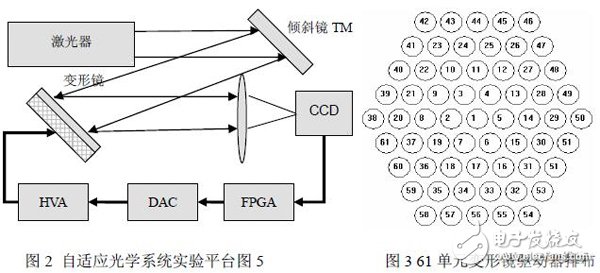
为验证上述伪随机序列生成方法的可行性,在FPGA 内对上述结构进行了硬件设计, 并搭建了基于SPGD 控制算法的自适应光学系统平台。自适应光学系统实验平台的结构如 下图3 所示,主要由激光器和扩束系统、倾斜镜TM、变形镜DM、CCD 相机、基于FPGA 的SPGD 算法控制处理器、数字到模拟转换器DAC 和高压放大器HVA 等组成。光源从激 光器发出后经TM 和DM 反射至CCD 相机,相机将图像数据传输给FPGA 板进行算法迭 代,再输出电压至数模转换,最后经高压放大后控制61 单元的变形镜DM(驱动器的排布 见图(3)和倾斜镜TM,完成闭环控制。
连续抽样法结构的主要参数: LFSR1 和LFSR2 对应的本原多项式为:
本原抽样数N 为68。该设计可产生68路,周期为1023 的Gold 序列。该参数设计主要以实验为主,本原多项式1F (x)的选取原则是反馈少,实现简单。本原抽样数要比61 稍大,保证能产生足够多的Gold 序列,如果过大亦会造成资源的浪费。
SPGD 算法包括伪随机序列发生器都在Xilinx 公司的VII3000 FPGA 内实现。通过 ChipScope 在线逻辑分析仪记录68 路Gold 序列,经计算验证这68 路Gold 满足相互独立 的要求。针对Gold 序列的非平衡性问题,根据序列的周期性及对偶性,实验运用了一个简 单的方法加以解决:将偶数周期的两个样本值互相交换,即应该输出1 时输出0,应该输 出0 时输出1。因此每两个周期内的两个样本值出现的概率各为0.5,只要序列发生的时间 足够长,长期统计平均,其概率亦各为0.5。因此通过实验验证表明连续抽样方法能够满足 自适应光学SPGD 算法的要求。
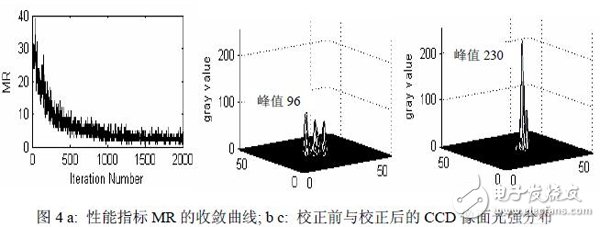
自适应光学系统实验方面,以均值半径作为本实验中SPGD 算法的性能指标[4],向极 小的方向进行梯度搜索,性能指标的收敛曲线如图4(a)所示。在迭代1000 次后,曲线就已 接近极小值。图4(b)和7(c)是进行校正前后,CCD 相机中获取的远场光斑的光强分布图。 校正前的峰值为96,校正后的峰值为230,校正后的远场光斑接近艾里斑,结果说明使用 SPGD 算法对静态的波前畸变达到了良好的效果,同时也验证了本方法所产生的伪随机序 列能够在实际的SPGD 控制算法中正常工作。
6 结论
利用FPGA硬件电路生成了61单元自适应光学系统SPGD控制算法要求的68路伪随机序 列。开展了基于SPGD控制算法自适应光学系统实验,系统能够实时闭环,结果表明了该方 法的实用性。同时,该方法除了满足自适应光学系统SPGD控制算法的专用性外,也为生成 大量的、任意多路的伪随机序列提供了一种通用的方法,在信号处理、信号加密等工程领域 也具有一定的实际意义。
本文作者创新点:针对自适应光学系统的SPGD 控制算法对伪随机序列的要求,分析 了两种适合于硬件实现的伪随机序列――M 序列及Gold 序列的特点,及直接用于SPGD 控制算法存在的问题。在M 序列抽样方法的基础上,提出了一种连续抽样生成多路Gold 序列的方法。该方法在对时间未要求的基础上,以时间来换取空间资源,减少了空间资源 的占用,只需要两个LFSR 结构,解决了生成大量LFSR 结构的工作量问题,方便地实现 了SPGD 控制算法要求的多路、独立伪随机序列的生成,并提出了解决了Gold 序列非平 衡性问题的方法。
-
基于FPGA的伪随机序列有哪些应用?2021-05-08 1552
-
伪随机系列及编码.ppt2008-10-22 785
-
伪随机数发生器的FPGA实现与研究2009-07-22 564
-
Galileo系统伪随机序列生成及其FPGA实现2009-09-01 862
-
一种混沌伪随机序列发生器的FPGA实现2010-10-20 541
-
伪随机序列及PLD实现在程序和系统加密中的应用2006-05-26 994
-
伪随机位序列发生器2009-09-25 1259
-
FPGA的伪随机序列发生器设计2010-04-02 3745
-
基于TDERCS伪随机序列发生器的FPGA设计与实现2011-11-01 543
-
基于Altera的DSP Builder工具箱的伪随机序列产生器设计方法2017-10-30 1152
-
基于多维伪随机序列的AMS算法2017-12-09 1425
-
基于SPGD控制算法自适应光学系统的伪随机序列的设计与要求2019-07-24 3737
-
基于伪随机序列的噪音干扰FPGA实现2019-11-13 2943
-
如何使用FPGA实现伪随机数发生器2021-02-05 1274
-
高压放大器驱动:基于FPGA的SPGD自适应光学控制平台的探索2025-10-11 671
全部0条评论

快来发表一下你的评论吧 !

