信号处理的复频域分析方法推荐

连续时间系统的复频域分析

音频提纲：（文字简略而枯燥，语音才更加详细生动哦）

连续时间系统的复频域分析可以总结为如下三个方面的内容：

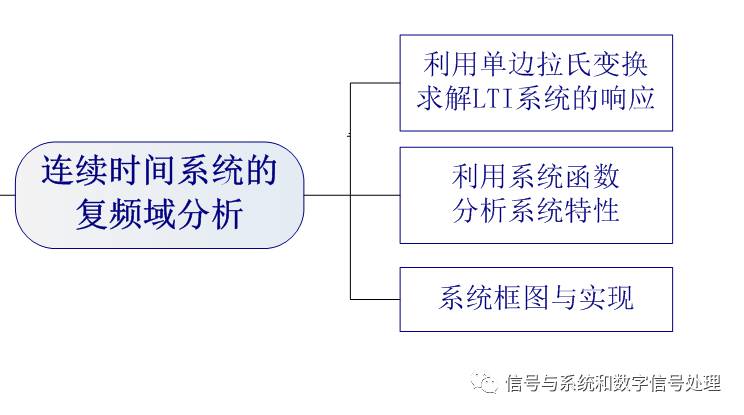
图1

一、利用单边拉氏变换求解LTI系统的响应

1、微分方程的求解

描述连续时间LTI的是常系数的线性微分方程，也就是，由y(t)以及y(t)的各阶导数和x(t)以及x(t)的各阶导数，乘上相应的系数（常数），加加减减组合成的等式。这个时候，拉氏变换的时域微分特性就大有用武之地了。

方程两边取单边LT，利用LT微分性质，就将时域的微分方程，转变成了s域的代数方程（由X(s)、Y(s)以及系统的初始状态y(0-)、y’(0-)......组成），这样，做一个简单的代数运算，就可以求出Y(s)，再求反变换就得到y(t)，这个y(t)是全响应。

图2

    如果要分别求解零输入响应和零状态响应，也很容易。要在求解过程中就分开，看下题，把X(s)放在一堆，初始状态y(0-)、y’(0-)......等等放在一堆，那前者就是零状态响应的拉氏变换，后者就是零输入响应的拉氏变换。

图3

2、电路系统的求解

当然可以先列出电路系统的微分方程，然后利用s域求解方法求解之。但更简便的方法是，利用电阻、电容、电感的复频域等效模型替换，将电路转换为复频域的等效电路，直接列出代数方程。

下图4是电阻、电容和电感的时域及复频域的等效模型。

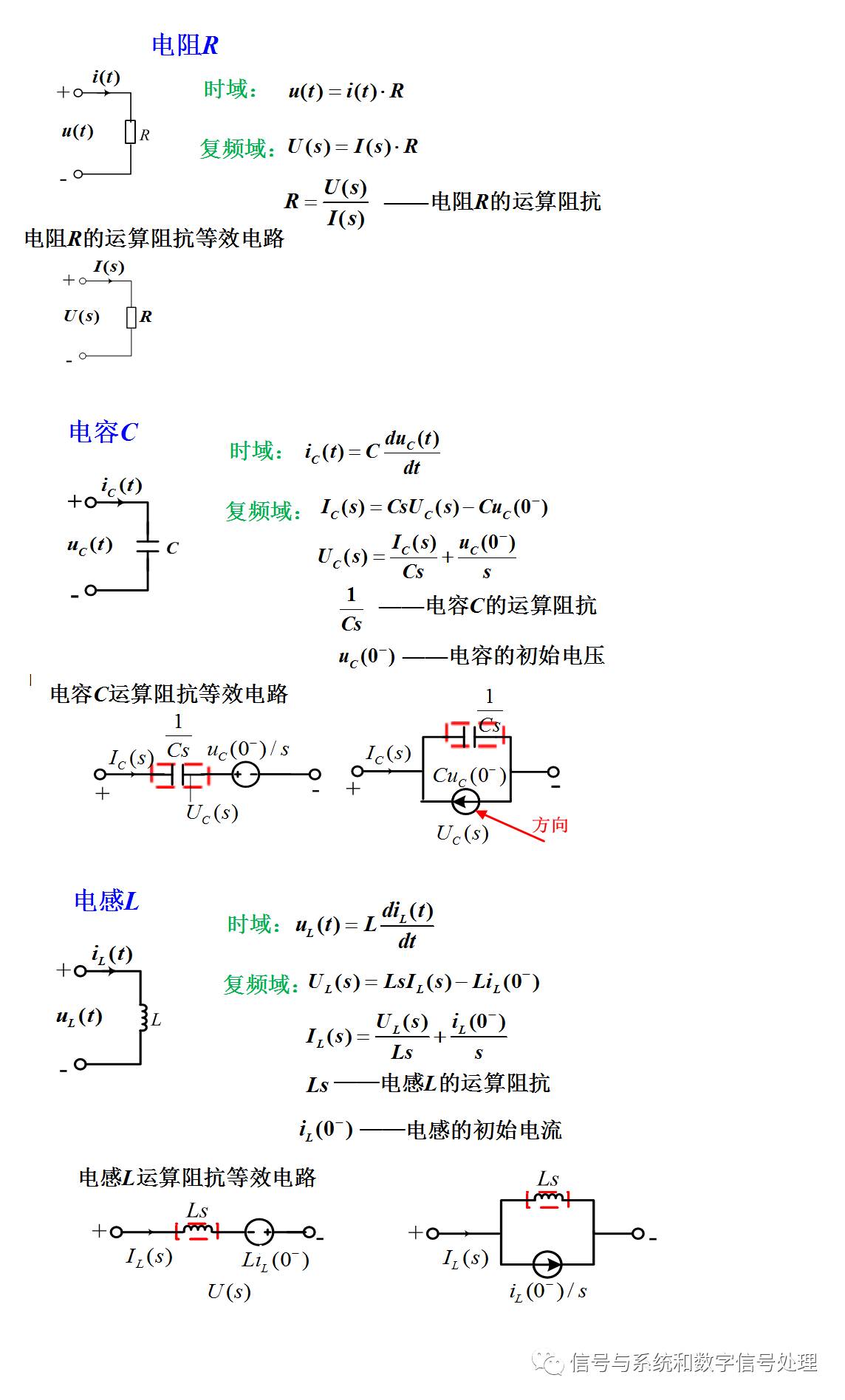
图4

这样，将电路系统转换成s域的等效模型之后，利用KVL或KCL列出方程（这个就是代数方程了），求出Y(s)，再求拉氏反变换即可得出y(t)。

二、利用系统函数分析系统特性

1、系统函数

系统函数H(s)是谁？

H(s)与h(t)的关系：是单位冲激响应h(t)的拉氏变换；

H(s)与输入/输出的关系：是Y(s)/X(s)；

H(s)与H(jw)的关系：H(jw)=H(s)|s=jw

H(s)与微分方程的关系：

H(s)与极零点图的关系：

H(s)与系统框图、流图的关系：

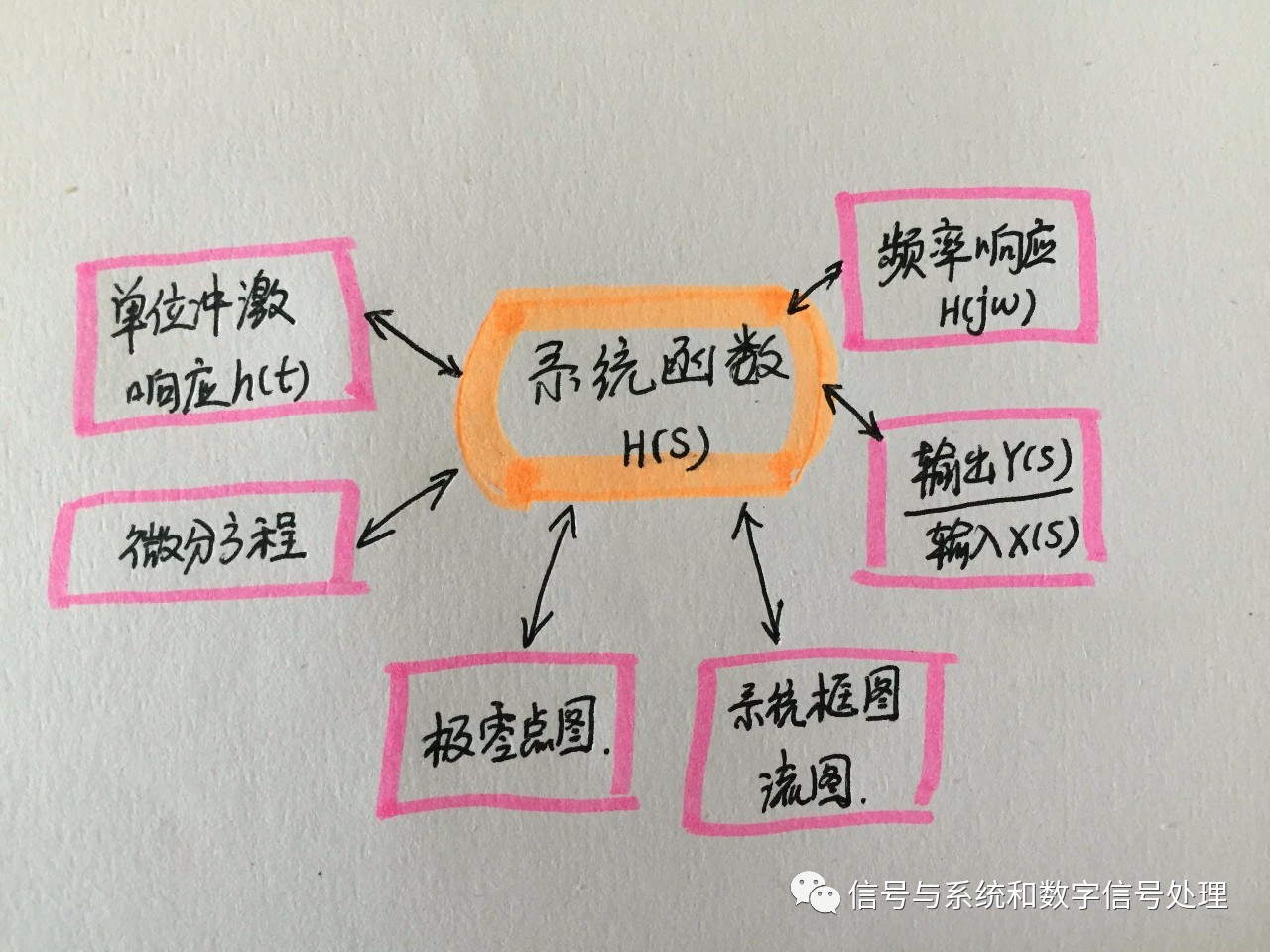
图5

2、稳定性分析

定义：输入有限，则输出一定有限（BIBO）

从时域上看：h(t)满足绝对可积

从复频域上看：

    收敛域：包含虚轴

    极点位置：对于因果系统，所有极点均位于左半平面

劳斯——霍尔维茨准则（但是需要注意，只适用于判断连续时间因果系统的稳定性，而且必须计算到n+2行才有意义）

3、系统函数极零点对滤波器特性的影响

系统的幅频特性=各零点矢量长度之积/各极点矢量长度之积

系统的相频特性=各零点矢量相角之和 - 各极点矢量相角之和

极点对幅频特性的影响——极点增强增益。

  极点对频率选择性的影响是：使得w0处的增益增强。

  随着极点愈靠近虚轴（a减小），增强效果愈明显。如果是高阶极点，增强效果也愈明显。

  共轭极点的存在并不会显著改变w0附近的频率选择特性。

零点对幅频特性的影响——零点抵消增益。

  零点对频率选择性的影响是：使得w0处的增益减小。

  随着零点愈靠近虚轴（a减小），减弱的效果愈明显。当零点在虚轴上时，使w0处增益为零。

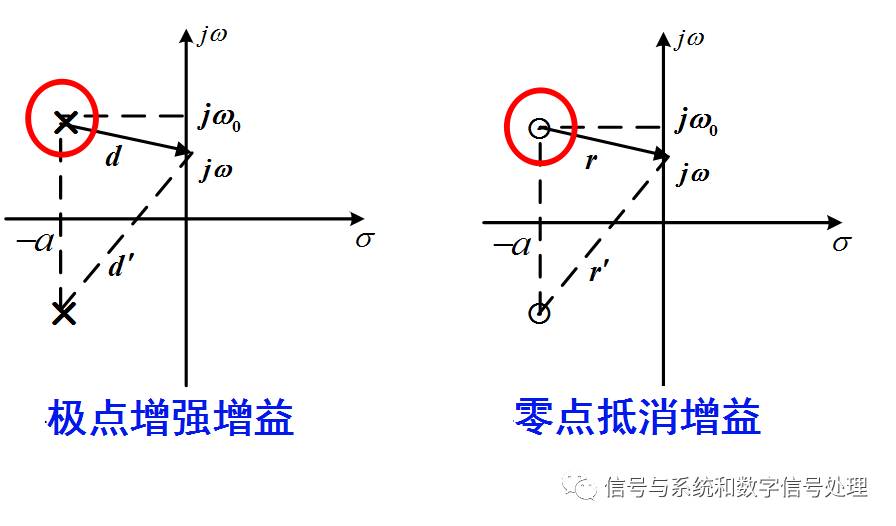
图6

下面给一个典型了例题，根据极零点图判断系统的滤波特性。

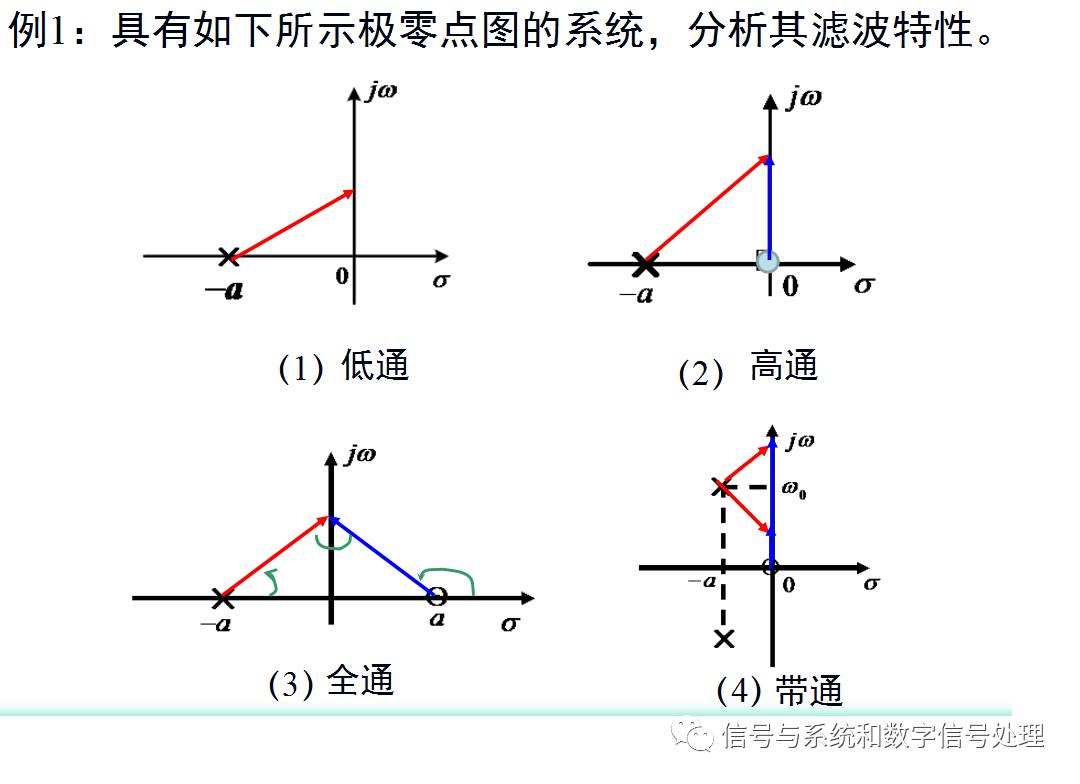
图7

三、系统框图与实现

    

梅森公式是桥梁，可以很方便地在系统函数和流图或框图之间转换。在自动控制、数字信号处理等课程中也有应用。因为内容比较简单，这里不再赘述。