什么是卷积_卷积的意义

　　卷积的定义

　　卷积是两个变量在某范围内相乘后求和的结果。

　　如果卷积的变量是序列x（n）和h（n），则卷积的结果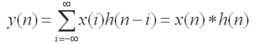，其中星号*表示卷积。

　　当时序n=0时，序列h（-i）是h（i）的时序i取反的结果；时序取反使得h（i）以纵轴为中心翻转180度，所以这种相乘后求和的计算法称为卷积和，简称卷积。

　　另外，n是使h（-i）位移的量，不同的n对应不同的卷积结果。如果卷积的变量是函数x（t）和h（t），则卷积的计算变为，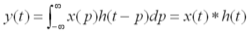

　　其中p是积分变量，积分也是求和，t是使函数h（-p）位移的量，星号*表示卷积。

　　卷积的定理

　　卷积定理指出，函数卷积的傅里叶变换是函数傅里叶变换的乘积。即，一个域中的卷积相当于另一个域中的乘积，例如时域中的卷积就对应于频域中的乘积。

　　F（g（x）*f（x））=F（g（x））F（f（x））

　　其中F表示的是傅里叶变换。

　　这一定理对拉普拉斯变换、双边拉普拉斯变换、Z变换、Mellin变换和Hartley变换（参见Mellininversiontheorem）等各种傅里叶变换的变体同样成立。在调和分析中还可以推广到在局部紧致的阿贝尔群上定义的傅里叶变换。

　　利用卷积定理可以简化卷积的运算量。对于长度为n的序列，按照卷积的定义进行计算，需要做2n-1组对位乘法，其计算复杂度为；而利用傅里叶变换将序列变换到频域上后，只需要一组对位乘法，利用傅里叶变换的快速算法之后，总的计算复杂度为。这一结果可以在快速乘法计算中得到应用。

　　卷积的意义

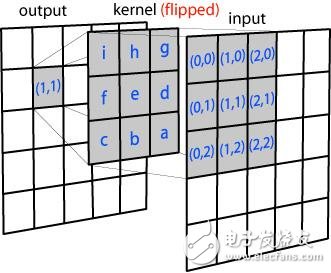
　　用一个模板和一幅图像进行卷积，对于图像上的一个点，让模板的原点和该点重合，然后模板上的点和图像上对应的点相乘，然后各点的积相加，就得到了该点的卷积值。对图像上的每个点都这样处理。由于大多数模板都是对称的，所以模板不旋转。卷积是一种积分运算，用来求两个曲线重叠区域面积。可以看作加权求和，可以用来消除噪声、特征增强。

　　把一个点的像素值用它周围的点的像素值的加权平均代替。

　　加权叠加：对于线性时不变系统，如果知道该系统的单位响应，那么将单位响应和输入信号求卷积，就相当于把输入信号的各个时间点的单位响应加权叠加，就直接得到了输出信号。

　　通俗的说：

　　在输入信号的每个位置，叠加一个单位响应，就得到了输出信号。

　　这正是单位响应是如此重要的原因。

　　在输入信号的每个位置，叠加一个单位响应，就得到了输出信号。

　　这正是单位响应是如此重要的原因。

　　在输入信号的每个位置，叠加一个单位响应，就得到了输出信号。

　　这正是单位响应是如此重要的原因。

　　卷积的应用

　　卷积是一种线性运算，图像处理中常见的mask运算都是卷积，广泛应用于图像滤波。

　　卷积关系最重要的一种情况，就是在信号与线性系统或数字信号处理中的卷积定理。利用该定理，可以将时间域或空间域中的卷积运算等价为频率域的相乘运算，从而利用FFT等快速算法，实现有效的计算，节省运算代价。

　　在工程和数学上的应用

　　统计学中，加权的滑动平均是一种卷积。概率论中，两个统计独立变量X与Y的和的概率密度函数是X与Y的概率密度函数的卷积。声学中，回声可以用源声与一个反映各种反射效应的函数的卷积表示。电子工程与信号处理中，任一个线性系统的输出都可以通过将输入信号与系统函数（系统的冲激响应）做卷积获得。物理学中，任何一个线性系统（符合叠加原理）都存在卷积。

　　介绍一个实际的概率学应用例子。假设需求到位时间的到达率为poisson（λ）分布，需求的大小的分布函数为D（。），则单位时间的需求量的分布函数为F（x）：

　　其中D（k）（x）为k阶卷积。

　　卷积是一种线性运算，图像处理中常见的mask运算都是卷积，广泛应用于图像滤波。castlman的书对卷积讲得很详细。

　　高斯变换就是用高斯函数对图像进行卷积。高斯算子可以直接从离散高斯函数得到：

　　for（i=0;i《N;i++）

　　{

　　for（j=0;j《N;j++）

　　{

　　g［i*N+j］=exp（-（（i-（N-1）/2）^2+（j-（N-1）/2）^2））/（2*delta^2））;

　　sum+=g［i*N+j］;

　　}

　　}

　　再除以sum得到归一化算子

　　N是滤波器的大小，delta自选

　　首先，在提到卷积之前，必须提到卷积出现的背景。卷积是在信号与线性系统的基础上或背景中出现的，脱离这个背景单独谈卷积是没有任何意义的，除了那个所谓褶反公式上的数学意义和积分（或求和，离散情况下）。

　　信号与线性系统，讨论的就是信号经过一个线性系统以后发生的变化（就是输入输出和所经过的所谓系统，这三者之间的数学关系）。所谓线性系统的含义，就是，这个所谓的系统，带来的输出信号与输入信号的数学关系式之间是线性的运算关系。

　　因此，实际上，都是要根据我们需要待处理的信号形式，来设计所谓的系统传递函数，那么这个系统的传递函数和输入信号，在数学上的形式就是所谓的卷积关系。

　　卷积关系最重要的一种情况，就是在信号与线性系统或数字信号处理中的卷积定理。利用该定理，可以将时间域或空间域中的卷积运算等价为频率域的相乘运算，从而利用FFT等快速算法，实现有效的计算，节省运算代价。

　　在地震中的应用

　　地震勘探中，在地表激发点激发的地震子波（seismicwavelet）向地下传播，当遇到地下波阻抗界面时，一部分能量就会作为反射地震波向上反射回地表，被地面的传感器接收，随着地震波不断向下传播、反射、接收，就会记录一系列时间延迟的地震波（大地滤波后的地震子波），称为地震记录。这一过程或地震记录可以用数学模型描述。如果假设地下介质为古皮奥（Goupilaud）的水平层状介质模型，子波为雷克（Ricker）子波，地震记录可以看作是由震源子波与地下反射率函数、多次反射、仪器等诸多因素的相褶积的过程，令x（t），w（t）和n（t）分别表示地震记录，地震子波及噪声，褶积过程数学模型描述为：长期以来，褶积模型广泛用于描述地震信号。顾名思义，反褶积就是褶积的逆过程，从地震记录x（t）中恢复出反射率函数r（t）。