

欧拉公式与三角函数_欧拉公式推导三角函数
电子常识
描述
欧拉公式与三角函数
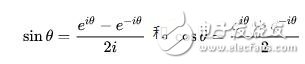
根据欧拉公式 1 ,可以轻易推出:
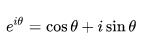
三角函数定义域被扩大到了复数域。我们把复数当作向量来看待,复数的实部是 X 方向,虚部是Y 方向,很容易观察出其几何意义。
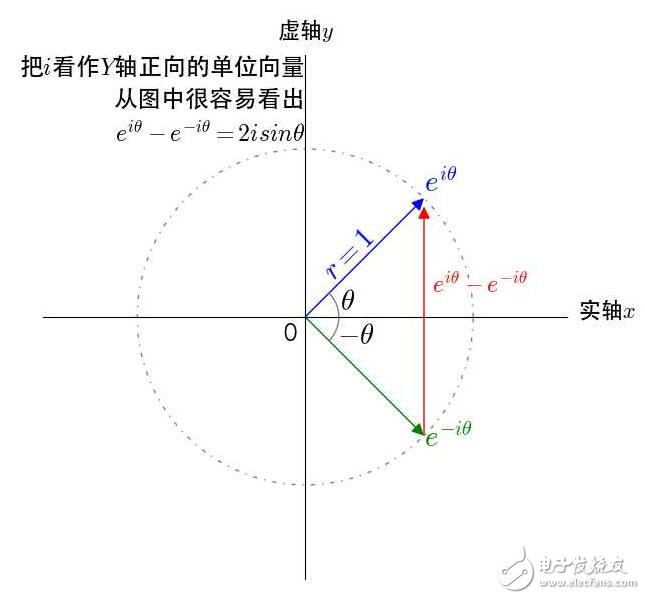
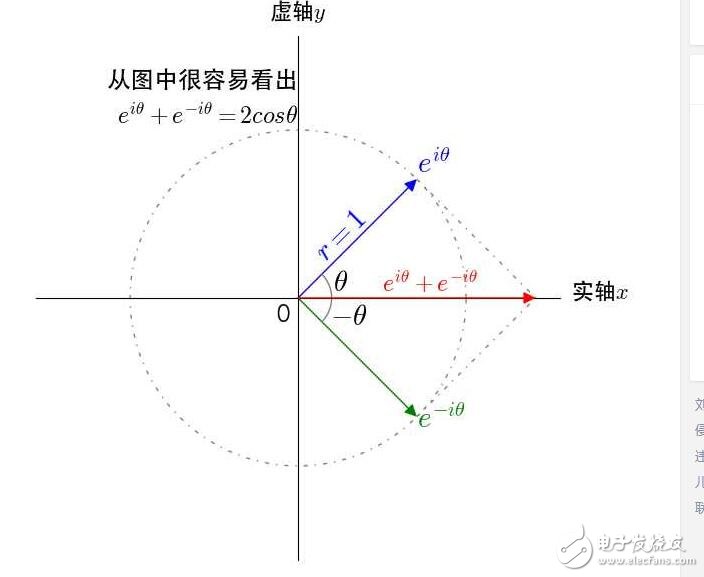
欧拉公式推导三角函数
将三角函数的定义域扩大到复数,建立了三角函数和指数函数的关系,它在复变函数论里占有非常重要的地位,并且有着广泛而重要的应用利用欧拉公式易得:
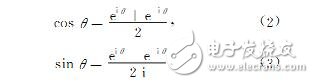
因此,欧拉公式使指数函数和三角函数在复数域中实现了相互转化.近年来,欧拉公式已被广泛应用到初等数学和高等数学。本文将利用欧拉公式导出部分三角函数公式。
1、三角函数大降幂
高次幂的正余弦函数在计算上给我们带来诸多不便,利用欧拉公式可把高次幂的正余弦函数表示为一次幂函数的代数和,从而简化计算。
1.1 余弦大降幂由式(2)易得:

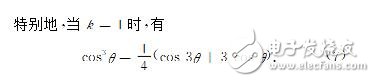
1.2正弦大降幂由式(3)及式(2)易得:

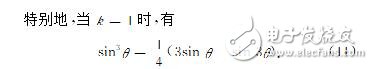
以上所得到的降幂公式(4)(6)(8)(10)皆与数学手册[8]中给出的降幂公式完全一致
2 、导出三角函数多倍角公式
根据欧拉公式(1),一方面有:
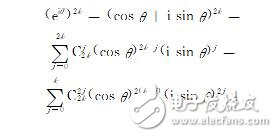


以上所得到的多倍角公式(14)(15)和(20)(21)也与数学手册[8]中完全一致。
3、导出和差化积公式文[3]利用欧拉公式导出了两角和(差)的正、余弦公式
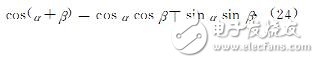
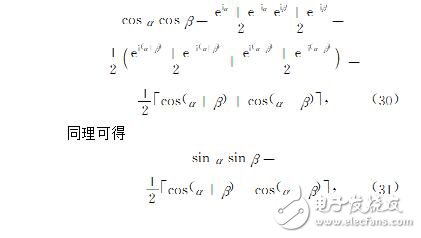
4、导出积化和差公式利用欧拉公式易得
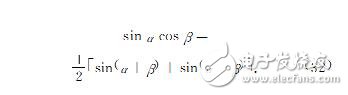
5、结束语
在数学历史上有很多公式都是欧拉发现的,它们都叫做欧拉公式,且分散在各个数学分支之中,复变函数论里的欧拉公式是最著名的欧拉公式之一.三角函数公式众多,类型纷繁、灵活,这给解决三角变换问题带来了诸多不便,本文通过欧拉公式来推导得出的结论,不仅可以使计算方便,也有很多理论上的意义.
- 相关推荐
- 热点推荐
- 欧拉公式
-
RX系列三角函数单元(TFU)的使用介绍2023-12-04 4025
-
马达控制上必要的知识 三角函数2025-03-18 3214
-
三角函数的查表法2025-11-19 45
-
ARM7如何实现三角函数2013-11-12 3115
-
labview的三角函数pi在哪2016-03-23 14244
-
电磁波为什么要用三角函数表示?2021-10-25 3262
-
labview中的三角函数问题2022-04-09 9855
-
基于DSP的三角函数快速计算2010-04-07 704
-
反三角函数arcranx运算电路2009-04-09 3040
-
基于三角函数搜索因子的混合蛙跳算法2017-11-24 824
-
欧拉公式怎么写_欧拉公式的意义2017-11-28 43143
-
如何使用Cordic算法C语言实现三角函数的计算2019-04-25 3062
-
如何使用DSP汇编语言实现高精度的三角函数2020-08-28 3139
-
AD639:通用三角函数转换器废弃数据表2021-05-17 1482
-
TI Arm内核三角函数的优化2024-09-11 414
全部0条评论

快来发表一下你的评论吧 !

