一种基于Diakoptics的计算微波电路的设计和实现

一、引 言

随着计算机技术的进步，时域有限差分法（FiniteDifference TimeDomain）是一种求解电磁问题的数值计算技术，由K.S.Yee于1966年提出。他的基本思想是根据时域麦克斯韦方程的场分量微分式，用差分替代微分式，进行各场分量的迭代，但是这种方法随着频率升高，计算网格将显著增加，PC机的性能将很难满足需要，而且单纯依靠计算机性能的提高也是不实际的。例如，在分析波导膜片滤波器时，为正确模拟全部膜片的几何结构，FDTD栅网的网格尺寸选得非常小，从而导致描述整个波导滤波器的网格数量非常大。由于每两个膜片之间都是均匀波导传输线，使用与膜片相同的栅网显然是不必要的。人们曾使用非均匀FDTD栅网的办法解决这个问题，当栅网的大小相差比较大时，不但收敛性不易控制，而且仍无法确保节省计算时间。将Diakoptics思想运用于微波电路的全波分析，通过将电路分割为若干独立的部分，根据每部分的具体结构采用不同的网格，独立地对各个部分进行全波时域分析，由于每部分的网格是均匀的，因而容易保证算法的收敛性。

二、Diakoptics的概念

Diakoptics的概念来源于网络理论。其定义为：将一个网络分解为若干子网络，对每个子网络的冲击响应单独求解，最后通过一定的连接条件，由诸子网络的冲击响应求出网络总的响应。连接条件按形式不同可分为串行连接及并行连接。串行连接是依照一定的顺序由网络的一端向另一端单向连接，见图1,其优点是简单，但最大的问题是当其中一个子网络的冲击响应改变时，将对其后的网络产生影响。并行连接可克服这个缺点。并行连接可在任意两个相邻的子网络间进行，且若干并行连接可同时独立进行，并行时域Diakoptics假设子网络为M+N端口网络，其中M个端口和前一级子网络相连，N个端口和后一级子网络相连。子网络的离散格林函数为g（i,j,n′）即j（j=1,M+N）端口t=0时刻的激励，在i（i=1,M+N）端口t=n′时刻的冲击响应。

研究微波电路问题时，若微波电路可以被等效为一个线性网络的话，则可以设想描述微波电路特性的格林函数可对应于电路理论中的冲击响应函数。从电磁场理论角度看，时域格林函数g（r,t;r0,t0）为位于r0点的点源t0时刻施加的单位冲击信号在观察点r及t时刻的场，且满足方程

两个微波子电路连接时，其连接参考面上存在着复杂的耦合关系，这种耦合关系可以用电磁波在存在两个不连续界面的媒质中反射和透射现象来形象描述，如图1所示。那么如何将Diakoptics算法应用于微波电路特性分析中呢？在介绍这一点之前，本文首先简要介绍Diakoptics算法的数学描述。

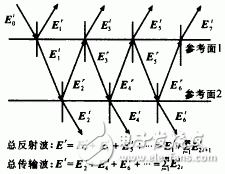
图1　媒质中反射和透射现象可以用来形象描述两个微波子电路间的耦合关系

三、Diakoptics算法的数学描述

以两个二端口网络的串、并行连接给出Diakoptics算法的数学描述。图2假设两个子电路的反射及透射波的冲击响应函数分别为：gr1（t），gr2（t），gt1（t），gt2（t）和hr1（t），hr2（t），ht1（t），ht2（t），上标"r"表示反射波，"t" 表示传输波，下标1表示从输入参考面对电路作激励，下标2表示从输出参考面对电路作激励。设f为两个子电路连接后电路的冲击响应函数。使用串行算法，从f 网络输入参考面看入的冲击响应为：

fr1（t）=gr1（t）+gt2（t）*hr1（t）*gt1（t）+gt2（t）*hr1（t）

*gr2（t）*hr1（t）*gt1（t）+…+gt2（t）*（hr1（t）

*gr2（t））n*hr1（t）*gt1（t）+…； （2）

使用并行算法，从f电路的输入端口看入的冲击响应函数fr1（t），ft2（t）以及从f电路的输出端口看入的冲击响应函数fr2（t），ft1（t）分别为：

fr1（t）=gr1（t）+gt2（t）*hr1（t）*gt1（t）+gt2（t）*hr1（t）

*gr2（t）*hr1（t）*gt1（t）+…+gt2（t）*（hr1（t）

*gr2（t））n*hr1（t）*gt1（t）+…

ft2（t）=gt2（t）*hr2（t）+gt2（t）*hr1（t）*gr2（t）*ht2（t）+…

+gr2（t）*（hr1（t）*gr2（t））n*hr2（t）+… （3）

fr2（t）=hr2（t）+ht1（t）*gr2（t）*ht2（t）+ht1（t）*gr2（t）

*hr1（t）*gt2（t）*ht2（t）+…+ht1（t）*（gr2（t）

*hr1（t））n*gr2（t）*ht2（t）+…

ft1（t）=ht1（t）*gt1（t）+ht1（t）*gr2（t）*hr1（t）*gt1（t）+…

+ht1（t）*（gr2（t）*hr1（t））n*gr1（t）+…

其中，*代表时域卷积，上下标的含义不变。

 

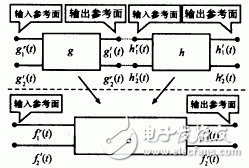
图2　可说明Diakoptics算法的两个子电路连接示意图

多端口子电路连接时，上述算法依然成立，只是式中各冲击函数应换为相应的子矩阵。例如设g网络为输入端有M个、输出端有N个端口的M+N端口网络，h网络为输入端有N个、输出端有L个端口的N+L端口网络（g与h相邻面的端口数目应相同），g网络输入参考面处的反射、传输子矩阵分别为：

 

和

式中下标代表参考面，i←j的意思为：i为响应所在参考面，j为激励所在参考面；上标代表端口，m←n的意思为：n为输入端口，m为输出端口。同理，g网络输出参考面处的反射、传输子矩阵分别为：

和

h网络相应子矩阵可用同样方法求得。连接后网络的冲击响应函数[f]为：

[fr1（t）]=[gr1（t）]+[gt2（t）]*[hr1（t）]*[gt1（t）]+[gt2（t）]

*[hr1（t）]*[gr2（t）]*[hr1（t）]*[gt1（t）]+…

[ft2（t）]=[gt2（t）]*[ht2（t）]+[gt2（t）]*[hr1（t）]*[gr2（t）]*[ht2（t）]+…

[fr2（t）]=[hr2（t）]+[ht1（t）]*[gr2（t）]*[ht2（t）]+[ht1（t）]

*[gr2（t）]*[hr1（t）]*[gr2（t）]*[ht2（t）]+…

[ft1（t）]=[ht1（t）]*[gt1（t）]+[ht1（t）]*[gr2（t）]*[hr1（t）]*[gt1（t）]+… （4）

其中[fr1（t）]、[ft1（t）]、[fr2（t）]和[ft2（t）]分别为M×M、L×M、L×L和M×L阶子矩阵。下面以[gt2（t）]*[ht2（t）]为例说明如何计算矩阵卷积，并以[gt2（t）]*[ht2（t）]的第一个元素为例，说明其物理意义：

g1←11←2*h1←11←2:h子网络输出参考面上第一个端口的输入通过gh连接面第1个端口的耦合在g子网络输入参考面上端口1产生的输出；g1←21←2*h2←11←2:h子网络输出参考面上第一个端口的输入通过gh交界面第2个端口的耦合在g子网络输入参考面上端口1产生的输出；g1←N1←2*hN←11←2:h子网络输出参考面上第一个端口的输入通过gh交界面第N个端口的耦合，在g子网络输入参考面上端口1产生的输出；所以[gt2（t）]*[ht2（t）]的第一个元素描述了h网络输出参考面上第一个端口上的输入耦合到g网络输入参考面第一个端口的输出。