Curvelet变换在图像处理中的应用综述

　　近年来，Donoho等人提出的Curvelet变换引起了有关研究人员的密切关注尤其在图像处理领域，它被认为即将成为一项非常有用的新技术Curvelet变换是在研究小波变换的基础上发展起来的，它克服了小波变换在应用中的不足，显示出了许多独到之处众所周知，在小波变换出现的近20年间，它在信号处理中的应用得到了很大的发展，其地位也日益重要根本上讲，这得益于小波变换能够高效地对一维分段连续信号进行分析对于二维图像处理，常用的二维小波是一维小波的张量积，采用分离的变换核先对图像做水平方向的小波变换，然后再进行垂直方向的小波变换，这样的二维小波变换的基是各向同性的（isotropic），变换系数的局部模极大值只能反映出这个小波系数出现的位置是过边缘（acrossedge）的，而无法表达沿边缘（alongedge）的信息，这就使得传统小波变换在处理二维图像时表现出一定的局限性针对小波变换的上述缺点，Donoho等人提出Curvelet变换理论，其各向异性特征非常有利于图像边缘的高效表示这一特点使得Curvelet变换自1999年问世以来得到了相关研究者的高度重视，在图像处理和分析中已经取得了很多研究成果本文将扼要介绍Curvelet变换在图像去噪、图像增强、图像融合、图像恢复等几个方面的应用，结合研究中实现的部分算法进行实验说明，并探讨它的发展趋势及一些有待进一步研究的问题

　　curvelet的性质

　　小波变换是一种具有较强时、频局部分析功能的非平稳信号分析方法成功地应用于信号的特征提取领域，曲波变换作为新一代的多尺度几何分析工具取得了较好的识别效果，它考虑了尺度、位置、角度信息使其在表达图像中的曲线时明显优于小波变换。

　　Curvelet变换各向异性的特点更适合分析图像中的曲线或直线状边缘特征。

　　符合生理学研究指出的“最优”图像表示方法应该具有的三种特征，多分辨、带通、具有方向性。

　　Curvelet变换的基本理论

　　如前所述，小波变换在某些应用中长期受到沿边缘信息表达能力不足的困扰，虽然研究人员提出不少改进方法，但都没有从本质上进行革新为克服这一局限，1998年Cands提出了Ridgelet变换：对图像进行Radon变换，即把图像中的一维奇异性，比如图像中的直线，映射成Radon域的一个点，然后用一维小波进行点奇异性的检测，从而有效地解决了小波变换在处理二维图像时的问题然而，自然图像中的边缘线条以曲线居多，对整幅图像进行单尺度Ridgelet分析并不十分有效，因此需要对图像进行分块，使每个分块中的线条都近似直线，再对每个分块进行Ridgelet变换，这就是多尺度Ridgelet由于多尺度Ridgelet分析冗余度很大，Donoho等人提出了Curvelet变换：首先对图像进行子带分解;然后对不同尺度的子带图像采用不同大小的分块;最后对每个块进行Ridgelet分析每个子块的频率带宽width、长度length近似满足关系width=length2这种频率划分方式使得Curvelet变换具有强烈的各向异性，而且这种各向异性随着尺度的不断缩小呈指数增长研究表明，用有限的系数来逼近一段C2连续的曲线时，Curvelet变换的速度远远快于傅里叶变换和小波变换换言之，对此类曲线而言，Curvelet变换是其最稀疏的表示方法总之，Curvelet结合了Ridgelet变换的各向异性特点和小波变换的多尺度特点，因此它的出现对于二维信号分析具有里程碑式的意义

　　下面简要介绍Curvelets变换的主要步骤

　　

　　

　　

　　上式表明Ridgelet变换是对Radon变换的切片的一维小波分析，其中方向角是固定的，而变量t是小波分析的对象

　　Curvelet变换的数字实现

　　根据上述理论，Starck等人提出了一种Curvelet变换的数字实现算法，其主要步骤为

　　子带分解采用trous小波算法把图像分解到不同的子带

　　分块每一个子带加窗处理，而且每隔一个子带，窗口的宽度增加一倍

　　数字Ridgelet分析对每一个正方块进行Ridgelet变换其中包括二维傅氏变换、直角坐标转换成极坐标、在各角度对应直线上分别作一维傅氏逆变换和一维小波变换等几个中间步骤

　　数字Curvelet逆变换的实现只需将上述步骤逆序进行即可。

　　Curvelet变换的应用

　　由前述的Curvelet变换基本思想及其特性可知，它相对于小波变换的最大特点是具有高度的各向异性，因此具有更强的表达图像中沿边缘信息的能力在图像处理中，边缘往往是最重要的特征，它对于进一步的处理和分析有着至关重要的意义而在实际情况中，图像边缘又常被其他因素削弱，比如为噪声所掩盖，等等在这种环境下，Curvelet变换所表达的沿边缘信息对于恢复图像主要结构的视觉特征的优势是不言而喻的下面主要介绍Curvelet变换在图像去噪、增强、融合、恢复等几个方面的应用方法及其效果

　　利用Curvelet变换抑制图像噪声

　　去除加性噪声

　　传统的图像随机噪声消除或抑制的方法可分为频域滤波方法和空域平滑方法，其缺点是都要损失大量的图像信息目前较新而且有效的去噪方法是小波域滤波但是小波算法用于图像去噪有内在的局限性，因为对图像进行二维小波变换以后，重要边缘上的系数即使在很精细的尺度下也很大，这意味着要重建图像边缘，就必须保留大量的小波系数根据统计原理，数据的精简与其精确性之间有矛盾，即便取二者之间最好的折衷，仍将导致较高的均方误差由于Curvelet变换能用极少的非零系数精确表达图像边缘，因此可以在保证较低的均方误差基础上，达到较理想的图像数据的精简性与精确性的平衡，从而体现出它在噪声环境下优于小波的表达图像的能力

　　基于Curvelet变换的去噪算法概要：对图像进行Curvelet变换，然后对每个子带的变换系数做硬阈值处理，最后进行Curvelet逆变换得到去噪图像在阈值的选取上，是保留较大的系数，舍弃较小的系数，因为根据Curvelet变换理论，较大的Curvelet系数对应于较强的边缘，反之为噪声图1是我们在实验中截取的Lena图像去噪的部分结果，其中图1（a）为高斯噪声污染的原图，图1（b）为非抽样小波去噪结果，图1（c）为Curvelet去噪结果

　　

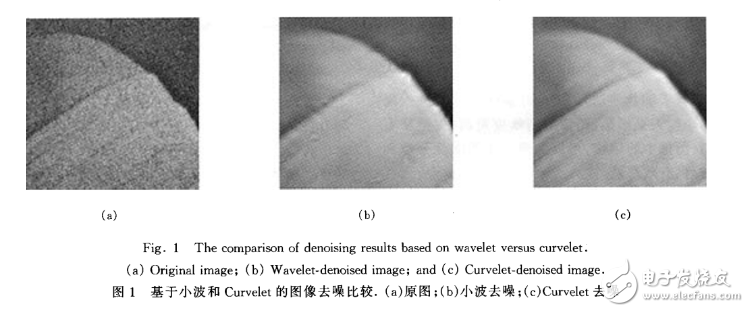
　　通过对几幅内嵌高斯白噪声的标准图像进行实验，结果显示Curvelet算法的峰值信噪比（PSNR）高于多数基于小波的方案，而且Curvelet重建的图像不会产生像小波重建图像的沿边缘的走样（artifact）如抽样小波算法会产生边界扭曲现象并损失大量细节;非抽样小波的边界效果虽然略好，但有时仍忽略了某些脊（ridge），还会显示出一些小尺度的嵌入污点可见即使只是简单的取硬阈值，Curvelet去噪算法的PSNR与较复杂的小波去噪算法相当甚至更高在中等程度或高噪声背景下，Curvelet算法的结果图在视觉上更清晰，特别对于恢复边缘和微弱的线性及曲线结构非常有效

　　上述去噪方案仍有不足，由于采用的Ridgelet变换有环绕（warparound）现象，影响了Ridgelet变换以直线为单位分析图像的性质肖小奎等人的解决方案是对一n*n图像补零至2n*2n个点后再进行离散傅里叶变换，从而避免了进行一维傅里叶反变换时所出现的混迭现象此外，由于Starck等人在去噪时采用了硬阈值，对小波系数的衰减又在频域中进行，所以去噪后的图像中呈现出一定的振铃效应对此，肖小奎等人将频域中小波系数变换到时域中再进行硬阈值去噪，同时改进了Xu等人提出的子带相关去噪法，将其与硬阈值法进行了结合实验证明去除了环绕现象，去噪后的图像PSNR值和视觉效果都有所改进

　　变化后系数矩阵维度的理解

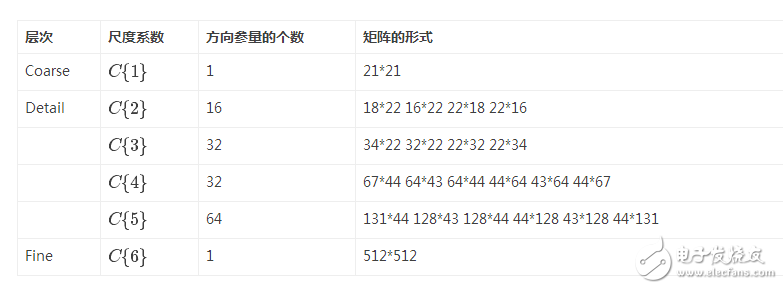
　　下表显示了对图像做C = fdct_wrapping（X，0，2，6，16）;变换后，得到系数C的详细信息，其中原始图片大小为512*512。最内层即Coarse是由低频系数组成的一个矩阵，最外层Fine是高频系数组成的矩阵。

　　

　　尺度数s的影响

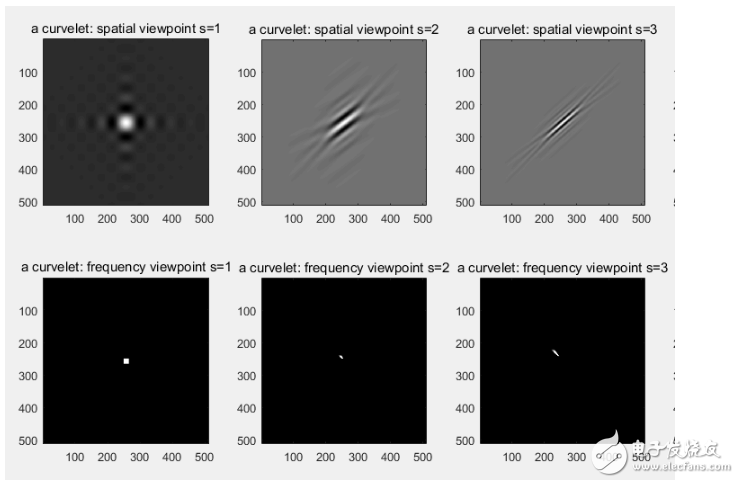
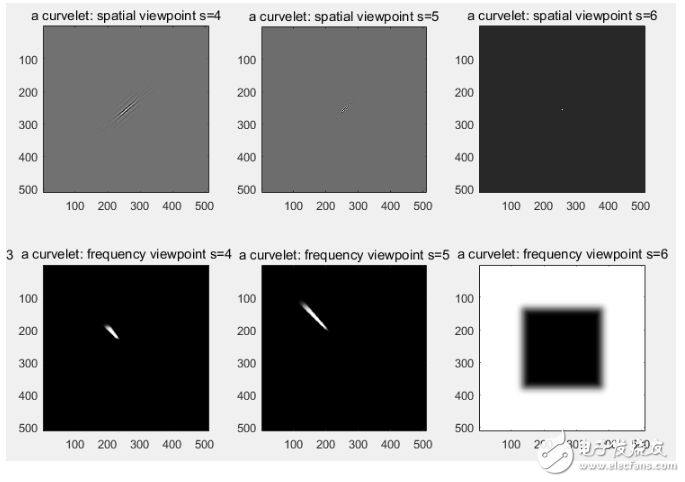
　　下图显示了对图像做C = fdct_wrapping（X，0，2，6，16）;变换后，s=1:6，w=1下的空间域与频域的图像。可以看出：

　　1. 随着s增大，即尺度由最佳尺度变为最粗尺度时，空间域的“针”图形组件变细，而频率域的“针”图像逐渐变粗。这个可以由空间域和频率域具有一定的对称性得知，空间域越“胖”，频率域越“瘦”。

　　2. 尺度s值越大，代表的的越是高频信息。

　　

　　

　　角度数w的影响

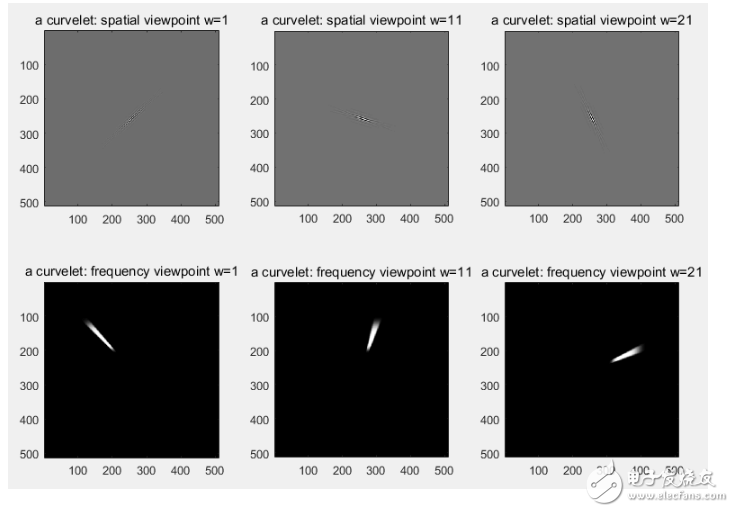
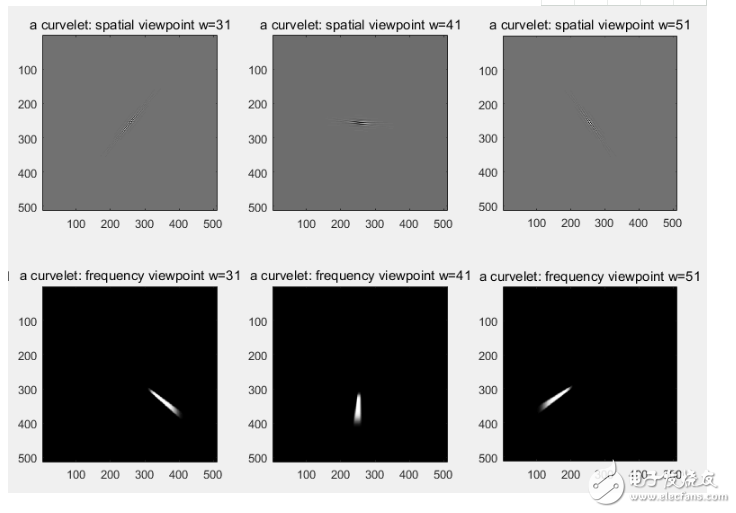
　　下图显示了对图像做C = fdct_wrapping（X，0，2，6，16）;变换后，s=5，w=1:10:60下的空间域与频域的图像。可以看出：

　　w=1时，“楔形”位于左上角位置，随着w增大，“楔形”顺时针转动。由于空间限制，只贴出部分图片。

　　

　　

　　位置a b（其元素值为1）的影响

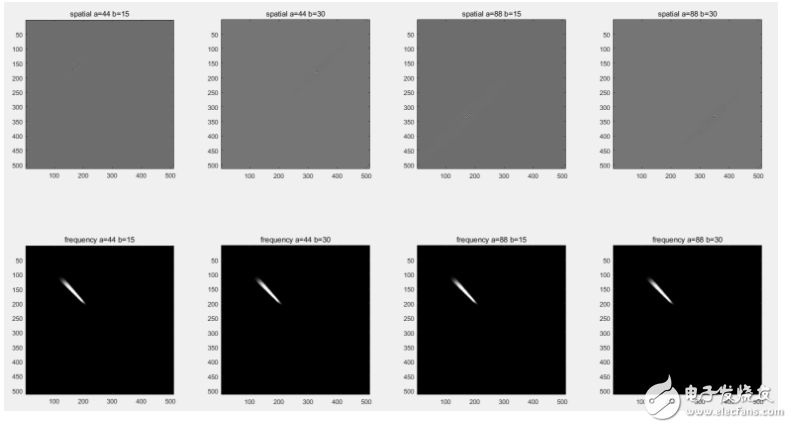
　　下图所示为对原始图像进行C = fdct_wrapping（X，0，2，total_s，16）;，改变C{5}{1}（a，b）=1;，a b取值变化时所对应空间域与频率域的图像，可以看出：

　　a b的改变并不会对频率域图像造成影响，而在空间域上“针”状物体会根据a b的值发生相应的位移。