朴素贝叶斯算法的后延概率最大化的认识与理解

　　朴素贝叶斯法是基于贝叶斯定理与特征条件独立假设的分类方法。最为广泛的两种分类模型是决策树模型（Decision Tree Model）和朴素贝叶斯模型（Naive Bayesian Model，NBM）。

　　和决策树模型相比，朴素贝叶斯分类器（Naive Bayes Classifier，或 NBC）发源于古典数学理论，有着坚实的数学基础，以及稳定的分类效率。同时，NBC模型所需估计的参数很少，对缺失数据不太敏感，算法也比较简单。理论上，NBC模型与其他分类方法相比具有最小的误差率。但是实际上并非总是如此，这是因为NBC模型假设属性之间相互独立，这个假设在实际应用中往往是不成立的，这给NBC模型的正确分类带来了一定影响。

　　模型讲解

　　条件概率分布的参数数量是指数级的，也就是X和Y的组合很多，造成维数灾难，导致实际无法运算。此处，朴素贝叶斯法对它做了条件独立性的假设：

　　

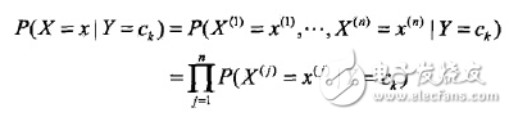
　　也就是各个维度的特征在类确定的情况下都是独立分布的。这一假设简化了计算，也牺牲了一定的分类准确率。基于此假设，以及贝叶斯定理，后验概率为：

　　

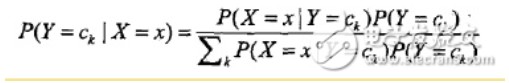
　　分母其实是P（X=x），等同于枚举ck求联合分布的和：∑P（X=x，Y=ck），此联合分布按公式：

　　

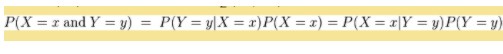
　　拆开，等于上式分母。将独立性假设代入上式，得到：

　　

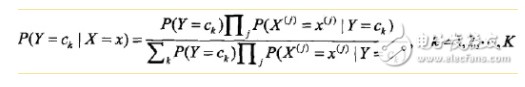
　　朴素贝叶斯分类器可以表示为：

　　

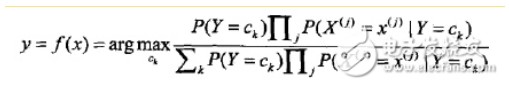
　　也就是给定参数，找一个概率最大的ck出来。注意到上式分母其实就是P（X=x），x给定了就固定了，跟ck一点关系都没有，所以分母可以去掉，得到：

　　

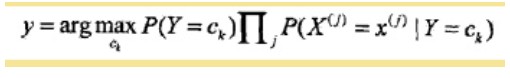
　　后验概率最大化等价于期望风险最小化。如下解释

　　选择0-1损失函数，如下：

　　

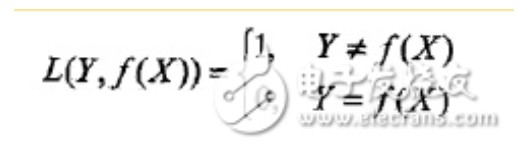
　　f（X）就是分类器的决策函数，损失函数的参数其实是一个联合分布。此时期望风险函数为：

　　

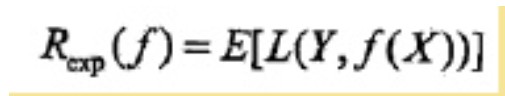
　　上面说过，这是一个联合分布P（X，Y），是一个and（连乘）的形式，由此取条件期望为风险函数：

　　

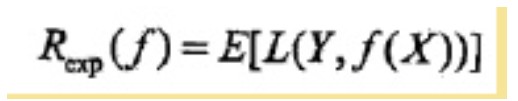
　　所谓条件期望，就是指X=x时，Y的期望。上式其实可以这么推回去：Ex∑［L（）］P（ck|X）=∑P（X）∑［L（）］P（X，ck）/P（X）=∑［L（）］P（X，ck）=E［L（）］，格式比较乱，但愿意思到了。为了最小化上式，只需对每个X=x执行最小化，那么加起来肯定是极小化的，由此有：

　　

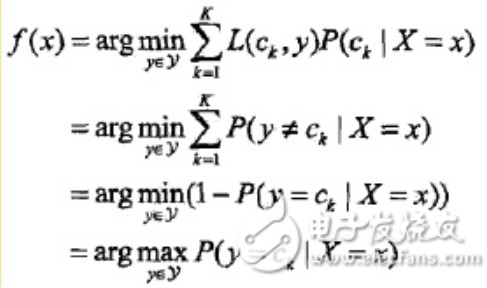
　　参数估计

　　极大似然估计：

　　前面说过，朴素贝叶斯法要学习的东西就是P（Y=ck）和P（X=x|Y=ck），这两个概率的估计用极大似然估计法（简单讲，就是用样本猜测模型参数，或者说使得似然函数最大的参数）进行：

　　

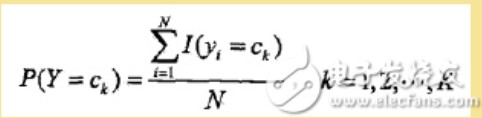
　　也就是用样本中ck的出现次数除以样本容量：

　　

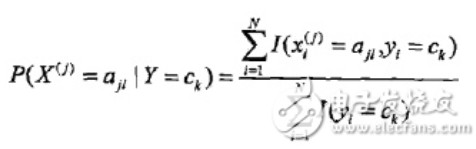
　　分子是样本中变量组合的出现次数，分母是上面说过的样本中ck的出现次数。

　　贝叶斯估计：

　　最大似然估计有个隐患，假设训练数据中没有出现某种参数和类别的组合怎么办？此时估计的概率值为0，但是这不代表真实数据中就没有这样的组合。解决办法是采用贝叶斯估计，以下显示的是先验概率的贝叶斯估计和条件概率的贝叶斯估计：

　　

　　分子和分母分别比最大似然估计多了一点东西，其意义是在随机变量每个取值的频数上加一个常量，当此常量取0时，就是最大似然估计，当此常量取1时，称为拉普拉斯平滑，常用来解决零概率的问题。

　　算法流程

　　总结如下算法流程：