

基于Gabor小波与RBF神经网络的人脸识别新方法
触控感测
描述
Gabor小波与人类视觉系统中简单细胞的视觉刺激响应非常相似。它在提取目标的局部空间和频率域信息方面具有良好的特性。虽然Gabor小波本身并不能构成正交基,但在特定参数下可构成紧框架。Gabor小波对于图像的边缘敏感,能够提供良好的方向选择和尺度选择特性,而且对于光照变化不敏感,能够提供对光照变化良好的适应性。上述特点使Gabor小波被广泛应用于视觉信息理解。二维Gabor小波变换是在时频域进行信号分析处理的重要工具,其变换系数有着良好的视觉特性和生物学背景,因此被广泛应用于图像处理、模式识别等领域。与传统的傅立叶变换相比,Gabor小波变换具有良好的时频局部化特性。即非常容易地调整Gabor滤波器的方向、基频带宽及中心频率从而能够最好的兼顾信号在时空域和频域中的分辨能力
rbf神经网络即径向基函数神经网络(Radical Basis Function)。径向基函数神经网络是一种高效的前馈式神经网络,它具有其他前向网络所不具有的最佳逼近性能和全局最优特性,并且结构简单,训练速度快。同时,它也是一种可以广泛应用于模式识别、非线性函数逼近等领域的神经网络模型。
人脸识别是人类最杰出的认知能力之一,让汁算机具有人的智能,使它可以象人类一样辨认人,一直是众多计算机科学工作者追求的目标。人脸识别作为一种应用前景十分广泛的身份鉴别方法,是模式识别领域极富挑战性的一个热点研究问题。
人脸图像由于受光照、表情以及姿态等因素的影响,同一个人的脸像矩阵差异也比较大,人脸识别所选取的特征必须对上述因素具备一定的稳定性和不变性。Gabor小波是Gabor变换与小波理论相结合的产物,它继承了小波变换的多分辨率特性,同时具有GaborN数本身所具有的局域性和方向性。VD Malsburg小组最先将Gabor小波引入人脸识别领域,应用Gabor小波与弹性图匹配技术相结合取得了良好的识别效果。Gabor小波核函数具有与哺育动物大脑皮层简单细胞的二维反射区相同的特性,即具有较强的空间位置和方向选择性,并且能够捕捉对应于空间和频率的局部结构信息;Gabor滤波器对于图像的亮度和对比度变化以及人脸姿态变化具有较强的健壮性,并且它表达的是对人脸识别最为有用的局部特征。
提高神经网络的泛化能力问题是RBF网络的一个重要研究方向。目前,提高网络泛化能力的研究主要集中在如何选取恰当的网络规模,即网络结构设计问题上。关于RBFN络结构设计,一个公认的指导原则是Moody准则,即:在没有其它先验知识的情况下,与给定样本一致的规模最小的网络就是最好的选择。
本文充分利用人脸特征矢量的相对分布信息,提出了一种新的聚类初始化方法,能使RBFN络逼近于Moody准则下的最优结构,从而保证该网络具有较好的泛化能力。由于在隐层参数固定的条件下,线性方程组的最小二乘解就是全局最优解,所以本文采用混合学习算法:由线性最小二乘法计算隐层和输出层之间的连接权值,由梯度下降法调整隐层神经元的中心和宽度。这种方法与单纯采用梯度下降法相比,学习速度更快,而且可以避免局部极小值问题。同时提出了一种有效的学习速率估算方法,使得RBF网络的整个学习过程具备自适应能力。
基于Gabor小波的人脸特征提取
构造Gabor小波
Gabor小波核函数定义如下:本文引用地址:
http://www.eepw.com.cn/article/157900.htm
上式表示一个经过高斯包络调制过的正弦波,其中

控制高斯窗口的宽度以及正弦波的波长,φ控制整个滤波器的方向,改变φ可以对滤波器进行旋转,σ为高斯窗的宽度与正弦波的波长之比。ψk经过平移、旋转和尺度变化形成一个自相似的函数族,即Gabor滤波器组。
对于数字图像,需要把参数k的模||k||和方向参数φ进行离散化,通常在5个对数空间频率v∈{0…,4}8个方向μ∈{0,…,7}上采样。针对人脸图像本文通过实验确定在2个空问频率v∈{1,2}和8个方向μ∈{0,…,7}上进行采样,形成16个Gabor滤波器。
人脸图像Gabor滤波
将人脸灰度图像插值为128×128(记为I),再分别与各个Gabor滤波器进行卷积,得到人脸图像的Gabor小波表示:

称Oμ,v(z)为Gabor人脸,其中z=(x,y)为相对于频谱中心的相对坐标值。通过二维快速傅立叶变换,将时域卷积变换为频域乘积运算以提高计算速度。
小波分解降维
每幅Gabor人脸图像Oμ,v(z)都是与I(z)同样大小的复数矩阵,取其幅值系数作为特征。通过参数μ,v的变化,Oμ,v(z)表达不同频率和方向的人脸特征信息,将一幅人脸的全部Gabor特征组成矢量,则人脸的原始特征数据高达262144维,后续处理非常困难。ChenKiun Liu分别取采样因子ρ=4,16,64进行下采样处理,所得识别结果相差很小,所以采样法最低可以得到4096维。而小波变换是一种常用的图像压缩方法,与采样法相比具有能量和信息损失小的优点。Harmon指出16×16的图像对于人脸识别是最基本的。因而,本文对Gabor人脸进行3次小波分解,将其低频近似图按行连接起来组成列矢量,并将全部列矢量依次连接起来,即为一幅人脸的低维Gabor特征列矢量。
主分量分析
设n为训练样本数目,Xi表示第i幅人脸图像的L维Gabor特征列矢量,则训练样本集的总体散布矩阵表示为:

式中
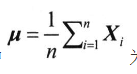
为样本均值。由于St为实对称矩阵(L×L),可将St化成对角形
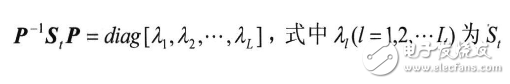
的特征值,P为正交变换矩阵,且特征值均非负值,令λ1≥λ2≥…λL≥0,λl对应的正交归一化特征向量为ul,则u1,u2,…,uL可以构成RL空间的一组标准正交基,在该正交特征空间中,人脸样本Xi可以表示为:

选用前r(rL)个较大特征值对应的特征向量作为正交基底(主分量),将Xi向该正交空间的子空间投影则有:
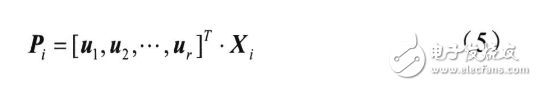
得到Pi=xi(1),xi(2),…,xi(r)为一组坐标系数,代表了Xi在新特征子空间中的位置,可将r维投影系数Pi作为人脸特征矢量输入分类器进行识别。
基于RBF神经网络的分类器设计
RBF神经网络的结构如图1所示,它是一种三层前向网络,其中r、u和s分别为输入层、隐层和输出层的节点数。
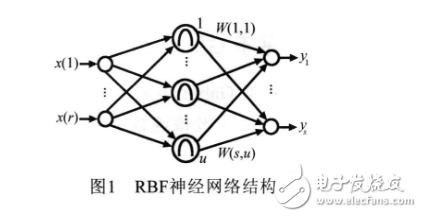
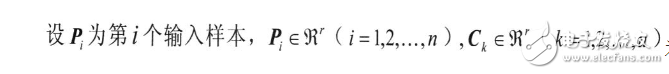
为隐层第k个神经元的中心,则隐层节点k的输出为:
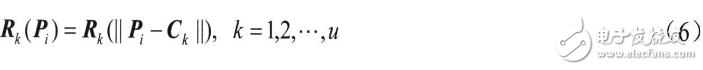
式中||・||表示欧氏范数。当RBF选用高斯核函数时,其输出为:
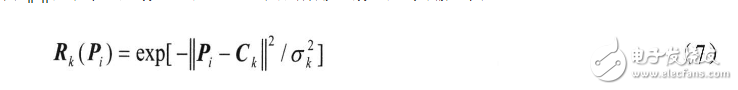
式中σk为隐层第k个神经元的宽度。输出层第j个节点的输出值yj为:

式中W(j,k)为隐层节点k到第j个输出节点的连接权值。
RBF网络初始化
RBF神经网络可看作是从特征子空间到类的映射,因此输入层的节点数与输入特征矢量的维数r相等,输出层的节点数就是待分类样本的类别数。隐层节点的选取是一个开放的问题,在理想情况下,隐层节点数取得最小值为样本类别数。每个人最多对应2~3个隐层节点,隐层聚类的初始化过程如下:
1)先假设每人收敛于一个聚类中心,将隐层节点数初始化为输出层节点数。
2)隐层第k个神经元的中心Ck为k类特征矢量的均值。
3)计算k类各个样本到中心Ck的距离,以最远点Pk(f)到中心的距离作为σk的初值。
4)计算各个聚类中心j到聚类中心k的距离:
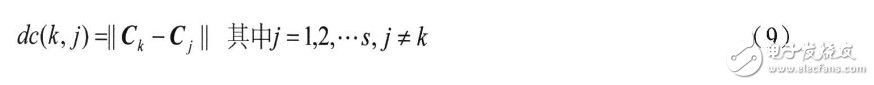
其中,最小距离为:
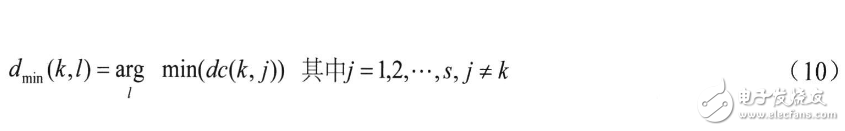
根据dmin(k,l)与dk,dl的关系,可将k类分为如下几种情况:
a)若dk+dl≤dmin(k,l),则k类与其它类没有重叠,如图2(a)所示;
b)若dk+dl》dmin(k,l),则k类与其它类相交。进一步分为两种情况:
i)dk一dldmin(k,l),如图2(b)所示;
ii)dk一dl≥dmin(k,l),如图2(c)所示,表示k类包含其它类,可能导致RBF神经网络分类错误。
5)对每类样本,依次按照以下两个规则进行判别并细分:
i)包含规则:若dk+dl》dmin(k,l)且dk一dl≥dmin(k,l),则k类包含其它类,必须将k类细分为两个聚类;
ii)正确归类规则:若k类包含其它类样本的个数大于1,必须将k类细分为两个聚类。
-
如何设计人脸识别的神经网络2024-07-04 1484
-
Matlab RBF神经网络及其实例2023-07-19 2310
-
神经网络及BP与RBF的比较2021-06-18 989
-
基于FPGA的RBF神经网络硬件实现2021-04-28 1069
-
基于RBF神经网络的辨识2017-12-06 1260
-
基于BP神经网络的人脸识别方法2017-12-01 2759
-
基于RBF神经网络的通信用户规模预测模型2017-11-22 1220
-
基于BP神经网络和局部与整体奇异值分解的人脸识别2017-07-29 1234
-
一种卷积神经网络和极限学习机相结合的人脸识别方法_余丹2017-01-08 1210
-
基于GA优化T_S模糊神经网络的小电流接地故障选线新方法_王磊2016-12-31 762
-
基于Gabor小波的人脸表情特征提取研究2012-02-29 1064
-
基于贝叶斯分类器和径向基函数(RBF)网络融合的人脸识别方法的设计方案2009-10-23 5289
-
基于RBF神经网络的软仪表的开发2009-08-14 564
全部0条评论

快来发表一下你的评论吧 !

