MLE极大似然估计和EM最大期望算法

　　机器学习十大算法之一：EM算法。能评得上十大之一，让人听起来觉得挺NB的。什么是NB啊，我们一般说某个人很NB，是因为他能解决一些别人解决不了的问题。神为什么是神，因为神能做很多人做不了的事。那么EM算法能解决什么问题呢？或者说EM算法是因为什么而来到这个世界上，还吸引了那么多世人的目光。

　　我希望自己能通俗地把它理解或者说明白，但是，EM这个问题感觉真的不太好用通俗的语言去说明白，因为它很简单，又很复杂。简单在于它的思想，简单在于其仅包含了两个步骤就能完成强大的功能，复杂在于它的数学推理涉及到比较繁杂的概率公式等。如果只讲简单的，就丢失了EM算法的精髓，如果只讲数学推理，又过于枯燥和生涩，但另一方面，想把两者结合起来也不是件容易的事。所以，我也没法期待我能把它讲得怎样。希望各位不吝指导。

　　EM算法 ：

　　相信大家对似然函数已经手到擒来了。那么我们就来看看高深的。

　　一个概率模型有时候既含有观察变量，有含有隐变量。如果只有观察变量那么我们可以用最大似然法（或者贝叶斯）估计未知参数，但是如果还含有隐变量就不能如此简单解决了。这时候就需要EM算法。

　　大家可能对这种问题不是很明白，也不太明白隐变量是什么意思。我举个例子（引用统计学习方法的例子）：

　　有3枚硬币分别记为A，B，C，并且出现正面概率分别为p ，q ，k.规则如下：先抛硬币A，如果为正面就选择B，否则选择C，然后再将选择的硬币（B或者C抛），然后观测结果。正面为1 反面为0.独立重复实验10次结果如下：1，1，1，0，0，0，1，1，1，0。我们并不知道抛A硬币时为正面还是方面，只知道最后的结果，问如何估计p，q，k的值？

　　如果我们知道抛的是哪个硬币就可以使用最大似然估计来估计这些参数，但是我们不知道。因为有p的原因，所以无法估计，这个p就是隐变量

　　log（Θ）=Σlogp（x;Θ）=Σlogp（x，p;Θ），Θ就是要求的q，k 待定参数，x为观测数据，因为这个p导致我们无法求解MaxΣlogp（x;Θ）。

　　还比如说调查 男生 女生身高的问题。身高肯定是服从高斯分布。以往我们可以通过对男生抽样进而求出高斯分布的参数，女生也是，但是如果我们只能知道某个人的高度，却不能知道他是男生或者女生（隐含变量），这时候就无法使用似然函数估计了。这个时候就可以使用EM方法。

　　分为E和M两步：

　　E步：

　　首先通过随机赋值一个我们要求的参数，然后求出另外一个隐含参数的后验概率。这是期望计算过程，我们首先通过随便赋予模型参数的初始值p，q，k，求出各个数据到模型的结果。

　　M步

　　用求出来的隐含参数的后验概率进行对传统的似然函数估计，对要求参数进行修正。迭代直到前后两次要求的参数一样为止

　　其实可以这么简单理解：就是在无监督聚类的时候，我们不知道模型的参数（比如为高斯分布），这时候我们就随便赋值给模型的待定参数（u和ó）。然后我们就可以计算出各个数据分别属于那一类。然后我们用这些分类好的数据重新估计u和ó。

　　EM算法推导

　　假设我们有一个样本集{x（1），…，x（m）}，包含m个独立的样本。但每个样本i对应的类别z（i）是未知的（相当于聚类），也即隐含变量。故我们需要估计概率模型p（x，z）的参数θ，但是由于里面包含隐含变量z，所以很难用最大似然求解，但如果z知道了，那我们就很容易求解了。

　　对于参数估计，我们本质上还是想获得一个使似然函数最大化的那个参数θ，现在与最大似然不同的只是似然函数式中多了一个未知的变量z，见下式（1）。也就是说我们的目标是找到适合的θ和z让L（θ）最大。那我们也许会想，你就是多了一个未知的变量而已啊，我也可以分别对未知的θ和z分别求偏导，再令其等于0，求解出来不也一样吗？

　　

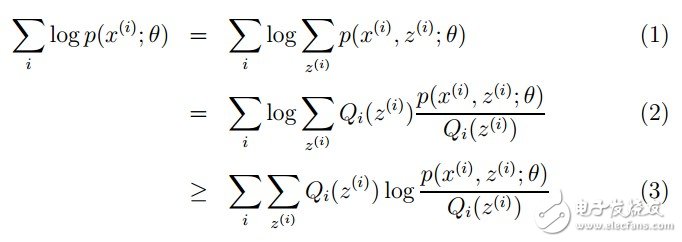
　　本质上我们是需要最大化（1）式（对（1）式，我们回忆下联合概率密度下某个变量的边缘概率密度函数的求解，注意这里z也是随机变量。对每一个样本i的所有可能类别z求等式右边的联合概率密度函数和，也就得到等式左边为随机变量x的边缘概率密度），也就是似然函数，但是可以看到里面有“和的对数”，求导后形式会非常复杂（自己可以想象下log（f1（x）+ f2（x）+ f3（x）+…）复合函数的求导），所以很难求解得到未知参数z和θ。那OK，我们可否对（1）式做一些改变呢？我们看（2）式，（2）式只是分子分母同乘以一个相等的函数，还是有“和的对数”啊，还是求解不了，那为什么要这么做呢？咱们先不管，看（3）式，发现（3）式变成了“对数的和”，那这样求导就容易了。我们注意点，还发现等号变成了不等号，为什么能这么变呢？这就是Jensen不等式的大显神威的地方。

　　Jensen不等式：

　　设f是定义域为实数的函数，如果对于所有的实数x。如果对于所有的实数x，f（x）的二次导数大于等于0，那么f是凸函数。当x是向量时，如果其hessian矩阵H是半正定的，那么f是凸函数。如果只大于0，不等于0，那么称f是严格凸函数。

　　Jensen不等式表述如下：

　　如果f是凸函数，X是随机变量，那么：E［f（X）］》=f（E［X］）

　　特别地，如果f是严格凸函数，当且仅当X是常量时，上式取等号。

　　如果用图表示会很清晰：

　　

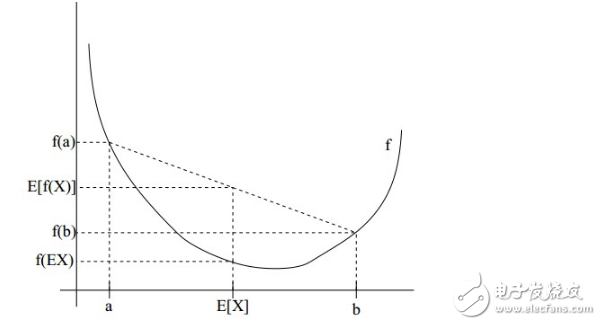
　　图中，实线f是凸函数，X是随机变量，有0.5的概率是a，有0.5的概率是b。（就像掷硬币一样）。X的期望值就是a和b的中值了，图中可以看到E［f（X）］》=f（E［X］）成立。

　　当f是（严格）凹函数当且仅当-f是（严格）凸函数。

　　Jensen不等式应用于凹函数时，不等号方向反向。

　　回到公式（2），因为f（x）=log x为凹函数（其二次导数为-1/x2《0）。

　　（2）式中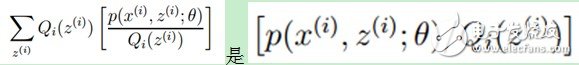的期望，（考虑到E（X）=∑x*p（x），f（X）是X的函数，则E（f（X））=∑f（x）*p（x）），又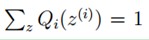，所以就可以得到公式（3）的不等式了（若不明白，请拿起笔，呵呵）：

　　

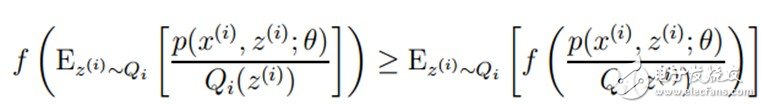
　　OK，到这里，现在式（3）就容易地求导了，但是式（2）和式（3）是不等号啊，式（2）的最大值不是式（3）的最大值啊，而我们想得到式（2）的最大值，那怎么办呢？

　　现在我们就需要一点想象力了，上面的式（2）和式（3）不等式可以写成：似然函数L（θ）》=J（z，Q），那么我们可以通过不断的最大化这个下界J，来使得L（θ）不断提高，最终达到它的最大值。

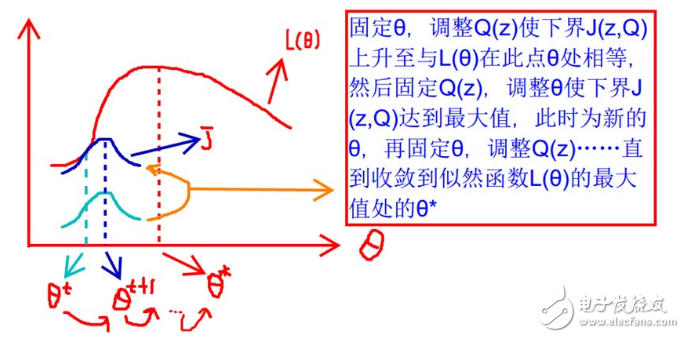
　　见上图，我们固定θ，调整Q（z）使下界J（z，Q）上升至与L（θ）在此点θ处相等（绿色曲线到蓝色曲线），然后固定Q（z），调整θ使下界J（z，Q）达到最大值（θt到θt+1），然后再固定θ，调整Q（z）……直到收敛到似然函数L（θ）的最大值处的θ*。这里有两个问题：什么时候下界J（z，Q）与L（θ）在此点θ处相等？为什么一定会收敛？

　　首先第一个问题，在Jensen不等式中说到，当自变量X是常数的时候，等式成立。而在这里，即：

　　

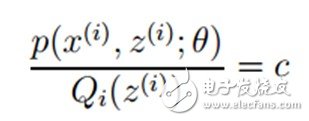
　　再推导下，由于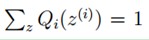（因为Q是随机变量z（i）的概率密度函数），则可以得到：分子的和等于c（分子分母都对所有z（i）求和：多个等式分子分母相加不变，这个认为每个样例的两个概率比值都是c），则：

　　

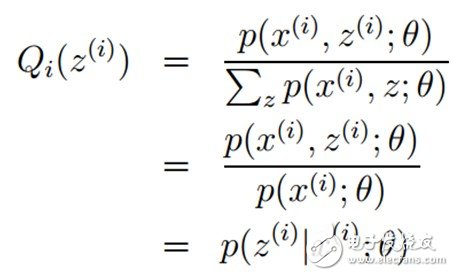
　　至此，我们推出了在固定参数θ后，使下界拉升的Q（z）的计算公式就是后验概率，解决了Q（z）如何选择的问题。这一步就是E步，建立L（θ）的下界。接下来的M步，就是在给定Q（z）后，调整θ，去极大化L（θ）的下界J（在固定Q（z）后，下界还可以调整的更大）。

　　举个例子：

　　假设我们有一个袋子，里面装着白球和黑球，但是我们不知道他们分别有多少个，这时候需要我们估计每次取出一个球是白球的概率是多少？如何估计呢？ 可以通过连续有放回的从袋子里面取一百次，看看是白球还是黑球。假设取100次里面 白球占70次，黑球30次。设抽取是白球的概率为P。 那么一百次抽取的总概率为 p（x;p）

　　p（x;p）=p（x1，x2.。。。。。.x100;θ）=p（x1;θ）*p（x2;θ）。。。。。。。.p（x100;θ）

　　=p70*（1-p）30

　　那么这时候我们希望可以使这个概率最大。

　　求导：logp（x;p）=logp70*（1-p）30 另导数为0则可以求出p=0.7（同理可以用到连续变量里面，这时候就是概率密度函数的乘积so easy）

　　是不是很简单，对！就是这么简单！其实最大似然估计就是在给定一组数据和一个待定参数模型，如何确定这个模型未知参数，使得这个确定后的参数模型产生的已知数据概率最大。当然这里我只是举了一个只有一个未知参数的估计方法，多个未知参数的做法是一样的，就是求似然函数求导取最大值。其实并不是所有似然函数都可以求导的，当似然函数无法求导时就需要根据定义求使得L（θ）最大的θ。

　　举个例子，以抛筛子为例：

　　

　　.最大后验估计 （MAP）：

　　最大后验估计就是在原来的MLE的基础上加上了先验知识：

　

　　EM算法另一种理解

　　坐标上升法（Coordinate ascent）：

　　

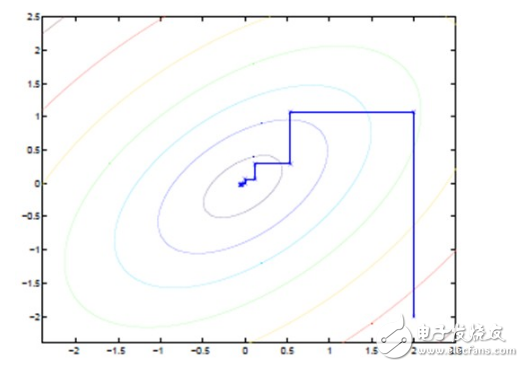
　　图中的直线式迭代优化的路径，可以看到每一步都会向最优值前进一步，而且前进路线是平行于坐标轴的，因为每一步只优化一个变量。

　　这犹如在x-y坐标系中找一个曲线的极值，然而曲线函数不能直接求导，因此什么梯度下降方法就不适用了。但固定一个变量后，另外一个可以通过求导得到，因此可以使用坐标上升法，一次固定一个变量，对另外的求极值，最后逐步逼近极值。对应到EM上，E步：固定θ，优化Q；M步：固定Q，优化θ；交替将极值推向最大。