

K均值聚类算法的MATLAB实现
电子常识
描述
K-means算法是最简单的一种聚类算法。算法的目的是使各个样本与所在类均值的误差平方和达到最小(这也是评价K-means算法最后聚类效果的评价标准)
K-means聚类算法的一般步骤:
初始化。输入基因表达矩阵作为对象集X,输入指定聚类类数N,并在X中随机选取N个对象作为初始聚类中心。设定迭代中止条件,比如最大循环次数或者聚类中心收敛误差容限。
进行迭代。根据相似度准则将数据对象分配到最接近的聚类中心,从而形成一类。初始化隶属度矩阵。
更新聚类中心。然后以每一类的平均向量作为新的聚类中心,重新分配数据对象。
反复执行第二步和第三步直至满足中止条件。
K-均值聚类法的概述
之前在参加数学建模的过程中用到过这种聚类方法,但是当时只是简单知道了在matlab中如何调用工具箱进行聚类,并不是特别清楚它的原理。最近因为在学模式识别,又重新接触了这种聚类算法,所以便仔细地研究了一下它的原理。弄懂了之后就自己手工用matlab编程实现了,最后的结果还不错,嘿嘿~~~
简单来说,K-均值聚类就是在给定了一组样本(x1, x2, 。。.xn) (xi, i = 1, 2, 。。。 n均是向量) 之后,假设要将其聚为 m(《n) 类,可以按照如下的步骤实现:
Step 1: 从 (x1, x2, 。。.xn) 中随机选择 m 个向量(y1,y2,。。.ym) 作为初始的聚类中心(可以随意指定,不在n个向量中选择也可以);
Step 2: 计算 (x1, x2, 。。.xn) 到这 m 个聚类中心的距离(严格来说为 2阶范数);
Step 3: 对于每一个 xi(i = 1,2,。。.n)比较其到 (y1,y2,。。.ym) 距离,找出其中的最小值,若到 yj 的距离最小,则将 xi 归为第j类;
Step 4: m 类分好之后, 计算每一类的均值向量作为每一类新的聚类中心;
Step 5: 比较新的聚类中心与老的聚类中心之间的距离,若大于设定的阈值,则跳到 Step2; 否则输出分类结果和聚类中心,算法结束。
单介绍下kmeans算法流程:
假设要把样本集分为c个类别,算法描述如下:
(1)适当选择c个类的初始中心;
(2)在第k次迭代中,对任意一个样本,求其到c各中心的距离,将该样本归到距离最短的中心所在的类;
(3)利用均值等方法更新该类的中心值;
(4)对于所有的c个聚类中心,如果利用(2)(3)的迭代法更新后,值保持不变,则迭代结束,否则继续迭代。
该算法的最大优势在于简洁和快速。算法的关键在于初始中心的选择和距离公式。
matlab实现:
function [ class count]=k_means(data,k);
%clear
%load testdata.mat
%k=2;
sum=size(data,1);
for i=1:k
centroid(i,:)=data(floor(sum/k)*(i-1)+1,:);
end
tic
ck=0;
while 1
temp=zeros(1,2);;
count=zeros(1,k);
ck=ck+1
for i=1:sum
for j=1:k
dist(j)=norm(data(i,:)-centroid(j,:));
end
[a min_dist]=min(dist);
count(min_dist)=count(min_dist)+1;
class(min_dist,count(min_dist))=i;
end
%重新计算类中心
for i=1:k
for j=1:count(i)
temp=temp+data(class(i,j),:);
end
temp_centroid(i,:)=temp/(count(i));
temp(1,:)=0;
% temp_centroid(i,:)=re_calculate(class(i,:),count(i),tdata);
end
%计算新的类中心和原类中心距离centr_dist;
for i=1:k
centr_dist(i)=norm(temp_centroid(i,:)-centroid(i,:));
end
if max(centr_dist)《=0
break;
else
for i=1:k
centroid(i,:)=temp_centroid(i,:);
%重新进行前俩不
end
end
end
toc
数据点是鼠标插进去的,通过界面可以很清晰的看到分类过程,功能截图如下:
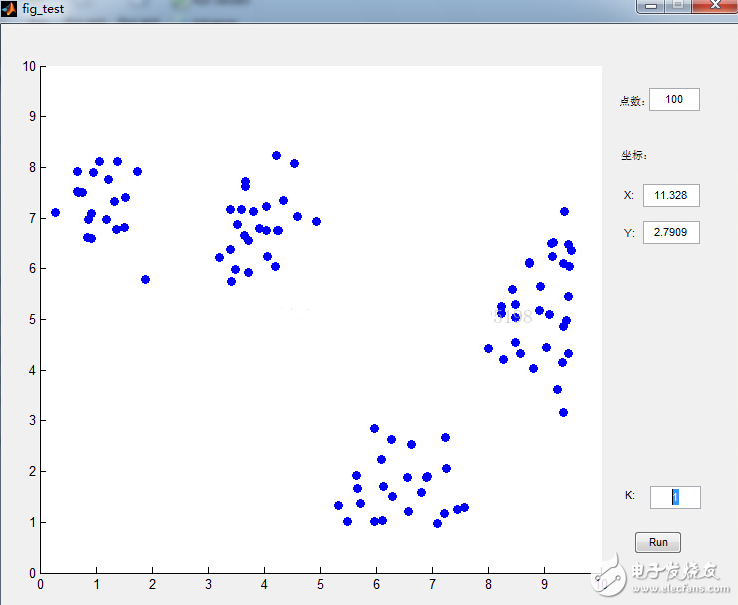
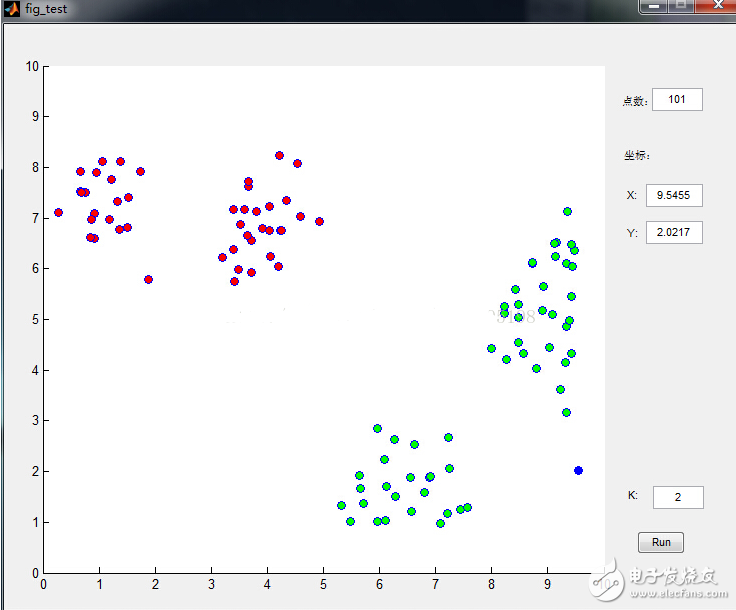
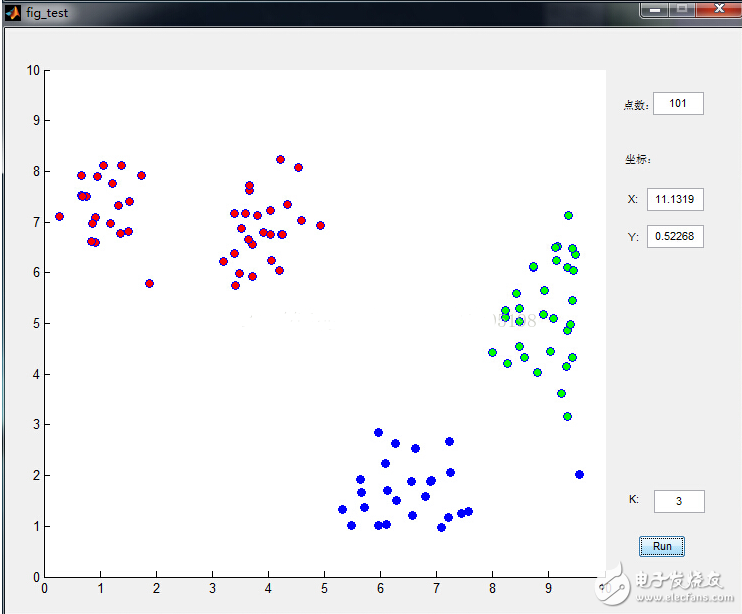
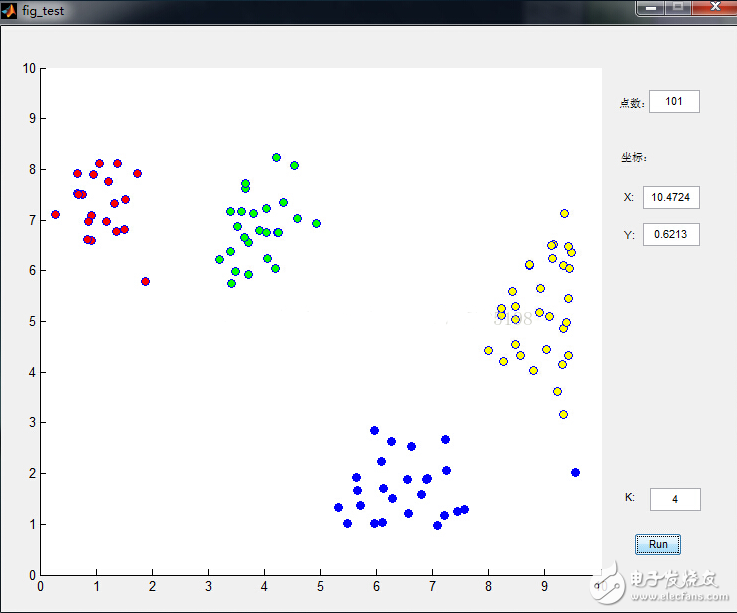
下面来看看K-means是如何工作的:
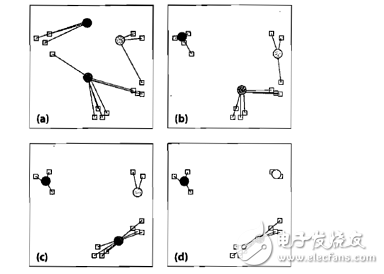
图中圆形为聚类中心,方块为待聚类数据,步骤如下:
(a)选取聚类中心,可以任意选取,也可以通过直方图进行选取。我们选择三个聚类中心,并将数据样本聚到离它最近的中心;
(b)数据中心移动到它所在类别的中心;
(c)数据点根据最邻近规则重新聚到聚类中心;
(d)再次更新聚类中心;不断重复上述过程直到评价标准不再变化
评价标准:
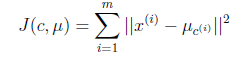
假设有M个数据源,C个聚类中心。µc为聚类中心。该公式的意思也就是将每个类中的数据与每个聚类中心做差的平方和,J最小,意味着分割的效果最好。
K-means面临的问题以及解决办法:
1.它不能保证找到定位聚类中心的最佳方案,但是它能保证能收敛到某个解决方案(不会无限迭代)。
解决方法:多运行几次K-means,每次初始聚类中心点不同,最后选择方差最小的结果。
2.它无法指出使用多少个类别。在同一个数据集中,例如上图例,选择不同初始类别数获得的最终结果是不同的。
解决方法:首先设类别数为1,然后逐步提高类别数,在每一个类别数都用上述方法,一般情况下,总方差会很快下降,直到到达一个拐点;这意味着再增加一个聚类中心不会显著减少方差,保存此时的聚类数。
MATLAB函数Kmeans
使用方法:
Idx=Kmeans(X,K)
[Idx,C]=Kmeans(X,K)
[Idx,C,sumD]=Kmeans(X,K)
[Idx,C,sumD,D]=Kmeans(X,K)
[…]=Kmeans(…,’Param1’,Val1,’Param2’,Val2,…)
各输入输出参数介绍:
X: N*P的数据矩阵,N为数据个数,P为单个数据维度
K: 表示将X划分为几类,为整数
Idx: N*1的向量,存储的是每个点的聚类标号
C: K*P的矩阵,存储的是K个聚类质心位置
sumD: 1*K的和向量,存储的是类间所有点与该类质心点距离之和
D: N*K的矩阵,存储的是每个点与所有质心的距离
[…]=Kmeans(…,‘Param1’,Val1,‘Param2’,Val2,…)
这其中的参数Param1、Param2等,主要可以设置为如下:
1. ‘Distance’(距离测度)
‘sqEuclidean’ 欧式距离(默认时,采用此距离方式)
‘cityblock’ 绝度误差和,又称:L1
‘cosine’ 针对向量
‘correlation’ 针对有时序关系的值
‘Hamming’ 只针对二进制数据
2. ‘Start’(初始质心位置选择方法)
‘sample’ 从X中随机选取K个质心点
‘uniform’ 根据X的分布范围均匀的随机生成K个质心
‘cluster’ 初始聚类阶段随机选择10%的X的子样本(此方法初始使用’sample’方法)
matrix 提供一K*P的矩阵,作为初始质心位置集合
3. ‘Replicates’(聚类重复次数) 整数
使用案例:
data=
5.0 3.5 1.3 0.3 -1
5.5 2.6 4.4 1.2 0
6.7 3.1 5.6 2.4 1
5.0 3.3 1.4 0.2 -1
5.9 3.0 5.1 1.8 1
5.8 2.6 4.0 1.2 0
[Idx,C,sumD,D]=Kmeans(data,3,‘dist’,‘sqEuclidean’,‘rep’,4)
运行结果:
Idx =
1
2
3
1
3
2
C =
5.0000 3.4000 1.3500 0.2500 -1.0000
5.6500 2.6000 4.2000 1.2000 0
6.3000 3.0500 5.3500 2.1000 1.0000
sumD =
0.0300
0.1250
0.6300
D =
0.0150 11.4525 25.5350
12.0950 0.0625 3.5550
29.6650 5.7525 0.3150
0.0150 10.7525 24.9650
21.4350 2.3925 0.3150
10.2050 0.0625 4.0850
-
FCM聚类算法以及改进模糊聚类算法用于医学图像分割的matlab源程序2018-05-11 3732
-
K均值聚类算法的MATLAB怎么实现?2021-06-10 1400
-
基于遗传算法的K均值聚类分析2009-04-13 490
-
模拟退火K均值聚类算法及其应用研究2009-09-15 642
-
优化初始值的K均值中文文本聚类2010-01-15 764
-
一种改进的粒子群和K均值混合聚类算法2010-02-09 827
-
K-means+聚类算法研究综述2012-05-07 739
-
特征加权和优化划分的模糊C均值聚类算法2017-01-07 964
-
基于改进K均值聚类的机械故障智能检测_费贤举2017-02-08 604
-
基于加速k均值的谱聚类图像分割算法改进_李昌兴2017-03-19 867
-
基于C均值聚类的定位算法2017-11-09 957
-
基于C均值聚类和图转导的半监督分类算法2017-11-28 697
-
基于混合蛙跳算法的K-mediods聚类算法2021-05-08 911
-
基于密度的改进K-均值聚类组合方法2021-05-31 823
全部0条评论

快来发表一下你的评论吧 !

