什么是基追踪算法?基于改进基追踪方法的信号去噪

　　什么是基追踪算法

　　基追踪（basis pursuit）算法是一种用来求解未知参量L1范数最小化的等式约束问题的算法。

　　基追踪是通常在信号处理中使用的一种对已知系数稀疏化的手段。将优化问题中的L0范数转化为L1范数的求解就是基追踪的基本思想。

　　比如我原先有一个优化问题：

　　min ||x||_0（就是L0范数的最小值）subject to y=Ax。

　　这个||x||_0，就是表示x中有多少个非零元素；那么我们要求min ||x||_0，就是想知道含有最多0元素的那个解x是什么。

　　但是呢，L0范数有非凸性，不怎么好求解，这时我们就转而求解L1范数的优化问题。

　　那么，基追踪算法就是转而求解

　　min||x||_1（就是L1范数的最小值）subject to||y-Ax||_2=0（2范数）

　　这个||x||_1，就是x的绝对值；那么我们要求min||x||_1，就是求绝对值最小的那个解x是什么。

　　更通俗一点来讲，比如我要求一个线性方程组

　　Ax=b

　　x就是我们要求的未知量。这个A矩阵不是个方阵，是个欠定矩阵，那么就导致这个线性方程组会有若干组解。那么我们到底要哪组解好呢？

　　如果在一般情况下，可以直接用最小二乘法来获得一组最小二乘解，就是x=（A‘A）^（-1）A’b。但是我们现在利用基追踪，就是想要来获得一组含0元素最多的解。

        提出了一种新的基追踪求解算法。依据信号特性自适应地选取字典；通过l1范数的近似表示，将有约束的极值问题转化为无约束问题，并利用一种新的迭代算法进行快速求解；几类典型信号实验结果验证了本方法具有良好的去噪效果。 关键词：基追踪 字典 去噪 基追踪方法是信号稀疏表示领域的一种新方法。它寻求从完备的（过完备）函数（基）集合中得到信号的最稀疏的表示，即用尽可能少的基精确地表示原信号，从而获得信号的内在本质特性。基追踪方法采用表示系统的范数作为信号稀疏性的度量，通过最小化l1范数将信号稀疏表示问题定义为一类有约束的极值问题，进而转化为线性规划问题进行求解。 目前，基追踪方法在一维信号处理领域有很好的应用。

　　以David L.Donoho为代表的斯需求量福大学统计系工作组利用基追踪方法在一维实信号去噪和超分辨方面取得取了很多很好的应用结果。尽管使用了一种新的线性规划算法——内点算法，基追踪方法由于要在所有的字典向量中极小化一个全局目标函数，其计算量仍然是很大的。正因为求解大尺度线性规划问题的困难，目前的基追踪方法局限于一维的信号去噪和超分辨处理。本文提出一种新的思路来求解上述有约束的极值问题。首先依据信号特性自适应地选取字典；通过l1范数的近似表示，将有约束的极值问题转化为无约束问题，并利用一种迭代算法进行快速求解；最后通过几类典型信号去噪实验来验证本方法的应用效果。实验结果表明，改进的基追踪方法能够快速稳定实现，。同时具有良好的去噪效果。

　　

　　1 字典的构造

       对于观测到的离散信号s∈H，H为Hilbert空间，给定H中的字典φ={φγ，γ∈Γ}，其中Γ为指标集，φγ为H中的基函数，也称为原子。基追踪方法将信号稀疏表示问题定义为以下有结束的极值问题，即

　　其中，αγ（γ∈Γ）为表示系数。如果将字典中的向量表示成矩阵φ的例，系数表示成一个列向量，则（1）式可表示成 min||α||1 subject to s=φα （2） 在含噪观测的情况下，考虑如下模型： y=s+σz 其中s为真实信号，y为观测信号，z为标准高斯白噪声，σ为噪声根方差。基追踪方法去噪归结为求解以下优化问题：

　

　　以上最优化问题致力于最小化信号重建误差，同时使得信号的表示最稀疏。正则化参数λ控制着允许误差与稀疏性之间的平衡。 由（3）式可见，基追踪方法去噪的核心问题涉及到原子的选取、字典的构造、求解算法设计等三个方面。其中，字典的构造是基追踪方法的重要环节。为了尽可能精确地表示信号，字典与信号应用是自适应的，或者说字节是从信号的学习中得到的。通常，基追踪方法所使用的字典有完备的、过完备的、欠完备的等。可以根据信号的先验信息及实际需要设计字典。一般设计的字典是完备或过完备的。对于简单信号去噪，一般只需要构造完备的字典。对于复合信号对噪问题，通常需要构造过完备的字典。对于完备字典，同样存在信号的稀疏表示问题，因为噪声总是处处奇异的。本文所采用的字典主要有： （1）Heaviside字典

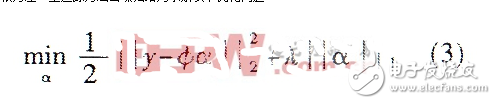
　　此字典中原子不是正交的，但是对于任意长度为n的一维离散信号s=（s1s2…sn）都有以下表示：

　　

　　Heaviside字典具有上三角形式，结构简单，善于捕捉分片常数信号中的突变特征。 （2）时间-尺度字典（小波字典） 以Haar小波字典为例： 你小波基：ψ=l［0，1］，母小波基：ψ=1［1/2，1］，1-1［0，1/2］ Haar小波字典中包含小波基的平移和伸缩变换以及小波基的平移变换。 设ψ=（a，b，v），其中α∈（0，∞）为尺度变量，b∈［0，n］表征位置，v∈{0，1}表征性别。Haar小波字典形式为：

　　

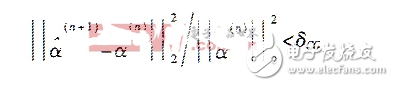
　　包含n个原子，构成一组正交基。当然还有其它类型的小波字典，尽管有些小波基没有类似Haar小波基这样明确的小波函数表达式，但它们的字典都有与Haar小波字典类似的离散结构。比较常用的主要用Daubechies、Coiflet、Symmlet等。小波字典应用于表示分片光滑信号。 （3）Heaviside字典+小波字典 对于比较复杂的复合信号，单一的字典下无法得到信号的最稀疏表示，此时可将几种字典合成，从而得到过完备的字典。例如Heaviside字典+小波字典。

     2 新的求解算法

     将（3）式等阶于如下二次规划问题：

　　

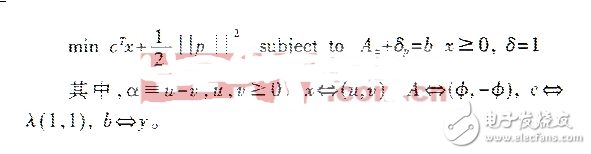
　　采用内点算法求解以上二次规划问题。这种算法收敛性能稳定，但由于它是一种大尺度的线性规划算法，复杂度高，所耗费的计算时间非常长，不便于实际应用，为此，针对（3）式，采用一种新的迭代算法来求解以上最优化问题。 首先，给出l1范数的平滑近似

　　

　　其中，N为向量z的长度，ε为非常小的常数（ε》0），本文取ε=10 -6）。

　　

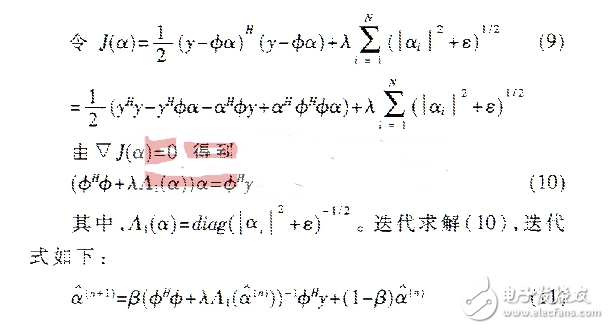
　　其中，β为迭代步长，0《β≤1，迭代初值可取α（0）=φHY。迭代的终止条件由

　　

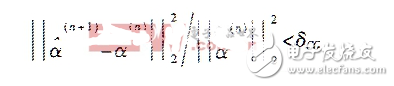
　　控制（本文取δcG=10 -3），这样即可得到优化问题的解α。在得到表示系数α的估计α后，可由s=φα得到的重构的信号。

     3 正则化参数λ的选取

      在所考虑的噪声为高斯白噪声以及对字典φ进行规范化（||φγ||2=1）的情况下，中λ的经验值取为

　　，

　　其中，P为字典φ的势。此经验值实际对应于正交基下小波小噪方法的中阈值。因此这种参数的选取方法依赖于对信号中的噪声方差的精确估计。而对噪声方差的精确估计通常是比较困难的。因此该经验值是一种次优值。可从另一个角度来考虑正则化参数的选取方法。容易证明，在对字典φ进行正交化后，目标函数具有单峰性质（目标函数为函数），因此可通过最小化目标函数，在迭代算法中用线性搜索的方法寻求最优。

　　4 实验结果

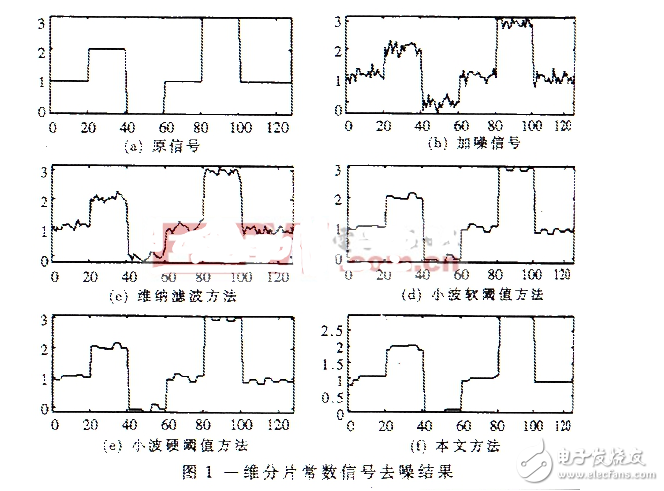
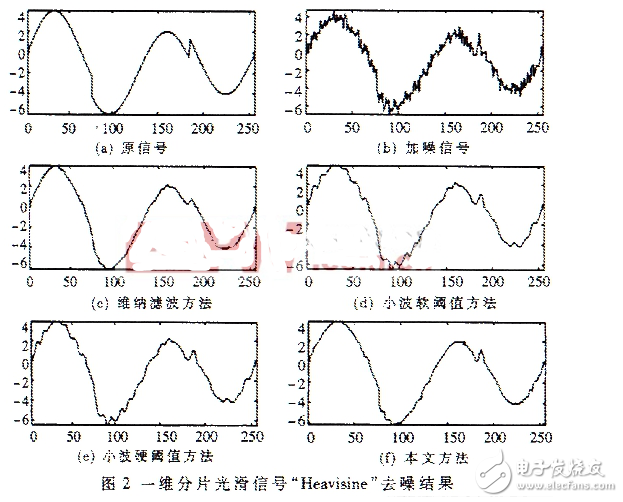
        为了验证本方法的去噪效果，将其应用于一维信号去噪实验，并与小波软、硬阈值去噪方法以及Wiener滤波方法进行了比较。 设计二组一维实信号，即分片常数信号和分片光滑信号。其中分片光滑信号“Heavisine”是由下式产生的一种信号：

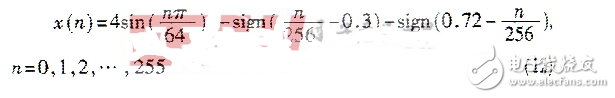
　　对二组信号附加高斯白噪声。其中第一组噪声根方差σ=0.2，第二组噪声根方差为σ=0.5。去噪结果如图1和图2所示。分片常数信号实验中的小波方法所采用的小波基为Haar小波基，分片光滑信号实验中的小波方法所采用的小波基为Sym8小波基。依据信号的特性，分片常数信号实验中基追踪方法采用Heaviside完备字典，分片光滑信号实验中基追踪方法采用Heaviside+Sym8小波字典合成的过完备字典。表1对各种方法的信噪比改善程度进行了比较。在配置为奔4 Celeron（1.8G）微机上运动未经优化的Matlab程序，分片常数信号实验总过程耗时约9s，分片光滑信号实验总过程耗时约80s。表1 信噪比的比较结果 SNR含噪信号Wiener波波小波软阈值方法小波硬阈值方法本文方法分片常数信号18.33dB22.02dB24.91dB24.03dB25.99dB分片光滑信号16.13dB22.41dB21.78dB21.75dB24.69dB理论分析和实验结果表明，该方法能够快速稳定实现，同时具有良好的去噪效果。与传统去噪方法相比，基追踪方法对于信噪比的改进程程度更高，同时它能有效地保持信号中的重要特征。