图像的分形维数研究与分析

　　分形维数简介

　　分形维数被誉为大自然的几何学的分形（Fractal）理论，是现代数学的一个新分支，但其本质却是一种新的世界观和方法论。分维反映了复杂形体占有空间的有效性，它是复杂形体不规则性的量度。它与动力系统的混沌理论交叉结合，相辅相成。它承认世界的局部可能在一定条件下或过程中，在某一方面（形态，结构，信息，功能，时间，能量等）表现出与整体的相似性，它承认空间维数的变化既可以是离散的也可以是连续的，进而拓展了视野。

　　分形维数原理

　　fractal dimension主要描述分形最主要的参量，简称分维。通常欧几里德几何中，直线或曲线是1维的，平面或球面是2维的，具有长、宽、高的形体是 3 维的；然而对于分形如海岸线、科赫曲线、谢尔宾斯基海绵等的复杂性无法用维数等于 1、2、3 这样的数值来描述。科赫曲线第一次变换将1英尺的每边换成3个各长4英寸的线段，总长度变为 3×4×4/3=16 英寸；每一次变换使总长度变为乘以4/3，如此无限延续下去，曲线本身将是无限长的。这是一条连续的回线，永远不会自我相交，回线所围的面积是有限的，它小于一个外接圆的面积。因此科赫曲线以它无限长度挤在有限的面积之内，确实是占有空间的 ，它比1维要多，但不及2维图形，也就是说它的维数在1和2之间，维数是分数。同样，谢尔宾斯基海绵内部全是大大小小的空洞，表面积是无限大，而占有的 3 维空间是有限的，其维数在2和3之间。

　　图像的分形维数研究与分析

　　1 分形基础

　　1. 1 分形理论

　　Mandelbrot 曾经为分形下过两个定义：（1） D（ A）》d（ A的集合 A，称为分形集，其中 ，D（ A）为集合A的 Hausdoff 维数（或分维数），d（ A）为其拓扑维数。一般说来 ，D（ A）不是整数，而是分数;（2）部分与整体以某种形式相似的形 ，称为分形。然而，经过理论和应用的检验，人们发现这两个定义很难包括分形如此丰富的内容。实际上，对于什么是分形，到目前为止还不能给出一个确切的定义，人们通常是列出分形的一系列特性来加以说明。 分形特性有：

　　（1）分形集具有精细的结构 ，即有任意小比例的细节 ;

　　（2）分形集是如此的不规则以至它的整体和局部都不能用传统的几何语言描述 ;

　　（3）分形集通常有某种自相似的性质 ，可能是近似的或是统计的 ;

　　（4）一般的 ，分形集的“分形维数”（以某种方式定义） 大于它的拓扑维数 ;

　　（5）在大多数令人感兴趣的情形下 ，分形集以非常简单的方法定义 ，可能由迭代产生。

　　1. 2 分形维数

　　在欧几里德空间 ，所有的物体的维数都是整数维的 ，而分形理论则把维数视为分数。 维数是分形几何理论中重要基本概念之一 ，目前已经有许多维数的定义 ，主要包括 Hausdorff 维数、计盒维数（Box2counting dimension） 、修正计盒维数、填充维数等。 在实际应用中 ，通常所说的分形维数都是指计盒维数 ，而在分形理论应用研究中提出的许多维数的概念都是计盒维数的变形。

　　2 分形维数在图像分析中的应用

　　分形理论在图像分析中的应用是基于以下两点为基础的 ：一是自然界中不同种类的形态物质一般具有不同的分维数 ;二是由 A. P. Pentland 的假设 ，自然界中的分形与图像的灰度表示之间存在着一定的对应关系

　　2. 1 分形维数在图像分类中的应用

　　李厚强等在对航空遥感图像进行分类时采用基于分形维数的方法计算纹理特征 ，以此来提取和分析遥感图像的结构特征 ，并与航空遥感图像的另一重要特征 ———光谱信息相结合 ，通过综合应用纹理信息和光谱信息实现对遥感图像的分析与识别。 尺度不变性是基于分形的纹理特征的一个重要特点 ，这非常适合遥感图像分类。 现有的基于分形模型的方法是以分形维数作为纹理特征 ，在计算分形维数时 ，该文章采用 N. Sarkar 和 B. B. Chaudhuri 提出的 DBC（Differential Box Counting） 方法。 其主要思想如下。

　　将 M ×M 大小的图像分割成 s ×s 的子块（ M/ 2 Ε s 》 1 ，s 为整数） ，令 r = s/ M 。 将图像想象成三维空间中的曲面 ， x ， y 表示平面位置 ， z 轴表示灰度值。 xy 平面被分割成许多s ×s的网格 ，在每个网格上 ，是一列 s ×s ×s的盒子。 设图像灰度在第（ i ， j）网格中的最小值和最大值分别落在第 k 和第 l 个盒子中 ，则 ：

　　nr （ i ， j） = l - k + 1 （4）

　　是覆盖第（ i ， j） 网格中的图像所需的盒子数 ，而覆盖整个图像所需的盒子数 N r 为

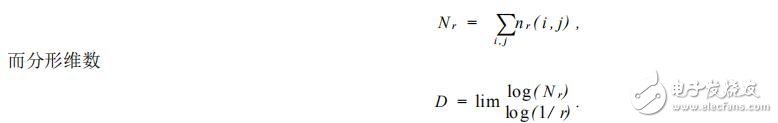
　　针对不同的 r，计算 N r ，应用最小二乘法 ，即可求得分形维数 D. 在实际应用中 ，仅以分形维数为特征 ，很难达到好的分类效果 ，于是 ，文章引入“空隙”特征的概念 ，并将高、低灰度图像变换作为纹理特征之一 ，结合图像的色度和饱和度 ，有效地避免了不同材料计算得出相同分形维数的情况 ，可以较为准确的对航空遥感图像进行分类。

　　基于分形维数的图像分类也可以应用于图像压缩的预处理 ，基于分形维数特征 ，将图像分为不同的区域 ，而这一分类 ，对图像进行进一步的压缩编码具有重要的指导意义。曹文伦等依据图像灰度变化的平缓或剧烈程度 ，将图像分为以下几类 ：纹理、纹理边缘、纹理边缘平滑、边缘平滑和平滑 ，并且分别计算以及确定了不同图像种类的分形维数区间。 按照此区间 ，可以对待测图像基于其分形维数进行分类。 利用分类结果 ，可以分析以及初步判断待测图像的空间不规则程度 ，对在进一步进行压缩编码具有指导意义。 如果一个物体的表面是分形的 ，则由它产生的图像灰度表面也具有分形的性质。 基于此 ，通过 Keller 的盒维数算法完成原图分形维数的提取。 其主要思想是：令离散灰度图像 F是一个在三维空间中的分形曲面 ，长、宽为 R; Nε（ F） 表示边长为ε×ε×ε的包含所要估计的图像区域 ，其分形维数 DB 将由（7） 式决定 ：

　　将 R ，ε带入（8） 式 ，即可求出灰度图像 F的盒维数 DB 。 分形维数可以很好的作为图像分析与分类的参数 ，该方法所使用的采用分形维数的图像分类与人凭借主观感受对图像进行的分类相吻合。

　　李杰等在对待压缩图像进行预处理时 ，把标准图像分为图像块 ，通过计算其分形维数 ，依据图像块内灰度及其变化情况 ，把图像块分为 3 类 ：均匀块、中值块和边缘块 ，不同种类的图像块反映了不同的纹理特征。 在对图像块分形维数特征的计算中 ，本文采用的是基于形态算子的毯子覆盖法计算图像块灰度图像的分形维数。 其主要思想是灰度图像想象成一个在三维空间中的分形曲面 ，所要估计的图像区域的分形维数 D 将由下面的公式确定

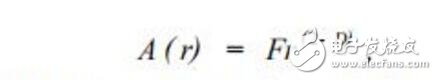
　　式中 A （ r） 为分形曲面的表面积 ， r为度量时所使用的面积元尺度 ， D为曲面的分形维数 ， F是一常数。 曲面的表面积求法如下 ：把三维空间中的所有距离曲面表面为 r的点 ，用厚度为2 r的毯子覆盖 ，曲面的表面积就是被覆盖的体积除以2 r，覆盖的毯子由曲面的上表面 ur 和下表面 br 来定义 ：设曲面上点（ i ， j） 的灰度值为 g（ i ， j） ，取 r = 1 ，2 ，3 ， …， ur ， br 的值为

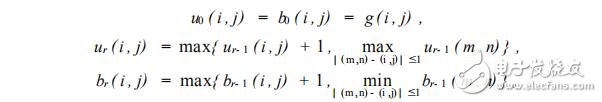
　　其中点（ m ， n） 是距离点（ i ， j） 不大于 1 的点 ，取于点（ i ， j） 的四邻域。 该毯子的体积为 ：

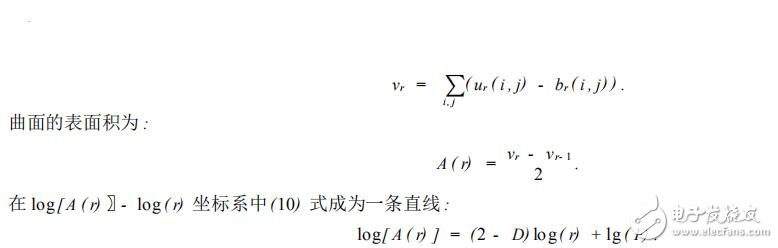
　　并在 log［ A （ r） ］2log （ r） 坐标系中做直线的最小二乘拟合 ，直线的斜率即为图像的分形维数 D.文中引入了α，β两个衍生参数作为分类辨别参数 ，以此来集中体现图像块的纹理特点。 将待测图像块的分形维数值与α，β相比较 ，并确定图像块的所属分类 ，依据分类 ，对不同的图像采用不同方式的压缩编码。 该方法基本正确的反映了图像中的纹理分布情况。 针对图像块的纹理分布情况 ，采用不同的压缩编码 ，可以得到较好的效果.

　　2. 2 分形维数在图像分割中的应用

　　薛笑荣等针对 SAR（合成孔径雷达） 图像包含相干斑噪声 ，导致传统方法不能很好对其分割的问题 ，考虑将 SAR 图像的特点和分形理论相结合 ，从而提出了一种新的 SAR 图像分割方法。 该方法首先对原始 SAR 图像每个像元为中心取两种不同窗口 ，计算在该两种窗口下基于区域自选的分形维数并求均值 ，将其作为分形纹理特征。 然后根据 SAR 图像噪声在小波域中的分布特点对 SAR 图像进行滤波 ，最后以 SAR 图像分形纹理特征和滤波后的灰度组成特征向量对 SAR 图像进行分割。 同样是针对严重的噪声干扰导致传统方法不能很好的完成图像分割的问题 ，彭复员等［11 ］提出通过图像分形维数和分形常数的特征来实现对激光水下图像纹理特征的分割。 该方法利用了毯子覆盖法 ，并在线性拟合计算分形维数（斜率） 的同时计算分形常数（截距） ，然后对这两个数据采用局部最佳阈值法 ，进行二维直方图阈值分割。

　　于向军等针对路面状况摄像检测过程中路面裂缝的图像分割问题 ，提出了利用分形理论进行图像分割的方法。 该方法根据路面裂缝图像的自相似性 ，通过对路面裂缝的分形特征进行聚类分析来识别图像的边缘。 首先计算图像的分形维数 D ，然后计算均值 mean 和方差σ。 通过以上计算可以得到一组分别表示裂缝图像的分形维数、图像的平均强度和图像灰度变化的剧烈程度的特征参数数据{ D ， mean σ， }。 最后采用 K2平均法通过分裂和合并的聚类过程实现将数据点集{ D ， mean σ， }作为聚类过程的原始数据通过判定得出聚类结果 ，这样每一小块就对应一个类别标号 ，将这些类别标号还原到它所对应的小子块上 ，即得分割结果图像。 该方法不仅可以提高图像分割的精度 ，而且显著的减少了图像处理的数据量和处理时间。 同样是针对分割路面裂缝的方法 ，王华等在差分计盒方法计算图像分形维数的基础上 ，提出一种差分计盒方法的改进算法 ，使用该方法计算路面图像的分形维数 ，所得的分形维数可以把简单的阈值应用到路面裂缝的分割。 该方法将差分计盒方法计算中盒子的长度改为 1/ 2n，首先取图像中固定大小的像素块 ，计算该像素块的分形维数 ，然后将像素块在图像上移动 ，计算像素块覆盖下的分形维数 ，接着画出分形维数的直方图。 因为小于维数 2 的图像块是在纹理的边沿上 ，所以 ，在分形维数等于 2 处 ，将直方图分开 ，则分形维数小于 2 的图像块就为裂缝的位置 ，从而实现了路面裂缝的图像分割。

　　针对遥感图像的特征提取与分割 ，郑桂香等利用双毯法［15 ］Double Blanket Method） 提取图像的分形特征并用于分割。首先 ，通过比较局部分形维数偏移全局分形维数的标准差确定适合该方法的最优滑动窗口。 其次 ，提取出多尺度的特征值并建立分形维数谱。 然后 ，分析图像中各区域的分维谱 ，选择适当尺度的分形特征 ，利用最大似然法对图像进行分割。 该方法可以显著的提高遥感图像的分割精度。 同样是针对遥感图像的分割问题 ，陈小梅等［16 ］针对遥感图像的分形特点 ，采用局部分形维数进行图像分割。 利用金字塔模型替代了局部分形计算中的窗口模板 ，从而对局部三角棱柱面法进行了改进 ，并设计了一种新的递归计算流程 ，有效的降低了内存存储量。 该方法提高了基于遥感图像纹理特征的图像分割方法的计算速度 ，同时保留了三角棱柱面法对于分形维数计算的准确性。 但是 ，如何解决分维计算中出现的“边缘效应”，自适应确定图像的自相似尺度范围以提高图像的分割精度 ，仍然有待进一步研究

　　2. 3 分形维数在图像边缘检测中的应用

　　张坤华等［17 ］通过分析 ，得出面积度量的分形参数系数 k ，并把它作为边缘检测分形特征。 使用地毯覆盖法计算分形维数 ，在估计出表面积 A （ε） 后计算 k. 该方法引入自适应阈值 T = a ·max k （ i ， j） 来完成边缘检测与提取。 黄寰等［18 ］在针对加性高斯白噪声的情况时 ，研究了 H 值小波变换计算方法。 而对分形参数的估计是首先滤波然后再差分 ，从而平滑和抑制噪声 ，实现了有噪图像的边缘检测。 罗强等［19 ］在进行边缘检测时 ，利用图像的子图分形结构差异和分形失真度的不同 ，采用自适应四叉树和邻近搜索相结合的方法 ，设定了分形编码阈值。 在搜索子块所对应的最佳匹配父块的过程中 ，把与父块的失真度大于阈值的子块划为边缘 ，通过零交叉和二值化来完成图像的边缘提取工作。

　　SAR 图像中包含大量的相干斑 ，且 SAR 图像内容复杂 ，特别是自然环境中随机变化的因素和复杂的纹理背景在很大程度上影响了边缘检测的准确性、适应性和实时性 ，这使得传统的边缘检测方法很难取得满意的效果。 针对以上问题 ，张红蕾等［20 ］使用多重分形维数描述图像的纹理。 首先计算原始 SAR 图像离散点数据的奇异性指数 ，然后对应每一点奇异性指数计算全局多重分形奇异谱 ，最后根据判决准则区分边缘和纹理从而实现 SAR 图像的边缘检测。 该方法能够检测到许多局部细节 ，同时又避免出现不重要的细节 ，突出了主要的边缘信息 ，很好的区分出 SAR 图像的纹理和边缘。 但是 ，如何同时使用几个测度来提高图像边缘的精度 ，还有待进一步研究。

　　3 结 论

　　自然物体和人工物体的图像在分形维数上存在着一定的差异 ，正是这个差异 ，使得分形理论和技术在图像分析中的应用成为可能。 盒维、差分盒维、毯子维等方法 ，是目前研究较为充分的方法 ，在很多领域都有着较为广泛的应用。 而结合小波、形态学、模式识别和神经网络以及多重分维计算等相关技术 ，是基于分形理论的图像分析方法的发展趋势 ，值得进一步关注和广泛深入研究。