对车用锂离子动力电池三种状态的SOC估算研究

锂电池已被广泛应用于工业、日常生活等领域，对电池荷电状态（SOC）的估算已成为电池管理的重要环节。但是，由于电池结构复杂，电池的荷电状态受放电电流、电池内部温度、自放电、老化等因素的影响，使得SOC的估算困难。目前SOC估算方法有：开路电压法、安时计量法、内阻法、神经网络和卡尔曼滤波法。国外V. Pop等人提出EMF-SOC模型［1-2］，即电池电动势与荷电状态的关系模型来估算SOC，相当于开路电压法，该方法用于电池静置足够长时间后进行估计，不能实时估计；也有人采用安时计量法或卡尔曼滤波法估计SOC，安时计量法由于电流波动较大或测量误差长时间积累导致估计不精确；卡尔曼滤波法则在建立准确实用的电池动态模型上存在很大困难，为此本文根据锂电池在应用中的实际情况，采用了一种新思路来估算SOC，即将电池的工作状况分为三种状态，对每种状态的SOC逐一进行估算，在估算过程中消除影响SOC的因素，且使三种状态下SOC的值互为前提，从而提高SOC的估算精度。

1、电池工作状态及SOC估计

电池状态根据实际情况可分为三种状态，这里将其定义为静止、恢复、充放电，它们的关系如图1。

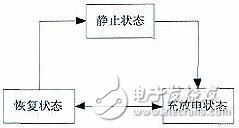
图1 电池工作状态图

1.1 静止状态

电池的静止状态是指电池工作停止后，完全恢复了的状态，从恢复状态转化而来，可直接转入充放电状态，此状态下SOC的计算量作为充放电状态下SOC估算的初始值。由于此状态下的特点是电流为零、无极化现象，其SOC值与开路电压有很好的对应关系，因此能用开路电压法直接估算电池的SOC值，电池的开路电压与SOC值的关系曲线如图2。

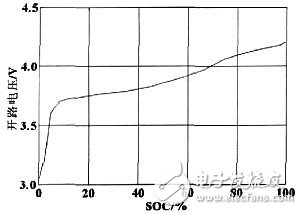
图2 电池的开路电压与SOC值的关系曲线

在静止状态下，电池容量主要受自放电现象的影响使得电池电量会随着时间的增加而减少，而用开路电压与SOC值的对应关系来估算SOC，本身就可以消除自放电引起的电量损失的影响，从而能使SOC值更加准确地反映电池的状态。

1.2 恢复状态

恢复状态是指电池从放电或充电状态转到静止状态的过渡阶段。一般这个阶段经历的时间为8h（此值为经验值），此状态下SOC的计算量作为充放电状态下SOC估算的初始值，这时的SOC估算主要考虑放电或充电结束后电池电量的改变量。从放电或充电状态进入恢复状态后电池电量会随时间增加而有所增加，其变化的原因是在放电或充电过程中电池内部产生极化现象，部分电量没有用于实际的充放电中而是慢慢累积起来，当电池停止工作后极化现象会慢慢消失，累积的电量也会恢复。

恢复阶段SOC的估算：

（a）若从放电状态进入恢复状态

SOCt=SOCd+M×t/（8×Q）×100%

式中：SOCt为恢复状态下的荷电状态值；SOCd为放电状态终止时的荷电状态值；M为在电池放电过程中的累积电量（可以恢复）；t为电池在恢复状态下经历的时间；Q为电池的实际容量。

（b）若从充电状态进入恢复状态

SOCt=SOCc+M×t/（8×Q）×100%

式中：SOCt为恢复状态下的荷电状态值；SOCc为充电状态终止时的荷电状态值；M为在电池充电过程中的累积电量（可以恢复）；t为电池在恢复状态下经历的时间；Q为电池的实际容量。

M值的计算：

（a）放电状态下

若η2》η1，

Mt+Δt=Mt+I2×Δt×（1-η2）/η2-I1×Δt×（η2-η1）/η1×η2（1）

推导如下：

t+Δt时刻，安时计量法计算的电量：I2×Δt;

t+Δt 时刻，电池实际放出的电量：I2×Δt/η2;

t+Δt时刻，电池损失电量：I2×Δt ×（1-η2）/η2;

t时刻，I1放电时，由于η2》η1，损失电量I1×Δt×（1-η1）/η1较大，在t+Δt 时刻就会恢复少许电量，恢复量为：

I1×Δt×（1-η1）/η1-I1×Δt×（1-η2）/η2

即I1×Δt ×（η2-η1）/η1×η2

若η1≥η2，t+Δt时刻损失的电量更大，因此就无恢复量I1×Δt ×（η2-η1）/η1×η2.

Mt +Δt=Mt+I2×Δt ×（1-η2）/η2 （2）。

式中：η1、I1为电池在t时刻的放电库仑效率和电流，η2、I2为电池在t +Δt 时刻的放电库仑效率和电流。

（b）充电状态下，充电方式一般为恒流恒压方式，因此库仑效率、电流值的变化较放电状态下稳定。

恒流阶段，电流恒定，而电池温度会有所增加：

M t +Δt=Mt+I×Δt ×（1+η1-2η2）

公式推导同（1）。

式中：I为恒流阶段的电流值；η1、η2为恒流阶段的充电库伦效率，η2》η1，它们的差别是由温度引起的。恒压阶段，电流会随电压的升高而降低。

若η2》η1，Mt +Δt=Mt+I2×Δt×（1-η2）-I1×Δt ×（η2-η1）公式推导同（1）。

若η1≥η2，Mt+Δt=Mt+I2×Δt×（1-η2）公式推导同（2）。

式中：η1、I1为电池在t时刻的充电库仑效率和电流；η2、I2为电池在t +Δt 时刻的充电库仑效率和电流。

在充电情况下，一般用已规定好的电流进行充电，可认为η=1.

1.3 充电或放电状态

1.3.1 安时计量法的改进。

此状态下在SOC估算时一般采用安时计量法，即Q=∫Idt，但这种方法由于没有考虑库仑效率，使得计算结果随着时间的积累误差会越来越大。为此，本文对安时计量法进行了改进，在充放电过程SOC估算中增加了库仑效率因子以及以其为基础计算出的动态恢复电量部分，从而提高了安时计量法的准确性。

改进后的SOC计算公式如下所示：

（a）充电时。

若η2》η1：

等式右边第二项表示实际充入电池的电量部分，第三项表示电池充电过程中动态恢复的电量部分。

若η1≥η2：

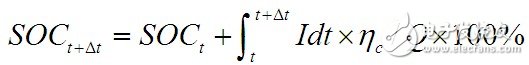
（b）放电时。

若η2》η1：

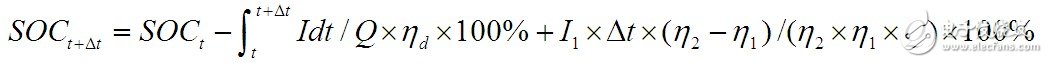
等式右边第二项表示实际放出的电池电量部分，第三项表示电池放电过程中动态恢复的电量部分。

若η1≥η2：

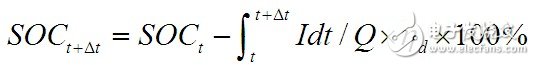
1.3.2 库仑效率η的计算

放电库仑效率定义为电池以特定电流和温度（可以为任意的）进行恒流恒温放电，放完为止，用放出的电量与电池未放电前的电量相比。

充电库仑效率定义为电池在空电量状态下以特定的电流（一般为定义好的）和温度进行充电，充到放电前电量为止，用充入的电量与电池放电前电量相比。

由于内阻及极化现象的存在，电池的充放电过程会有电量的损失，从而造成安时法计算的电量不能完全反映电池充放电真实电量的情况，库仑效率则反映了两者间差别。

传统定义下的库仑效率没有考虑充放电差异、电流大小、运行温度等因素的影响。为了克服传统库仑效率的缺点，本文用神经网络对库仑效率进行估算，因为神经网络具有表示任意非线性关系和学习能力的优点，这样可以得到较为准确的结果。

本文采用自适应模式的神经网络，如图3所示，其结构为输入层两个节点，电流和温度；中间层节点数根据实际情况而定（本文采用19个节点）；一个输出层节点η。采用电流和温度作为输入节点的原因是库仑效率η主要是受其影响，特别是受电流的影响较大。

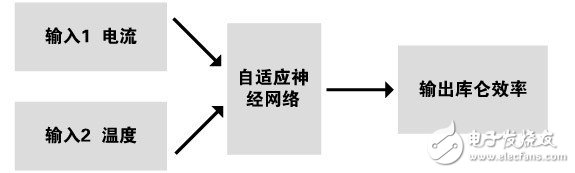
图3 自适应神经网络模型

用神经网络估算库仑效率η的过程是：（1）通过实验获得经验数据；（2）用获得的经验数据对神经网络进行训练；（3）将训练好的神经网络应用于SOC估算中实时估算η。

图4，图5是充放电库仑效率与电流、温度的关系曲线图。图4、5 中连线表示从充放电实验中得出的曲线，“+”表示神经网络估算的结果。

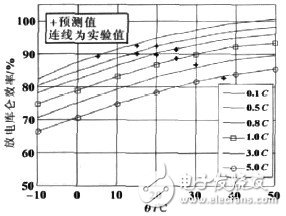
图4 放电库仑效率与电流、温度的关系曲线图

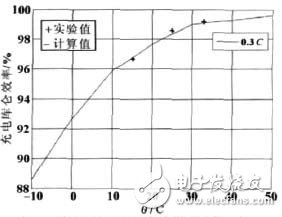
图5 充电库仑效率与电流、温度的关系图

从两图可以看出充放电库仑效率的仿真结果与实验值相符，说明可以用神经网络估算库仑效率η。

最后，锂电池随着充放电次数的增加会逐渐老化，其表现是电池的实际容量会减少，对此可以用公式 ：Q=100×Qch/（SOCsf-SOCsi）对电池的实际容量进行修正。式中：Q表示修正后的实际容量；SOCsf表示充电前在静止状态时的SOC值，SOCsi表示充电后在静止状态时的SOC值；Qch表示在充电状态下充入电池的电量。经过对电池的实际容量的修正将会进一步减少SOC的计算误差，使其更加接近实际值。

2、实验结果

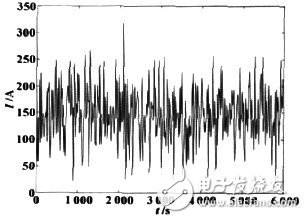
图6 电池工作电流曲线

为了检验此方法的准确性，我们以龙门旅游区旅游用电动车（电池标准容量60Ah）为实验对象。实验前以0.3C的电流向电池充入49.12Ah电量（对应SOC值为0.816），将硬件测试系统（电压、电流、温度传感器精度是0.5%，采样时间为0.5s/次）安装在电动车上，在常规路况下行驶进行试验。试验后用0.1C放出21.61Ah电量（对应SOC为0.358）。图6、图7分别为硬件系统所记录的电池电流、温度曲线图。图8为硬件系统记录的各种SOC估计方法比较，Ah曲线表示安时计量法计算的SOC;Ah-K曲线表示加上库仑效率因子后安时计量法计算的SOC;Ah-K-D表示加上库仑效率因子和电量的动态恢复量后安时计量法计算的SOC.

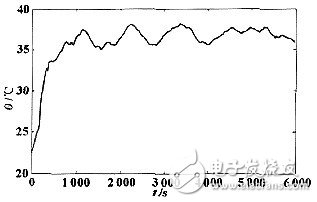
图7 电池工作温度曲线图

实验表明，单纯的安时计量法（Ah法）计算的SOC误差较大，这是因为电池在工作过程中会发生极化现象；经过库仑效率修正后（Ah-K法）可以大大消除极化现象的影响，提高了安时计量法计算SOC的准确度，终止时刻的SOC值接近真实值；在此基础上通过增加电量的动态恢复量（Ah-K-D法）进一步提高了SOC的准确度，终止时刻的SOC值最接近真实值（0.358），从而说明了Ah-K-D 法效果良好。

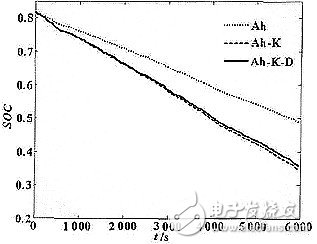
图8 不同SOC 方法计算结果对比图

3、结论

本文在SOC估算上采用了一种新思路，即将锂电池的工作状况分为三个状态，每一状态应用适合其情况的方法估算SOC，从而完成了电池在整个工作过程中的SOC的计算。

此方法最大可能地消除了影响SOC估算的因素，从而提高了SOC估算的精度。文章还特别针对充放电过程中的极化现象以及电池长时间使用所表现出的老化现象提出了改进措施，并产生了较好的效果。经实验表明本文提出的方法易于在嵌入式系统中实现，估算出的SOC 值准确，能够达到动力汽车的应用要求。