

opencv角点检测原理详解
电子常识
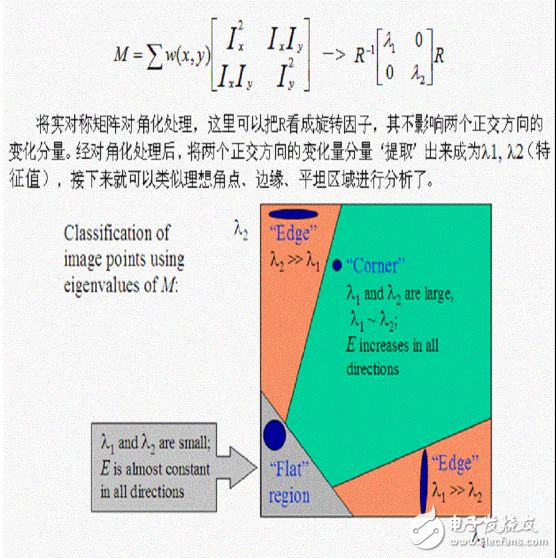
描述
角点:最直观的印象就是在水平、竖直两个方向上变化均较大的点,即Ix、Iy都较大
边缘:仅在水平、或者仅在竖直方向有较大的变化量,即Ix和Iy只有其一较大 平坦地区:在水平、竖直方向的变化量均较小,即Ix、Iy都较小
Harris角点检测算子是于1988年由CHris Harris & Mike Stephens提出来的。在具体展开之前,不得不提一下Moravec早在1981就提出来的Moravec角点检测算子。
1.Moravec角点检测算子
Moravec角点检测算子的思想其实特别简单,在图像上取一个W*W的“滑动窗口”,不断的移动这个窗口并检测窗口中的像素变化情况E。像素变化情况E可简单分为以下三种:A 如果在窗口中的图像是什么平坦的,那么E的变化不大。B 如果在窗口中的图像是一条边,那么在沿这条边滑动时E变化不大,而在沿垂直于这条边的方向滑动窗口时,E的变化会很大。 C 如果在窗口中的图像是一个角点时,窗口沿任何方向移动E的值都会发生很大变化。
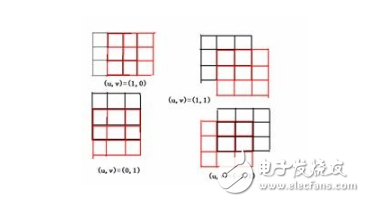
上图就是对Moravec算子的形象描述。用数学语言来表示的话就是:
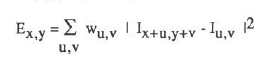
其中(x,y)就表示四个移动方向(1,0)(1,1)(0,1)(-1,1),E就是像素的变化值。Moravec算子对四个方向进行加权求和来确定变化的大小,然和设定阈值,来确定到底是边还是角点。
2.Harris角点检测算子
Harris角点检测算子实质上就是对Moravec算子的改良和优化。在原文中,作者提出了三点Moravec算子的缺陷并且给出了改良方法:
1. Moravec算子对方向的依赖性太强,在上文中我们可以看到,Moravec算子实际上只是移动了四个45度角的离散方向,真正优秀的检测算子应该能考虑到各个现象的移动变化情况。为此,作者采用微分的思想(这里不清楚的话可以复习下高数中的全微分):
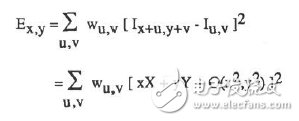
其中:

所以E就可以表示为:
2.由于Moravec算子采用的是方形的windows,因此的E的响应比较容易受到干扰,Harris采用了一个较为平滑的窗口——高斯函数:
3.Moravec算子对边缘响应过于灵敏。为此,Harris提出了对E进行变形:
对,没错,变成了二次型,果然是大牛,更牛的还在后面!其中,
用α,β表示矩阵M的特征值,这样会产生三种情况:A 如果α,β都很小,说明高斯windows中的图像接近平坦。 B 如果一个大一个小,则表示检测到边。 C 如果α,β都很大,那么表示检测到了角点。
α,β表示矩阵M的特征值,这样会产生三种情况:
A.α,β都很小,说明高斯Windows中的图像接近平坦
B.如果一个大一个小,则表示检测到边
C.α,β都很大,那么表示检测到角点。
角点响应
R=det(M)-k*(trace(M)^2) (附录资料给出k=0.04~0.06,opencv指出是0.05-0.5,浮动较大)
det(M)=λ1*λ2 trace(M)=λ1+λ2
R取决于M的特征值,对于角点|R|很大,平坦的区域|R|很小,边缘的R为负值。
算法步骤

其中,局部极大值可用先膨胀后与原图比较的方法求得,具体见二中源码。
opencv代码实现
harris类
#ifndef HARRIS_H
#define HARRIS_H
#include “opencv2/opencv.hpp”
class harris
{
private:
cv::Mat cornerStrength; //opencv harris函数检测结果,也就是每个像素的角点响应函数值
cv::Mat cornerTh; //cornerStrength阈值化的结果
cv::Mat localMax; //局部最大值结果
int neighbourhood; //邻域窗口大小
int aperture;//sobel边缘检测窗口大小(sobel获取各像素点x,y方向的灰度导数)
double k;
double maxStrength;//角点响应函数最大值
double threshold;//阈值除去响应小的值
int nonMaxSize;//这里采用默认的3,就是最大值抑制的邻域窗口大小
cv::Mat kernel;//最大值抑制的核,这里也就是膨胀用到的核
public:
harris():neighbourhood(3),aperture(3),k(0.01),maxStrength(0.0),threshold(0.01),nonMaxSize(3){
};
void setLocalMaxWindowsize(int nonMaxSize){
this-》nonMaxSize = nonMaxSize;
};
//计算角点响应函数以及非最大值抑制
void detect(const cv::Mat &image){
//opencv自带的角点响应函数计算函数
cv::cornerHarris (image,cornerStrength,neighbourhood,aperture,k);
double minStrength;
//计算最大最小响应值
cv::minMaxLoc (cornerStrength,&minStrength,&maxStrength);
cv::Mat dilated;
//默认3*3核膨胀,膨胀之后,除了局部最大值点和原来相同,其它非局部最大值点被
//3*3邻域内的最大值点取代
cv::dilate (cornerStrength,dilated,cv::Mat());
//与原图相比,只剩下和原图值相同的点,这些点都是局部最大值点,保存到localMax
cv::compare(cornerStrength,dilated,localMax,cv::CMP_EQ);
}
//获取角点图
cv::Mat getCornerMap(double qualityLevel) {
cv::Mat cornerMap;
// 根据角点响应最大值计算阈值
threshold= qualityLevel*maxStrength;
cv::threshold(cornerStrength,cornerTh,
threshold,255,cv::THRESH_BINARY);
// 转为8-bit图
cornerTh.convertTo(cornerMap,CV_8U);
// 和局部最大值图与,剩下角点局部最大值图,即:完成非最大值抑制
cv::bitwise_and(cornerMap,localMax,cornerMap);
return cornerMap;
}
void getCorners(std::vector《cv::Point》 &points,
double qualityLevel) {
//获取角点图
cv::Mat cornerMap= getCornerMap(qualityLevel);
// 获取角点
getCorners(points, cornerMap);
}
// 遍历全图,获得角点
void getCorners(std::vector《cv::Point》 &points,
const cv::Mat& cornerMap) {
for( int y = 0; y 《 cornerMap.rows; y++ ) {
const uchar* rowPtr = cornerMap.ptr《uchar》(y);
for( int x = 0; x 《 cornerMap.cols; x++ ) {
// 非零点就是角点
if (rowPtr[x]) {
points.push_back(cv::Point(x,y));
}
}
}
}
//用圈圈标记角点
void drawOnImage(cv::Mat &image,
const std::vector《cv::Point》 &points,
cv::Scalar color= cv::Scalar(255,255,255),
int radius=3, int thickness=2) {
std::vector《cv::Point》::const_iterator it=points.begin();
while (it!=points.end()) {
// 角点处画圈
cv::circle(image,*it,radius,color,thickness);
++it;
}
}
};
#endif // HARRIS_H
相关测试代码:
cv::Mat image, image1 = cv::imread (“test.jpg”);
//灰度变换
cv::cvtColor (image1,image,CV_BGR2GRAY);
// 经典的harris角点方法
harris Harris;
// 计算角点
Harris.detect(image);
//获得角点
std::vector《cv::Point》 pts;
Harris.getCorners(pts,0.01);
// 标记角点
Harris.drawOnImage(image,pts);
cv::namedWindow (“harris”);
cv::imshow (“harris”,image);
cv::waitKey (0);
return 0;
相关测试结果:
改进的Harris角点检测
从经典的Harris角点检测方法不难看出,该算法的稳定性和k有关,而k是个经验值,不好把握,浮动也有可能较大。鉴于此,改进的Harris方法()直接计算出两个特征值,通过比较两个特征值直接分类,这样就不用计算Harris响应函数了。
另一方面,我们不再用非极大值抑制了,而选取容忍距离:容忍距离内只有一个特征点。
该算法首先选取一个具有最大 最小特征值的点(即:max(min(e1,e2)),e1,e2是harris矩阵的特征值)作为角点,然后依次按照最大最小特征值顺序寻找余下的角点,当然和前一角点距离在容忍距离内的新角点呗忽略。
opencv测试该算法代码如下:
cv::Mat image, image1 = cv::imread (“test.jpg”);
//灰度变换
cv::cvtColor (image1,image,CV_BGR2GRAY);
// 改进的harris角点检测方法
std::vector《cv::Point》 corners;
cv::goodFeaturesToTrack(image,corners,
200,
//角点最大数目
0.01,
// 质量等级,这里是0.01*max(min(e1,e2)),e1,e2是harris矩阵的特征值
10);
// 两个角点之间的距离容忍度
harris().drawOnImage(image,corners);//标记角点
测试结果如下:
FAST角点检测
算法原理比较简单,但实时性很强。
该算法的角点定义为:若某像素点圆形邻域圆周上有3/4的点和该像素点不同(编程时不超过某阈值th),则认为该点就是候选角点。opencv更极端,选用半径为3的圆周上(上下左右)四个点,若超过三个点和该像素点不同,则该点为候选角点。
和Harris算法类似,该算法需要非极大值抑制。
opencv代码:
cv::Mat image, image1 = cv::imread (“test.jpg”);
cv::cvtColor (image1,image,CV_BGR2GRAY);
//快速角点检测
std::vector《cv::KeyPoint》 keypoints;
cv::FastFeatureDetector fast(40,true);
fast .detect (image,keypoints);
cv::drawKeypoints (image,keypoints,image,cv::Scalar::all(255),cv::DrawMatchesFlags::DRAW_OVER_OUTIMG);
测试结果如下:
关于矩阵知识的一点补充:好长时间没看过线性代数的话,这一段比较难理解。可以看到M是实对称矩阵,这里简单温习一下实对称矩阵和二次型的一些知识点吧。
1. 关于特征值和特征向量:
特征值的特征向量的概念忘了就自己查吧,这里只说关键的。对于实对称矩阵M(设阶数为n),则一定有n个实特征值,每个特征值对应一组特征向量(这组向量中所有向量共线),不同特征值对应的特征向量间相互正交;(注意这里说的是实对称矩阵,不是所有的矩阵都满足这些条件)
2. 关于对角化:
对角化是指存在一个正交矩阵Q,使得 Q’MQ 能成为一个对角阵(只有对角元素非0),其中Q’是Q的转置(同时也是Q的逆,因为正交矩阵的转置就是其逆)。一个矩阵对角化后得到新矩阵的行列式和矩阵的迹(对角元素之和)均与原矩阵相同。如果M是n阶实对称矩阵,则Q中的第 j 列就是第 j 个特征值对应的一个特征向量(不同列的特征向量两两正交)。
3. 关于二次型:
对于一个n元二次多项式,f(x1,x2.。。.xn) = ∑ ( aij*xi*xj ) ,其中 i 和 j 的求和区间均为 [1,n] ,
可将其各次的系数 aij 写成一个n*n矩阵M,由于 aij 和 aji 的对称等价关系,一般将 aij 和 aji 设为一样的值,均为 xi*xj 的系数的二分之一。这样,矩阵M就是实对称矩阵了。即二次型的矩阵默认都是实对称矩阵
4. 关于二次型的标准化(正交变换法):
二次型的标准化是指通过构造一个n阶可逆矩阵 C,使得向量 ( x1,x2.。.xn ) = C * (y1,y2.。.yn),把n维向量 x 变换成n维向量 y ,并代入f(x1,x2.。。.xn) 后得到 g(y1,y2.。.yn),而后者的表达式中的二次项中不包含任何交叉二次项 yi*yj(全部都是平方项 yi^2),也即表达式g的二次型矩阵N是对角阵。用公式表示一下 f 和 g ,(下面的表达式中 x 和 y都代表向量,x‘ 和 y’ 代表转置)
f = x‘ * M * x ;
g = f = x’ * M * x = (Cy)‘ * M * (Cy) = y’ * (C‘MC) * y = y’ * N * y ;
因此 C‘MC = N。正交变换法,就是直接将M对角化得到N,而N中对角线的元素就是M的特征值。正交变换法中得到的 C 正好是一个正交矩阵,其每一列都是两两正交的单位向量,因此 C 的作用仅仅是将坐标轴旋转(不会有放缩)。
OK,基础知识补充完了,再来说说Harris角点检测中的特征值是怎么回事。这里的 M 是
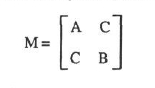
将M对角化后得到矩阵N,他们都是2阶矩阵,且N的对角线元素就是本文中提到的 α 和 β。
本来 E(x,y) = A*x^2 + 2*C*x*y + B*y^2 ,而将其标准后得到新的坐标 xp和yp,这时表达式中就不再含有交叉二次项,新表达式如下:
E(x,y) = Ep (xp,yp) = α*xp^2 + β*yp^2,
我们不妨画出 Ep (xp,yp) = 1 的等高线L ,即
α*xp^2 + β*yp^2 = 1 ,
可见这正好是(xp,yp)空间的一个椭圆,而α 和 β则分别是该椭圆长、短轴平方的倒数(或者反过来),且长短轴的方向也正好是α 和 β对应的特征向量的方向。由于(x,y)空间只是 (xp,yp)空间的旋转,没有放缩,因此等高线L在(x,y)空间也是一个全等的椭圆,只不过可能是倾斜的。
现在就能理解下面的图片中出现的几个椭圆是怎么回事了,图(a)中画的正是高度为 1 的等高线,(其他”高度“处的等高线也是椭圆,只不过长短轴的长度还要乘以一个系数)。其他的几幅图片中可以看到,“平坦”区域由于(高度)变化很慢,等高线(椭圆)就比较大;而”边缘“区域则是在一个轴向上高度变化很快,另一个与之垂直的轴向上高度变化很慢,因此一个轴很长一个轴很短;“角点”区域各个方向高度都变化剧烈,因此椭圆很小。我们人眼可以直观地看到椭圆的大小胖瘦,但如何让计算机识别这三种不同的几何特征呢?为了能区分出角点、边缘和平坦区域我们现在需要用α 和 β构造一个特征表达式,使得这个特征式在三种不同的区域有明显不同的值。一个表现还不错的特征表达式就是:
(αβ) - k(α+β)^2
表达式中的 k 的值怎么选取呢?它一般是一个远小于 1 的系数,opencv的默认推荐值是 0.04(=0.2的平方),它近似地表达了一个阈值:当椭圆短、长轴的平方之比(亦即α 和 β两个特征值之比)小于这个阈值时,认为该椭圆属于“一个轴很长一个轴很短”,即对应的点会被认为是边缘区域。
对于边缘部分,(假设较大的特征值为β)由于 β》》α且α《kβ,因此特征式 :
(αβ) - k(α+β)^2 ≈ αβ - kβ^2 《 (kβ)β - kβ^2 = 0
即边缘部分的特征值小于0 ;
对于非边缘部分,α 和 β相差不大,可认为 (α+β)^2 ≈ 4αβ,因此特征式:
(αβ) - k(α+β)^2 ≈ αβ - 4kαβ = ( 1 - 4k ) * αβ
由于 k 远小于1,因此 1 - 4k ≈ 1,这样特征式进一步近似为:
(αβ) - k(α+β)^2 ≈ αβ
在角点区域,由于α 和 β都较大,对应的特征式的值也就很大;而在平坦区域,特征式的值则很小。
因此,三种不同区域的判别依据就是: 如果特征表达式的值为负,则属于边缘区域;如果特征表达式的值较大,则属于角点区域;如果特征表达式的值很小,则是平坦区域。
最后,由于αβ和(α+β)正好是M对角化后行列式和迹,再结合上面补充的基础知识第2条中提到的行列式和迹在对角化前后不变,就可以得到 (αβ) - k(α+β)^2 = det(M) - k*Tr(M)^2,这就是Harris检测的表达式。
-
一种全新的棋盘角点检测方法2021-03-30 1061
-
《OpenCV3编程入门》角点检测之Shi-Tomasi角点检测2020-05-25 848
-
OpenCV3.1教程之Harris角点检测的详细课件免费下载2020-01-06 851
-
labview中角点检测的函数吗2017-05-24 3962
-
OpenCV3编程入门-源码例程全集-Shi-Tomasi角点检2016-09-18 776
-
【DragonBoard 410c试用体验】 之OpenCV中之图像角点检测实现2016-09-13 12689
-
语音处理检测技术端点检测、降噪和压缩详解2016-08-23 6688
-
Shi-Tomasi角点检测2016-06-06 491
-
机器视觉图像处理之角点检测技术2016-01-22 4303
-
基于FPGA的图像角点检测2012-04-10 4321
-
基于小波变换多尺度Harris角点检测算法2010-01-09 679
全部0条评论

快来发表一下你的评论吧 !

