正态分布和高斯分布的作用_高斯分布的定义_误差服从高斯分布

　　正态分布（Normal distribution），也称“常态分布”，又名高斯分布（Gaussian distribution），最早由A.棣莫弗在求二项分布的渐近公式中得到。C.F.高斯在研究测量误差时从另一个角度导出了它。P.S.拉普拉斯和高斯研究了它的性质。是一个在数学、物理及工程等领域都非常重要的概率分布，在统计学的许多方面有着重大的影响力。

　　正态曲线呈钟型，两头低，中间高，左右对称因其曲线呈钟形，因此人们又经常称之为钟形曲线。

　　若随机变量X服从一个数学期望为μ、方差为σ^2的正态分布，记为N（μ，σ^2）。其概率密度函数为正态分布的期望值μ决定了其位置，其标准差σ决定了分布的幅度。当μ = 0，σ = 1时的正态分布是标准正态分布。

　　

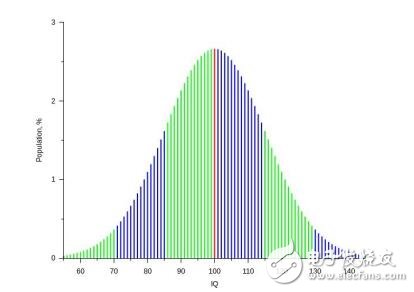
　　高斯分布的定义

　　高斯分布怎么来的，很简单。只要你观察的系统里，各种对象之间关联很弱，那么他们的总和平均表现，根据中心极限定律，就是高斯或者近高斯的。你看我们人造的东西，很多都是模块化的，比如汽车轮船飞机，桌子椅子板凳，等等。我们人类造东西，都是“搭”出来的，一个模块和另一个模块之间关联很弱，坏了一个模块换掉就好。所以人造系统，其表现，包括性能啊，噪声啊，稳定度啊，都基于高斯分布。

　　但自然界呢，假如有个造物主，它造东西跟人类的思路就很不一样。它手里的作品是“生长”出来的。比如我们人，从一个受精卵发育而来，各个部分强关联，受精卵上一点缺陷，会反映到整个人体的巨大影响。这和桌子有本质区别，就算桌子原始材料有个洞，也不可能造出来桌面和桌腿都很多洞。“生长”这个过程到底服从什么本质的数学规律，我们人类还不确切知道。从2000年以后，学界的研究集中于通过随机游动，扩散这样的动力学行为来对“生长”出来的系统（复杂系统）尝试寻找类似于模块系统的中心极限定律的总体规律。有一些进展，但是还没有特别令人信服的突破性结论。

　　高斯分布为何在自然界如此常见高斯分布的信息熵最大。即，高斯分布是最混乱系统。

　　这里有个前提条件是方差一定，这个条件在物理学家的眼中可以意味着涨落，可以是统计学上的能量的涨落（比如maxwell速度矢量分布的方差是确定的kt/m），或者是不确定关系下的涨落。

　　自然会趋向于最熵增和低能量态。这是热力学的最简单运行轨迹。

　　个人认为比之中心极限定理，这个是更为本质的因素。就像我们可以证明出来牛顿力学基础上的经典力学，但是显然是更加优雅和接近自然本质的描述。

　　

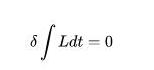
　　高斯分布的作用

　　均匀分布是均匀分布，高斯分布是高斯分布，高斯分布式又名正太分布。均匀分布就是在一个大的区域内，数据出现在任何一个小的区域的概率都是相同的。高斯分布式就是在一个大的区域内，数据会集中出现在部分区域。

　　为什么误差总是服从高斯分布？

　　最近某网友在进行机器学习，发现在对误差假定是都是服从高斯分布，不明白其中缘由。

　　解答如下：

　　1. 大量独立的随机变量之和趋向于某个稳定的分布，这就是中心极限定理。

　　2. 后来人们给这种分布取了个名，叫高斯分布，或正态分布。

　　3. 人们认为误差是随机的，所以人们认为误差的和服从高斯分布。

　　个人认为，一般测量的误差是随机的，但机器学习中的误差是否随机就不一定了。

　　另外还有人认为：

　　不确定误差产生的原因更要用高斯分布来估计了，因为根据中心极限定理，这样做“最无偏”。如果确定了误差产生原因，那就具体情况具体分析了。