PMOS集成变容管高频简化模型的设计

引言

变容管是压控振荡器、调频器、锁相环等电路的关键部件。传统的分立电子线路常采用特制的二极管作为变容管，所用材料多为硅或砷化镓单晶，并采用外延工艺技术。自动频率控制（AFC）和调谐所用的小功率变容二极管通常采用硅的扩散型二极管，也采用合金扩散、外延结合、双重扩散等特殊工艺制作。作为压控器件，这些传统变容二极管的品质因数很小，并且工艺也有特别的要求。这将不便和CMOS工艺兼容从而限制了它在CMOS模拟集成电路中的应用。因而，研究用CMOS工艺制作具有变容特性的MOS管代替一般变容二极管是普通工艺下IC设计很有意义的一项工作。虽然，人们对MOS电容的压控变容特性进行了广泛而深入的研究，但对CMOS工艺集成的PMOS作变容管的研究并不多见。本文针对CMOS工艺下的PMOS压控变容特性进行研究，并对其高频交变压控特性建模，为CMOS工艺兼容高频电路的晶体管级仿真提供简化模型。

1 MOS结构电容的压控特性分析

1．1 理想MIS结构电容的压控特性

根据半导体表面电场效应，通常按照多子堆积状态、多子耗尽状态及少子反型状态3种彼此孤立的理想情况对MIS结构电容的压控特性进行理论分析。但实际上，3种情况间出现过渡过程，如堆积状态与耗尽状态间经过有平带状态、耗尽状态过渡到反型状态经历弱反型直至强反型态，所以其压控特性是连续变化的。倘若交变电压频率较高时，反型层中少子的产生与复合跟不上外电场的变化，其数量基本不变、空间电荷区的电容仍然由耗尽区的电荷变化决定的。因此，在反型区内电容的压控特性有准静态和高频情形之区别，如图1所示。

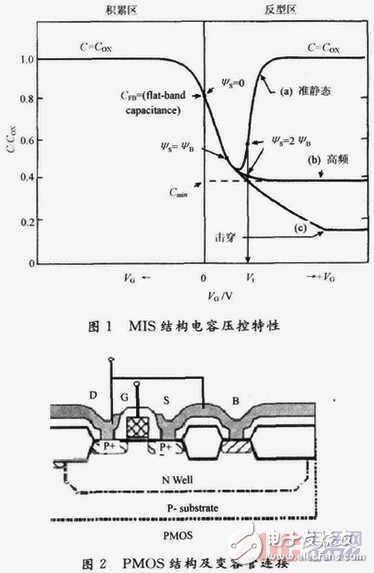
1．2 PMOS的变容管连接及其压控特性分析

图2为PMOS管连接成压控可变电容的示意图。具体是将漏、源和衬底短接作为电容的一极接高电平，栅极作为另一极接低电平。这种连接与MIS电容结构有着类似的机理，所以，电容值随衬底与栅极之间的电压VBG变化。

对于PMOS变容管，在衬栅电压VBG的作用下，变容管的电容可以看作栅氧化层电容与半导体空间电荷区电容的串联，即：

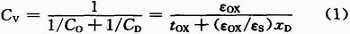
因为反型载流子沟道在VBG超过阈值电压时建立，所以，当VBG远远超越阈值电压时，变容管工作在强反型区域；在栅电位VG大于衬底电位VB时，变容管进入积累区，此时栅氧化层与半导体之间的界面电压为正且足够高使得电子可以自由移动。这样，在反型区和积累区的变容管的电容值：

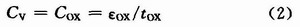
阈值反型点是当达到最大耗尽宽度且反型层电荷密度为零时得到的最小电容：

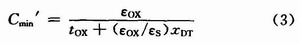
平带是发生在堆积和耗尽模式间，电容为：

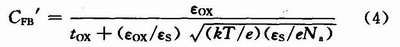
式（1）～式（4）中牵扯到的各参量的意义分别为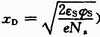：为耗尽层的厚度，εs是半导体的介电常数、φs称为表面势；Na为受主原子的浓度；e为基本电荷的电量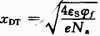；为反型转折点的空间电荷区最大宽度，φf=Vtln（Na／ni）为杂质半导体衬底的相对费米势，Vt= kT／e为热电压，ni为本征载流子浓度，k为玻尔兹曼常数，T为绝对温度；εox为氧化层的介电常数；tox为氧化层厚度。

由于处于耗尽区、弱反型区和中反型区3个区域中的PMOS只有很少的移动载流子，这使得PMOS电容Cv减小（比Cox小）。此时，Cv可以看成由氧化层电容Cox和半导体表面空间电荷层电容（由Cb与Ci的并联电容值，Cb表示耗尽区域电容，而Ci与栅氧化层界面的空穴数量变化相关）串联构成，如式（1）所示。从反型载流子沟道建立开始到强反型区又可细分为3个工作区域：弱反型区、中反型区和强反型区。如果Cb（Ci）占主

导地位，则MOS器件工作在中反型（耗尽）区；如果2个电容都不占主导地位，MOS器件工作在弱反型区。

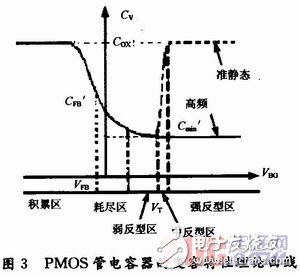
进入强反型区后分为高频和低频两种测试情形，高频条件下少数载流子的产生与复合均跟不上信号的变化，于是Cv不随偏压的变化；而低频（准静态）下它能随偏压而变化。理论上，常常在各区段抓住影响MOS管电容Cv的主要因素进行研究，但各个次要因素与主要因素相互作用，构成连续的变容特性曲线如图3所示。可见，PMOS管电容器的变容特性理论曲线与一般MIS结构电容的特性变化趋势相似。

2 PMOS管变容特性建模与仿真

2．1 PMOS管变容高频特性建模

用HSpice和Candence Spectre进行晶体管级电路模拟仿真时，软件根据晶体管静态条件下所建模型对PMOS变容管准静态特性的获取较为方便，但对其高频特性显得无能为力。以下将基于PMOS变容管准静态特性的基本参数，采用特性曲线拟合的办法，对PMOS变容管高频（即动态）特性进行建模。

由图3可见，Cv随VBG变化的高频特性曲线类似于双曲正切函数曲线，选取曲线的关键点（-∞，Cox）、（VT，Cmin’）并引入电容变化指数γ（类似于变容二极管的结电容变化指数）与此特性曲线进行拟合，得PMOS管高频变容VBG～CV特性的模型函数：

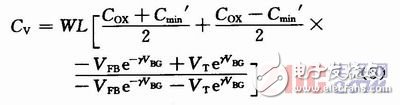
2．2 PMOS管变容特性仿真

2．2．1 变容管准静态特性的Hspice仿真

为获得式（5）中所需的基本参数，且便于和理论分析的特性曲线作对比，选取Charted 0．35μm工艺库，用Hspiee对PMOS管连接的变容器与以固定电容器相串联，离散加入一系列静态偏压，根据分压逐一地得到PMOS变容器的容值和对应的偏压。仿真时，PMOS管尺寸取L=1μ，W=7．1μm，得到逐点仿真的准静态拟合曲线如图4所示。

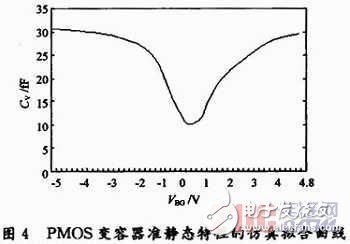
这个曲线的走势与理论分析的变化趋势一致。

2．2．2 变容管高频特性的Matlab仿真

取L=1μm，分别对W=7．1μm，W=4．3 μm两种情形用Matlab仿真。其他参数为：εs=11.7×8．854×10-12F／m，γ=1／2，VFB=-1．95V，Na=5×1021m-3，ni=1.5×1014m-3，tox=7.46×10-9m，绝对温度T为300K，VT=-0.8427V，e为基本电荷的电量；εox=3.9×8.854×10-12 F／m。仿真得到的PMOS变容器高频特性VBG—CV曲线如图5所示。可见，不同尺寸的PMOS变容管，其最大、最小电容有别，随WL的增大二者均有所增大，相当于极板正对面积增大。这就是设计中确定变容范围的依据。

2．2．3 变容特性仿真结果的对比

为了说明所建模型的正确性，将尺寸为L=1 μm，W=7．1μm的PMOS管用HSpice仿真的准静态变容特性曲线与用Matlab分别仿真L=1μm时W=

7．1μm，W=4．3 μm的高频变容特性曲线放在同一VBG—CV坐标上比较，如图6所示。

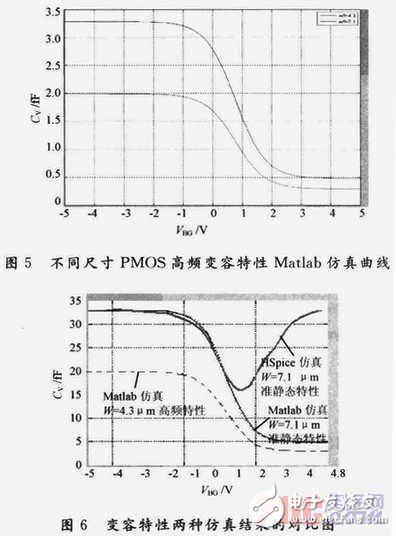
可见，PMOS变容特性在准静态与高频特性分离以前曲线吻合得很好。由于HSpiee仿真与具体工艺参数相结合，可以认为仿真曲线为实际准静态特性，而用Matlab对高频模型仿真所得到的高频变容特性曲线为模型曲线。并且二者共同完成了对PMOS电容器连接的变容特性描述，其结果和分析结果与图2一致。

3 结语

本文对PMOS用作变容管时的特性进行了研究，用HSpice对准静态特性进行仿真描绘，从而确定了一些关键点。在此基础上，建立了高频变容特性的简化模型，用Matlab对模型进行了仿真，并与HSpice得到的准静态结果局部比对、与理论分析总体比对均说明了结果的正确性。

该模型补充了与CMOS工艺兼容的变容管设计时在高频情况下的仿真问题；它能够描述管子压控变容显著区段的变化规律。此模型算法可以嵌入到仿真工具里，较为准确地反映控制电压信号的频率在10 kHz以上变容管特性；针对不同的CMOS工艺，修改变容指数即可，因而，此模型有普遍的适用性和较强的移植性。