

拉普拉斯变换及其逆变换表拉普拉斯变换及其逆变换表
电子常识
2681人已加入
描述
拉普拉斯变换应用领域定理
有些情形下一个实变量函数在实数域中进行一些运算并不容易,但若将实变量函数作拉普拉斯变换,并在复数域中作各种运算,再将运算结果作拉普拉斯反变换来求得实数域中的相应结果,
在经典控制理论中,对控制系统的分析和综合,都是建立在拉普拉斯变换的基础上的。引入拉普拉斯变换的一个主要优点,是可采用传递函数代替常系数微分方程来描述系统的特性。这就为采用直观和简便的图解方法来确定控制系统的整个特性、分析控制系统的运动过程,以及提供控制系统调整的可能性。
应用拉普拉斯变换解常变量齐次微分方程,可以将微分方程化为代数方程,使问题得以解决。在工程学上,拉普拉斯变换的重大意义在于:将一个信号从时域上,转换为复频域(s域)上来表示;在线性系统,控制自动化上都有广泛的应用。
拉普拉斯变换及其反变换表
1.表A-1 拉氏变换的基本性质
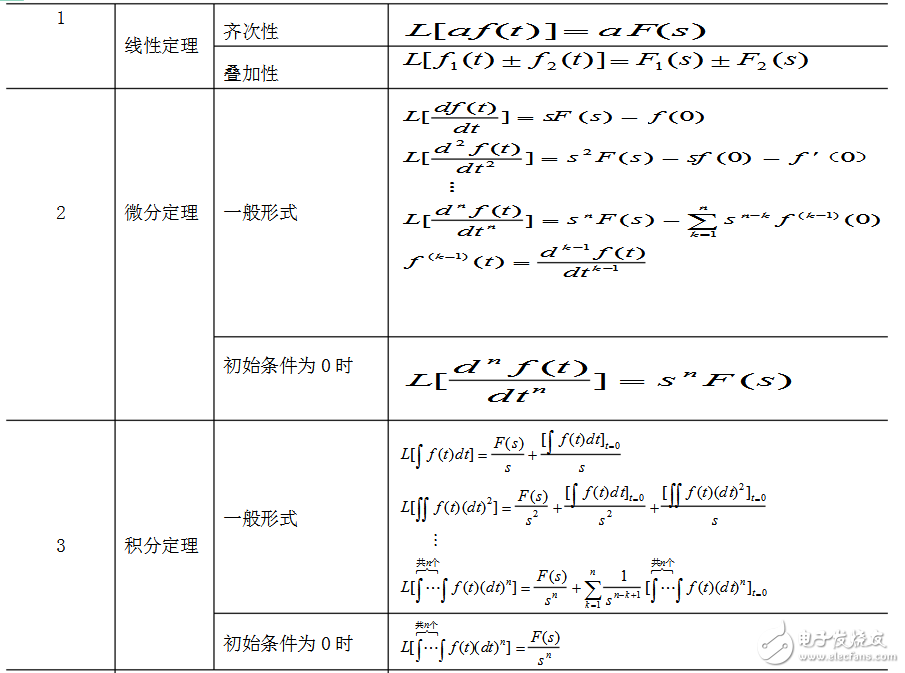

2.表A-2 常用函数的拉氏变换和z变换表
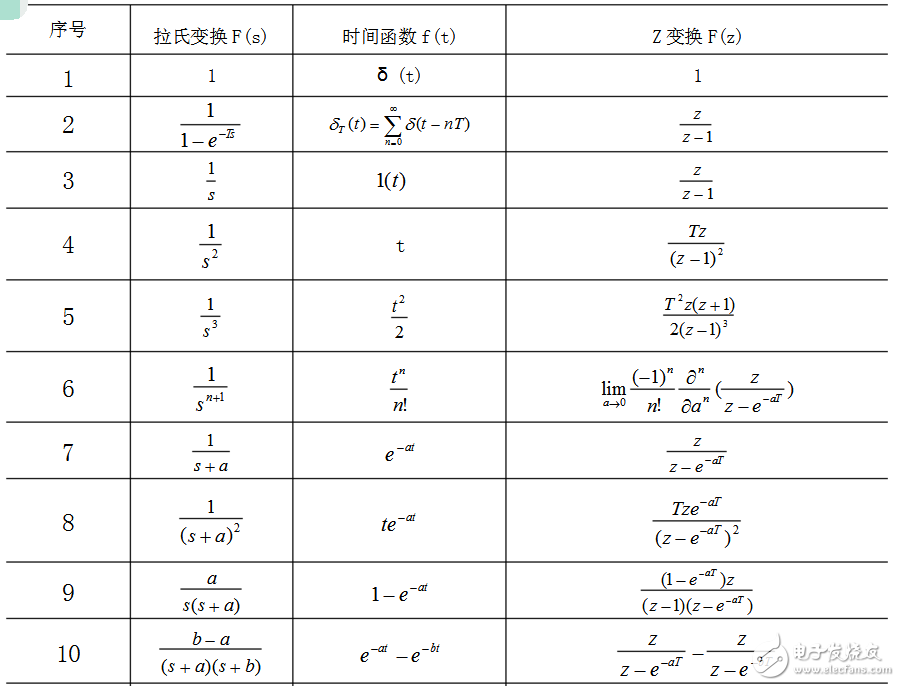
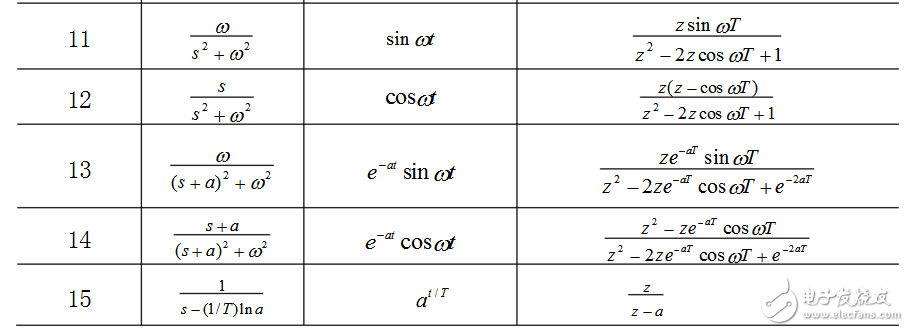
3. 用查表法进行拉氏反变换
用查表法进行拉氏反变换的关键在于将变换式进行部分分式展开,然后逐项查表进行反变换。设F(s)是s的有理真分式
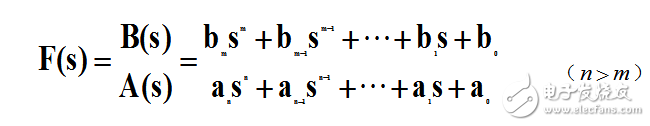
式中系数a,a,。。。,a,a,b,b,。。.b,b都是实常数;nm,是正整数。按代数定理可将F(s)展开为部分分式。分以下两种情况讨论。
① A(s)=0无重根
这时,F(s)可展开为n个简单的部分分式之和的形式。

② A(s)=0有重根
设A(s)=0有r重根1s,F(s)可写为

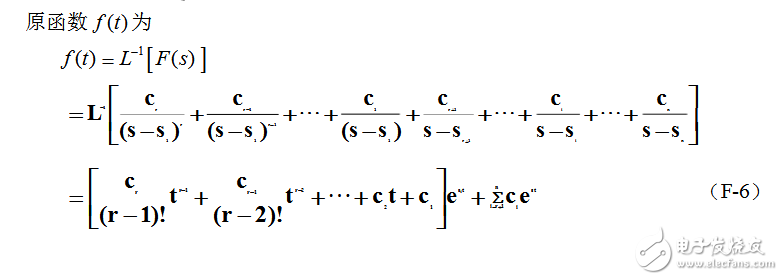
声明:本文内容及配图由入驻作者撰写或者入驻合作网站授权转载。文章观点仅代表作者本人,不代表电子发烧友网立场。文章及其配图仅供工程师学习之用,如有内容侵权或者其他违规问题,请联系本站处理。
举报投诉
-
拉普拉斯变换表下载2021-12-30 1008
-
从傅里叶变换如何推换出拉普拉斯变换?2021-06-23 8372
-
拉普拉斯变换在现代控制领域有哪些应用?2021-04-29 2665
-
计算机Fortran编程实现偏微分方程拉普拉斯变换2020-08-14 3418
-
拉普拉斯变换及其应用_elecfans.com2015-10-28 1295
-
拉普拉斯变换与傅里叶变换的关系.ppt2009-09-16 4750
-
拉普拉斯变换视频教程2009-09-03 6972
-
拉普拉斯变换2009-07-27 6126
-
拉普拉斯变换课件教案2009-07-09 681
-
什么是拉普拉斯变换2009-07-08 7463
全部0条评论

快来发表一下你的评论吧 !

