

拉普拉斯变换与傅里叶变换有什么关系吗
电子常识
描述
傅里叶变换
一种积分变换,它来源于函数的傅里叶积分表示。积分 (1) 称为ƒ 的傅里叶积分。周期函数在一定条件下可以展成傅里叶级数,而在(-∞,∞)上定义的非周期函数ƒ,显然不能用三角级数来表示。但是J.-B.-J.傅里叶建议把ƒ表示成所谓傅里叶积分的方法。
傅里叶变换在物理学、电子类学科、数论、组合数学、信号处理、概率论、统计学、密码学、声学、光学、海洋学、结构动力学等领域都有着广泛的应用(例如在信号处理中,傅里叶变换的典型用途是将信号分解成幅值谱——显示与频率对应的幅值大小)。
拉普拉斯变换
拉普拉斯变换是工程数学中常用的一种积分变换,又名拉氏变换。拉氏变换是一个线性变换,可将一个有参数实数t(t≥ 0)的函数转换为一个参数为复数s的函数。拉普拉斯变换在许多工程技术和科学研究领域中有着广泛的应用,特别是在力学系统、电学系统、自动控制系统、可靠性系统以及随机服务系统等系统科学中都起着重要作用。
有些情形下一个实变量函数在实数域中进行一些运算并不容易,但若将实变量函数作拉普拉斯变换,并在复数域中作各种运算,再将运算结果作拉普拉斯反变换来求得实数域中的相应结果,
在经典控制理论中,对控制系统的分析和综合,都是建立在拉普拉斯变换的基础上的。引入拉普拉斯变换的一个主要优点,是可采用传递函数代替常系数微分方程来描述系统的特性。这就为采用直观和简便的图解方法来确定控制系统的整个特性、分析控制系统的运动过程,以及提供控制系统调整的可能性。
应用拉普拉斯变换解常变量齐次微分方程,可以将微分方程化为代数方程,使问题得以解决。在工程学上,拉普拉斯变换的重大意义在于:将一个信号从时域上,转换为复频域(s域)上来表示;在线性系统,控制自动化上都有广泛的应用。
傅里叶变换与拉普拉斯变换的区别与联系
1、 傅里叶变换与拉普拉斯变换都属于积分变换,是两种常见的数学变换手段,而所谓的积分变换就是通过积分运算,把一个函数变成另一个函数的变换,其作用就是将复杂的函数运算变成简单的函数运算,当选取不同的积分域和变换核时,就得到不同名称的积分变换,傅里叶变换与拉普拉斯变换就是因取不同的积分域与变换核得来的。
2、 傅里叶变换是拉普拉斯变换的特例。拉普拉斯变换是将时域信号变换到“复频域”,与变换的“频域”有所区别。 拉普拉斯变换主要用于电路分析,作为解微分方程的强有力工具(将微积分运算转化为乘除运算)。傅里叶变换则随着FFT算法的发展已经成为最重要的数学工具应用于数字信号处理领域。
傅里叶变换与拉普拉斯变换两种变换的性质有许多相似之处,故两者在求解问题时也会有许多类似,另外,由于傅氏变换的积分区间为(-,),拉氏变换的积分区间为,),两者又会在不同的领域中有着各自的应用。下面通过一些具体的例子来对两种变换的应用做一些研究:
两种积分变换在求解积分、微分方程中的应用 例1 求解积分方程


同样,应用拉普拉斯变换的卷积性质也可以用来求解积分方程。

此即原积分方程的解。 例3 求解线性方程组


两种积分变换在电路理论中的应用

代入数值,化简为i‘(t)-i(t)=-e-t该方程是一阶非齐次线性微分方程,用高等数学的知识进行求解的话,要先求出与之对应的齐次方程的通解与非齐次方程的一个特解。求解步骤比较繁琐,这里我们先采用傅里叶变换法进行求解。
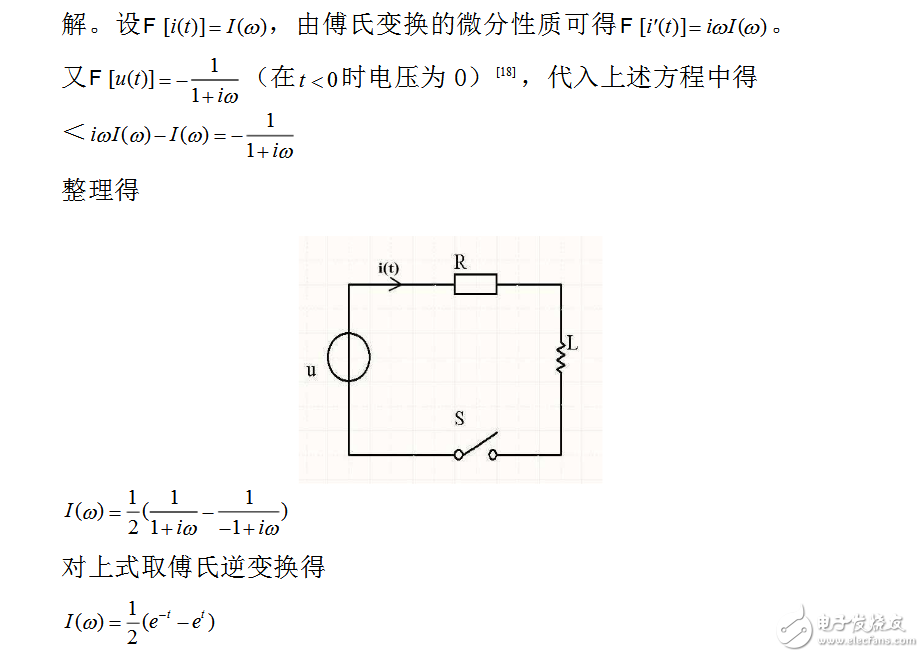
此即电路中的电流。


《信号与系统》、《电路分析》等课程中常常会碰到各种信号的问题,一般来说傅里叶变换法适用于对连续时间系统的分析,这种方法也被称为频域分析法;而拉普拉斯变换法被称为系统的复频域分析[19],这种方法的适用范围更加广泛,以致于在相当长的时期内,人们几乎无法把电路理论与拉普拉斯变换分开来讨论。下面我们再举两个用拉氏变换法解决电路问题的例子: 例5 如图所示,电路为完全耦合互感电路,互感量
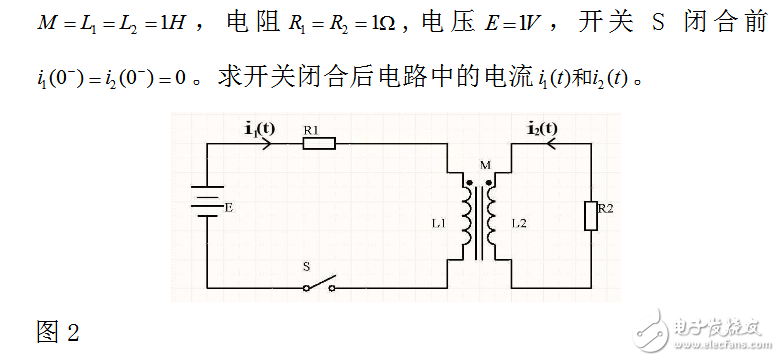
解:由基尔霍夫电压定律可列出电路的微分方程如下:


推广应用
傅里叶变换在物理学、数论、组合数学、信号处理、概率论、统计学、密码学、声学、光学、海洋学、结构力学等领域都有着广泛的应用,例如在信号处理中,傅里叶变换的典型用途是将信号分解成幅值分量和频率分量应用拉普拉斯变换解常变量齐次微分方程,可以将微分方程化为代数方程,是问题得以解决。在工程学上拉普拉斯的重大意义在于将一个信号从时域上转换为复频域上来表示,在线性系统,控制自动化上都有广泛的应用。
-
 jf_68570777
2023-03-17
0 回复 举报牛 收起回复
jf_68570777
2023-03-17
0 回复 举报牛 收起回复
-
 小游民123
2018-11-18
0 回复 举报啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊 收起回复
小游民123
2018-11-18
0 回复 举报啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊 收起回复
-
傅里叶变换和拉普拉斯变换的关系是什么2024-02-18 3781
-
傅里叶变换和拉普拉斯变换的区别联系2023-09-07 4607
-
傅里叶变换、拉普拉斯变换、Z变换剖析2022-11-28 4528
-
从傅里叶变换如何推换出拉普拉斯变换?2021-06-23 8344
-
傅里叶变换与拉普拉斯变换的物理解释及区别pdf文档资料【下载】2017-12-19 1090
-
拉普拉斯、傅里叶及各种变换的原理和意义2017-10-24 7813
-
拉普拉斯变换及其应用_elecfans.com2015-10-28 1292
-
z变换与拉普拉斯变换的关系2009-09-30 1487
-
拉普拉斯变换与傅里叶变换的关系.ppt2009-09-16 4749
-
拉普拉斯变换的基本定理2009-07-27 26427
-
拉普拉斯变换课件教案2009-07-09 680
-
什么是拉普拉斯变换2009-07-08 7442
全部0条评论

快来发表一下你的评论吧 !

